Line Integrals of Scalar Functions (Introduction)

Houston Math Prep

7 May 202025:28

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the concept of line integrals, a fundamental topic in multivariable calculus, explaining their difference from single and multiple integrals. It illustrates how line integrals can be applied to scalar and vector functions over curves in 2D and 3D spaces for various practical applications, such as calculating work, mass of a wire, or surface area. The script provides step-by-step examples of calculating line integrals, including parameterizing curves and integrating over them, with a focus on clarity and understanding.

Takeaways

📚 The script introduces the concept of line integrals, explaining how they differ from single variable and multiple integrals by integrating over a curve in two or three-dimensional space.
🚀 Line integrals can be used for various applications such as calculating work done to put a satellite in orbit, finding the mass of a wire in 3D space, evaluating surface areas, and determining voltage generated around a loop.
📈 The script explains how to calculate line integrals of scalar functions over a curve, using the example of finding the area under a 'curtain' formed by a paraboloid-shaped function above a curve in the XY plane.
📉 The process of integrating over a curve involves parameterizing the curve with a vector-valued function, which is essential for quantifying the curve and setting up the line integral.
🔍 The script demonstrates the calculation of a line integral using the example of the area under an elliptical paraboloid above a circle, showing the steps of parameterizing the curve and evaluating the integral.
📐 The importance of the arc length element (ds) is highlighted, which is used in the integral to represent an infinitesimally small section of the curve.
🔢 The script provides an example of calculating the line integral of a function over a parabola and a straight line, showing how to break down the problem into two separate integrals and parameterize each curve segment.
🌀 An example of a line integral in three-dimensional space is given, using a helix and a scalar function, to illustrate the process of parameterizing the curve and finding the magnitude of the derivative of the parameterization.
📝 The script emphasizes the use of trigonometric identities and double-angle formulas in simplifying and integrating the expressions that arise in line integrals.
🔑 The final takeaway is an encouragement to watch the next part of the video series, which will cover line integrals using vector fields, indicating that this is a continuation of a broader topic.

Q & A

What is the main topic of the video script?
-The main topic of the video script is the introduction to line integrals, explaining what they are and how to calculate them using both scalar functions and vector fields.
What is the difference between a line integral and other types of integrals?
-A line integral integrates a scalar or vector function over a curve in two or three-dimensional space, unlike regular integrals which are over the real line, and iterated or multiple integrals which are over a region in two or three-dimensional space.
Why are line integrals useful in practical applications?
-Line integrals are useful for finding work required to put a satellite in orbit, calculating the mass of a wire curving through space, evaluating the surface area under a curve, calculating voltage generated around a loop, and finding average temperature along a path, among other applications.
How is the area under a curve represented in the context of line integrals?
-The area under a curve in the context of line integrals is represented as the integral of the function f(x, y) with respect to ds, where ds is an infinitesimally small arc length along the curve.
What is the significance of parameterizing a curve in line integrals?
-Parameterizing a curve in line integrals allows us to express the curve as a vector-valued function, which is necessary for calculating the derivative of the curve and the magnitude of that derivative, both of which are used in the line integral formula.
What is the formula for the magnitude of the derivative of a vector-valued function?
-The magnitude of the derivative of a vector-valued function is the square root of the sum of the squares of each component of the derivative vector.
How is the line integral of a scalar function over a curve calculated?
-The line integral of a scalar function over a curve is calculated by substituting the parameterized curve into the scalar function, multiplying by the magnitude of the derivative of the parameterized curve, and integrating over the parameter's bounds.
What is the significance of the double angle formula in the script's example of integrating a function over a circle?
-The double angle formula is used to simplify the integration of a function involving cosine squared T and sine squared T, by combining them into a single term involving cosine of double the angle, which is easier to integrate.
Can you provide an example of a line integral calculation from the script?
-One example from the script is the line integral of 2x squared plus y squared over a counterclockwise path over a circle of radius 2 centered at the origin. The curve is parameterized, and the integral is calculated by substituting the parameterized values into the function, finding the magnitude of the derivative, and integrating over the parameter's bounds from 0 to 2π.
What is the final example in the script about?
-The final example in the script is about calculating a line integral in three-dimensional space using a helix curve. The integral involves the function Y - Z, and the calculation includes the parameterization of the curve, finding the derivative, and integrating over the parameter's bounds.

Outlines

00:00

📚 Introduction to Line Integrals with Scalar Functions

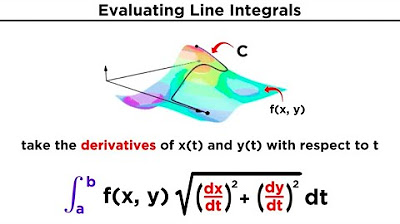
This paragraph introduces the concept of line integrals, distinguishing them from traditional integrals over a real line or in multivariable spaces. The focus is on integrating scalar or vector functions over a curve in two or three-dimensional space, which can be used for various applications, such as calculating work, mass of a wire, surface area, voltage, and temperature along a path. The paragraph explains the process of integrating over a curve by parameterizing it and using arc length as the differential element, setting the stage for calculating line integrals of scalar functions over a curve defined in two-dimensional space.

05:00

📘 Calculating Line Integrals of Scalar Functions

The second paragraph delves into the specifics of calculating line integrals of scalar functions over a curve. Using the example of a circular path, the script explains how to parameterize the curve, substitute values into the function, and calculate the magnitude of the derivative of the parameterization. The process involves setting up the integral with the correct bounds and integrating the function multiplied by the magnitude of the derivative of the parameterization. The example concludes with the integration of an elliptical paraboloid over a circle, demonstrating the practical application of line integrals.

10:01

📙 Line Integrals with Parameterized Curves

This paragraph continues the discussion on line integrals, focusing on the parameterization of curves for the purpose of integration. It provides a step-by-step guide on how to parameterize a parabolic curve and a straight line in two-dimensional space, emphasizing the importance of defining appropriate bounds for the parameter 't'. The paragraph illustrates the process of finding the derivative of the parameterization to calculate the magnitude needed for the line integral. It also sets up the integral for both curves, showing how to substitute the parameterized values into the function and prepare for integration.

15:03

📒 Solving Line Integrals with U-Substitution

The fourth paragraph demonstrates the method of solving line integrals using u-substitution, a common technique in calculus. It applies this method to the first curve of the example, which involves integrating a function along a parabola. The paragraph shows the transformation of the integral into a new variable 'u', simplification, and the application of the power rule to find the antiderivative. The process concludes with evaluating the integral over the specified bounds and combining the results to find the total line integral for the curve.

20:05

📕 Evaluating Line Integrals in Three-Dimensional Space

This paragraph extends the concept of line integrals to three-dimensional space, using the example of a helical curve. It explains the process of parameterizing the curve with its x, y, and z components and emphasizes the need to calculate the derivative of the parameterization to find the magnitude for the integral. The paragraph details the integration of a scalar function over the curve, including the setup of the integral with the correct bounds and the function, and concludes with the evaluation of the integral to find the line integral's value.

25:08

📔 Conclusion and Preview of Vector Field Line Integrals

The final paragraph wraps up the introduction to line integrals with scalar functions and provides a preview of the next topic in the video series, which is line integrals using vector fields. It highlights the difference between scalar and vector field line integrals and encourages viewers to continue watching the series for further exploration of this topic. The paragraph serves as a transition, summarizing the content covered and setting the stage for more advanced material.

Mindmap

Keywords

💡Line Integrals

Line integrals are a fundamental concept in calculus that extend the idea of integration from a single variable to a function defined along a curve in two or three-dimensional space. In the video, line integrals are introduced as a means to integrate scalar or vector functions over a curve, which is essential for calculating quantities like work, mass of a wire, surface area, or voltage. Examples from the script include finding the area under a curve shaped like a paraboloid and the work required to move an object along a path.

💡Scalar Function

A scalar function is a mathematical function that maps input values to a single output value, typically representing a quantity without direction. In the context of the video, the line integral of a scalar function over a curve is used to calculate the area under a curve or the work done along a path. An example given is the line integral of '2x^2 + y^2' over a circular path.

💡Vector Field

A vector field is a concept in physics and mathematics where each point in space is associated with a vector, which has both magnitude and direction. The video mentions that line integrals can also be applied to vector fields, which is a more complex scenario than scalar functions and involves integrating over the direction as well as the magnitude of the vector at each point along the curve.

💡Parameterization

Parameterization is the process of expressing the coordinates of a curve as functions of a single parameter, typically denoted as 't'. It is essential in calculating line integrals because it allows the curve to be described by a formula that can be differentiated and integrated. The script provides examples of parameterizing a circle and a parabola for the purpose of evaluating line integrals.

💡Arc Length

Arc length is the measure of the distance between two points along a curve. In the video, the concept of arc length is related to line integrals through the parameterization of a curve, where the derivative of the parameterized curve is used to find the arc length and subsequently the differential arc length 'ds', which is integral to the line integral formula.

💡Magnitude

The magnitude of a vector is its length, which is a scalar quantity. In the context of line integrals, the magnitude of the derivative of the parameterized curve (R'(t)) is used to find the differential arc length 'ds', which is then used in the line integral formula. The video script mentions finding the magnitude of R'(t) for both a circular path and a straight line path.

💡Double Angle Formula

The double angle formula is a trigonometric identity used to express trigonometric functions of double an angle in terms of functions of the original angle. In the script, the double angle formula is used to simplify the integration of a function involving cosine squared and sine squared of a variable, which is part of the process of evaluating a line integral.

💡U-Substitution

U-substitution is a technique used in integral calculus to simplify the integration of composite functions. In the video, u-substitution is mentioned as a method to evaluate a line integral involving a square root of a quadratic expression, making the integration process more manageable.

💡Three-Dimensional Space

Three-dimensional space refers to a geometric setting where every point is determined by three coordinates, typically x, y, and z. The video script includes an example of a line integral in three-dimensional space involving a helix, demonstrating how line integrals can be applied in more complex spatial scenarios.

💡Helix

A helix is a three-dimensional curve that coils around a cylinder like a spring. In the video, a helical path is used as an example for a line integral in three-dimensional space, illustrating how to integrate a scalar function over a curve that has a non-planar trajectory.

Highlights

Introduction to line integrals and their distinction from single and multivariable integrals.

Explanation of line integrals over curves in two or three-dimensional space.

Use of line integrals in practical applications such as calculating work, mass of a wire, surface area, voltage, and temperature.

Concept of integrating a scalar function over a curve defined by a paraboloid-shaped function.

Approach to finding the area of a curtain using line integrals and the analogy to Riemann sums.

Parameterization of a curve as a vector-valued function for line integral calculations.

Integration of a scalar function over a curve using the arc length element and the parameterized curve.

Example calculation of the area under a curve using line integrals and the elliptical paraboloid function.

Demonstration of parameterizing a circle for line integral calculations and the bounds for a complete traversal.

Calculation of the magnitude of the derivative of a parameterized curve for use in line integrals.

Integration of a scalar function over a parameterized curve using the formula involving the magnitude of the derivative.

Use of double angle formulas in integrating even powers of sine and cosine in line integrals.

Evaluation of line integrals over a parabola and a straight line, involving separate integrals for each curve segment.

Parameterization of a helix in three-dimensional space for a line integral involving a scalar function.

Calculation of the magnitude of the derivative of a parameterized helix for use in a three-dimensional line integral.

Integration of a scalar function over a helix, showcasing the process in three-dimensional space.

Introduction to the next part of the series, focusing on line integrals using vector fields.

Transcripts

Browse More Related Video

Calculus 3: Line Integrals (Video #28) | Math with Professor V

Calculus 3: Green's Theorem (Video #30) | Math with Professor V

Line Integrals of Vector Fields (Introduction)

Conservative Vector Fields & Potential Functions

Calculus 3: Lecture 14.6 Triple Integrals and Applications

Evaluating Line Integrals

Related Tags

Line Integrals Scalar Functions Vector Fields Calculus Concepts Multivariable Calculus Integral Calculation Mathematical Analysis Curve Parameterization Space Geometry Educational Content