Line Integrals of Vector Fields (Introduction)
TLDRIn this Houston Math Prep video, the concept of line integrals over vector fields is introduced and explained. The video illustrates how to calculate the work done by a vector field on a moving object along a curve, using the dot product of the vector field and the unit tangent vector. It covers three common notations for line integrals and demonstrates the process with examples, including calculating the work done by a vector field on a parabola and a 3D curve. The examples show the step-by-step integration process, highlighting the importance of parameterization and simplification in solving such problems.
Takeaways
- 📚 The video introduces line integrals over vector fields, explaining how to calculate the work done by a vector field on an object moving along a curve.
- 📐 It describes the importance of the unit tangent vector in determining the component of the vector field in the direction of the curve.
- 🔍 The script explains the dot product of the vector field and the unit tangent vector as the key to finding the force component along the curve.
- 📈 The magnitude of the vector field times the cosine of the angle between the vectors gives the horizontal component, which is crucial for line integral calculations.
- 🛠 The process of calculating work done by the vector field involves integrating the dot product of the vector field and the unit tangent vector over the curve from point A to B.
- 📝 Three common notations for line integrals of vector fields are introduced, emphasizing their equivalence and interchangeable use in calculations.
- 🧩 The first example involves calculating the line integral of a vector field over a parabola, parameterizing the curve and using the differential form to find the work done.
- 📉 In the second example, a 3D vector field is integrated over a parameterized curve, demonstrating the application of the process in three-dimensional space.
- 📚 The video script provides step-by-step instructions for setting up and solving the integrals, including parameterizing the curve and identifying the components of the vector field.
- 📈 The examples illustrate the simplification process, where the magnitude of the unit tangent vector is considered and the integral is evaluated within the given bounds.
- 🔑 The takeaway emphasizes the practical application of line integrals in physics, particularly in calculating work done by forces in a vector field.
Q & A
What is the main topic of the video?
-The main topic of the video is line integrals over vector fields, explaining how to calculate them and their applications.
What is a line integral of a vector field on a curve?
-A line integral of a vector field on a curve is a way to calculate the work done by a vector field (like forces) on an object as it moves along a curve in space.
What is the role of the unit tangent vector in the context of line integrals?
-The unit tangent vector is used to determine the component of the vector field that is in the direction of the curve's tangent, which is essential for calculating the line integral.
How is the component of the vector field F in the direction of the unit tangent vector found?
-The component is found by taking the dot product of the vector field F and the unit tangent vector, which is represented as F dot T.
Why is the dot product of two vectors related to the cosine of the angle between them?
-The dot product is equal to the product of the magnitudes of the two vectors and the cosine of the angle between them, which is a geometric interpretation of the angle between vectors.
What is the significance of the magnitude of the unit tangent vector being 1 in the context of the dot product?
-Since the unit tangent vector has a magnitude of 1, the dot product simplifies to the magnitude of the vector field F times the cosine of the angle theta, making the calculation of the line integral more straightforward.
What are the three common notations for line integrals of vector fields mentioned in the video?
-The three common notations are: 1) Integral over the curve of F dot T hat dS, 2) Integral over the curve of F dot dR, and 3) Integral over the curve of M dx + N dy (in 2D) or M dx + N dy + P dz (in 3D).
How is the work done by a vector field F on an object moving along a curve C calculated?
-The work is calculated by integrating the dot product of the vector field F and the unit tangent vector along the curve C from point A to B.
What is the process of parameterizing a curve in the context of line integrals?
-Parameterizing a curve involves expressing the curve in terms of a parameter, usually denoted as 't', which allows for the calculation of derivatives and integrals along the curve.
Can you provide an example of how to set up a line integral for a vector field over a parameterized curve?
-Sure, for a vector field F = (M, N, P) and a parameterized curve R(t), you would calculate M dx + N dy + P dz by finding the derivatives dx/dt, dy/dt, and dz/dt, and then integrating M(dx/dt) + N(dy/dt) + P(dz/dt) with respect to t over the given bounds.
Outlines
📚 Introduction to Line Integrals Over Vector Fields
This paragraph introduces the concept of line integrals over vector fields. It explains how a line integral represents the work done by a vector field on an object moving along a curve. The paragraph illustrates the idea with a sketch of a curve and a vector field with vectors pointing in various directions. It also introduces the concept of a unit tangent vector and how the component of the vector field in the direction of the unit tangent vector is found using the dot product. The paragraph concludes by explaining the three common notations used for line integrals of vector fields and how they are equivalent.
🔍 Calculating Line Integrals with Examples
This paragraph delves into the process of calculating line integrals with two detailed examples. The first example involves a vector field and a curve defined by a parabola, where the task is to find the line integral from the origin to a specific point. The paragraph explains how to parameterize the curve, substitute the parameters into the vector field components, and set up the integral using the differential form. The second example extends the concept to 3D space, where the vector field and a parameterized curve are given, and the line integral is calculated similarly. The paragraph emphasizes understanding the components of the vector field in terms of the parameterized curve and the importance of the differentials in the calculation.
🚀 Conclusion and Future Topics on Line Integrals
The final paragraph wraps up the discussion on line integrals over vector fields and teases upcoming topics. It summarizes the process of calculating line integrals and their applications, such as finding work done by a vector field. The paragraph also mentions that future videos will cover more on circulation and flux, indicating a continuation of the topic in subsequent educational content. The speaker thanks the viewers for watching and looks forward to the next video, creating a sense of anticipation for further learning.
Mindmap
Keywords
💡Line Integrals
💡Vector Fields
💡Unit Tangent Vector
💡Dot Product
💡Magnitude
💡Work
💡Parameterization
💡Differential Form
💡Integration
💡Bounds
💡3D Space
Highlights
Introduction to line integrals over vector fields, explaining the concept of integrating a vector field along a curve.
Visualizing a vector field with forces around a curve and the role of the unit tangent vector in line integrals.
The secret revealed: the component of the vector field F in the direction of the unit tangent is given by the dot product F dot T.
Explanation of the dot product formula and its relation to the magnitude and angle between vectors.
Understanding the horizontal component of the vector field as the shadow cast on a right triangle.
How to calculate work done by a vector field on an object moving along a curve, by summing up infinitesimal forces.
Three common notations for line integrals of vector fields and their equivalence.
Parameterization of a curve as a prerequisite for calculating line integrals.
Simplification of line integral notation using the magnitude of the derivative of the parameterized curve.
Example problem: Evaluating the line integral of a vector field over a parabola from (0,0) to (2,8).
Step-by-step parameterization of the curve y=2x^2 and setting up the integral bounds.
Calculating the line integral using the differential form MDX + NDY and integrating from 0 to 2.
Integration result of the example problem, yielding a line integral value of 16.
Another example in 3D space, evaluating the line integral of a vector field over a parameterized curve.
Parameterization of the 3D curve and the setup for the line integral using M, N, and P components.
Integration of the 3D line integral, resulting in a value of 64.
Upcoming videos will cover more on circulation and flux with line integrals in vector fields.
Closing remarks, summarizing the video content and encouraging viewers to watch the next video.
Transcripts
Browse More Related Video

Conservative Fields & Path Independence (Vector Fields)

How to Calculate Flux (Line Integrals)

Conservative Vector Fields & Potential Functions

Lec 20: Path independence and conservative fields | MIT 18.02 Multivariable Calculus, Fall 2007
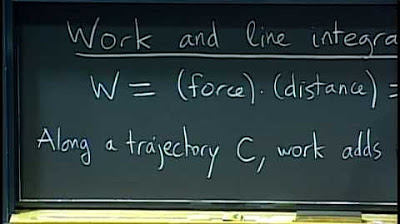
Lec 19: Vector fields and line integrals in the plane | MIT 18.02 Multivariable Calculus, Fall 2007

Example of closed line integral of conservative field | Multivariable Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: