Calculus 3: Green's Theorem (Video #30) | Math with Professor V

Math with Professor V

15 Jul 202041:26

EducationalLearning

32 Likes 10 Comments

TLDRThis calculus lecture introduces Green's Theorem, a fundamental concept for evaluating line integrals around simple closed curves and calculating the area of enclosed regions. The video explains the theorem's application in converting line integrals into double integrals, demonstrating through examples including non-conservative vector fields and regions with holes. It also showcases three methods to find areas using line integrals, illustrating the process with ellipses and other shapes, emphasizing the theorem's utility in various calculus problems.

Takeaways

📚 Green's Theorem allows the evaluation of a line integral around a simple closed curve by converting it into a double integral over the enclosed region.
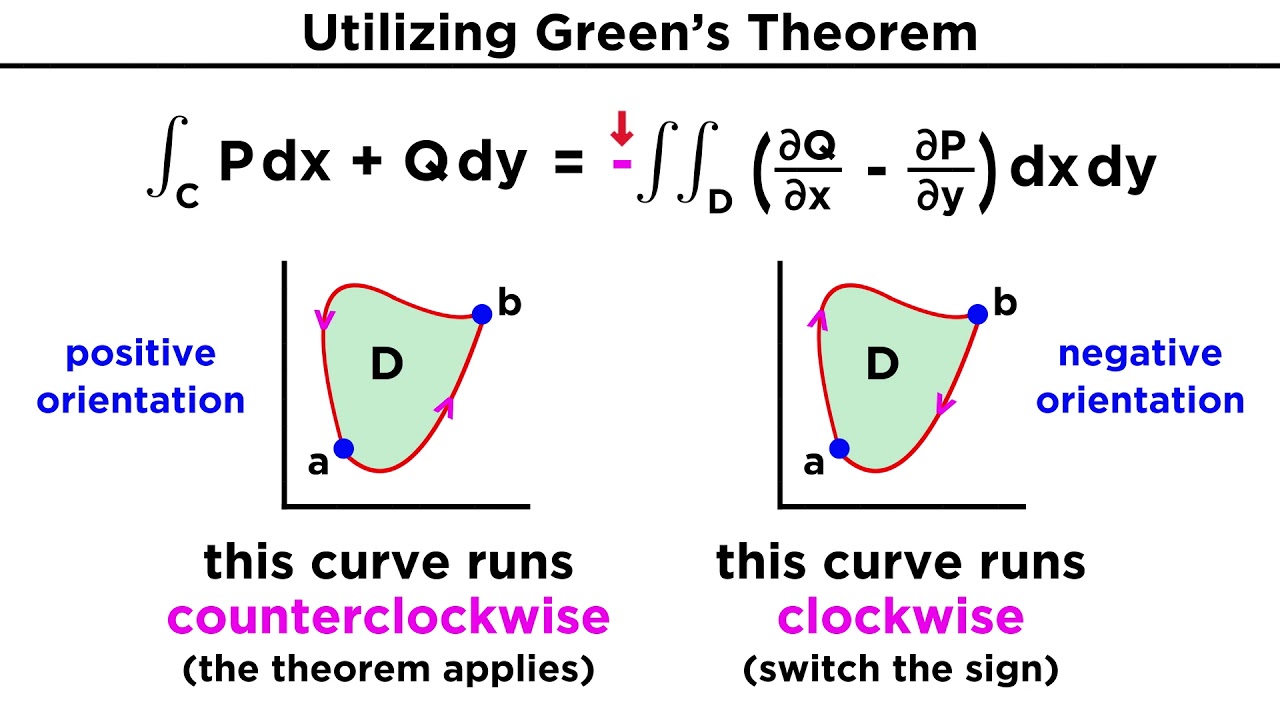
🔄 Positive orientation of a closed curve refers to a counterclockwise traversal, keeping the enclosed region on the left-hand side.
📐 The notation for a line integral around a positively oriented closed curve can be represented in multiple ways, including using the integral sign with the curve notation or the del operator with the boundary of the region.
🔍 The fundamental theorem for line integrals states that for a conservative vector field, the work done over any closed curve is zero, but this requires the vector field to meet specific conditions, such as equal mixed partials.
📝 The process of evaluating a line integral involves parametrizing the curve, finding derivatives dx and dy, and then integrating the given function components over the curve's parameter.
📉 Green's Theorem provides an alternative method to evaluate a line integral by using the double integral of the region enclosed by the curve, which can be more straightforward than direct line integral computation.
📏 The theorem can be applied to find the area of a region by setting up the double integral such that the integrand equals one, which corresponds to the area enclosed by the boundary curve.
🔄 Green's Theorem can be extended to regions with holes by subtracting the work done on the missing regions, effectively accounting for non-simply connected domains.
📈 The area of an ellipse can be found using a line integral approach, demonstrating the theorem's versatility in calculating areas of complex shapes.
📝 Three methods are presented for using line integrals to find areas: integrating x dy, integrating -y dx, and integrating (x dy - y dx)/2, each applicable depending on the specific problem setup.

Q & A

What is Green's Theorem and what does it allow us to evaluate?
-Green's Theorem is a result in vector calculus that allows us to evaluate a line integral around a simple closed curve by transforming it into a double integral over the region enclosed by that curve. It also provides a method to find the area of a region by calculating the line integral around it.
What is the definition of positive orientation of a simple closed curve?
-The positive orientation of a simple closed curve refers to a single counterclockwise traversal of the curve, ensuring that the enclosed region is always on the left side when walking along the curve.
How can the integral around a positively oriented closed curve be represented?
-The integral around a positively oriented closed curve can be represented as ∮(P dx + Q dy) along the curve C, where P and Q are the components of a vector field and C is the curve.
What is the significance of the fundamental theorem for line integrals in the context of Green's Theorem?
-The fundamental theorem for line integrals states that if a vector field is conservative, the work done on any closed curve is zero. This is significant because it simplifies the calculation of line integrals when the field is conservative, but Green's Theorem is needed for non-conservative fields.
How can you check if a vector field is conservative?
-A vector field is conservative if its mixed partial derivatives are equal, i.e., ∂P/∂y = ∂Q/∂x. If these conditions are not met, the field is not conservative.
What does Green's Theorem state for the evaluation of a line integral over a closed curve?
-Green's Theorem states that if a curve C is positively oriented and encloses a region D with continuous first partials for P and Q, then the line integral of P dx + Q dy over C is equal to the double integral of (∂Q/∂x - ∂P/∂y) dA over D.
How can Green's Theorem be used to find the area of a region enclosed by a curve?
-Green's Theorem can be used to find the area of a region by setting the integrand of the double integral to 1, which simplifies the line integral to the perimeter of the boundary curve times the enclosed area.
What is the difference between a simply connected region and a region with holes?
-A simply connected region is one where you cannot draw a simple closed curve within it that encloses any points outside the region. A region with holes is not simply connected because it contains one or more disjoint regions that are enclosed by simple closed curves.
How can you use Green's Theorem to evaluate the line integral over a curve that is not simply connected?
-For non-simply connected regions, you can use Green's Theorem by considering the line integral over the outer boundary with positive orientation and subtracting the line integral over the inner boundaries with negative orientation.
What are the three methods provided in the script to calculate the area of a region using a line integral?
-The three methods are: 1) Integrating over the closed curve C of x dy, 2) Integrating over the closed curve C of -y dx, and 3) Taking half the sum of both x dy and -y dx over the closed curve C.

Outlines

00:00

📚 Introduction to Green's Theorem

The lecture begins with an introduction to Green's Theorem, which is a fundamental concept in calculus that allows for the evaluation of a line integral around a simple closed curve by converting it into a double integral over the enclosed region. The theorem also provides a method for calculating the area of a region through a line integral. The concept of positive orientation for a closed curve is defined, emphasizing the counterclockwise traversal and the region being on the left-hand side. Notation for integrals around a closed curve is introduced, with examples of how to represent them using different symbols. The lecture then transitions into an example involving a non-conservative vector field, where the line integral is computed directly due to the lack of a potential function.

05:03

📐 Parametrization and Line Integrals

This section delves into the process of parametrizing a curve for the computation of a line integral. The example given involves a vector field with components that require the curve to be split into two pieces for parametrization, with special attention to maintaining the positive orientation. The lecture explains how to find the derivatives dx and dy for each curve segment and sets up the integrals with appropriate limits. The process of anti-differentiating to find the work done by the vector field is demonstrated, leading to the final calculation of the line integral.

10:03

🌀 Green's Theorem Application and Proof

The application of Green's Theorem to evaluate line integrals is explored, with the theorem stated formally. The theorem connects the line integral of a function around a closed curve to the double integral over the enclosed region, provided the function's first partial derivatives are continuous. A specific example is worked through, demonstrating how Green's Theorem simplifies the computation of a line integral by converting it into a double integral. The lecture also touches on the proof of Green's Theorem, discussing the assumptions and the approach to proving it for special cases, with an emphasis on the relationship between the line integral and the double integral.

15:10

🔍 Special Case Proof of Green's Theorem

The lecture continues with a detailed look at a special case for proving Green's Theorem. It involves assumptions about the region being both type one and type two, which allows for bounding in either the x or y direction. The process involves setting up integrals for the line integral around the region and the double integral over the region, then simplifying and showing their equivalence. The explanation includes the transformation of the double integral into an expression that matches the line integral, thus proving the theorem for this special case.

20:10

🛠 Using Green's Theorem for Work and Area

This part of the lecture illustrates how Green's Theorem can be used to calculate work represented by a line integral and to find the area of a region. An example of a line integral over a circle with a clockwise orientation is provided, showing how the theorem simplifies the calculation of work. The theorem is also extended to regions that are not simply connected, such as those with holes, by using additional line integrals with negative orientation to account for the missing regions.

25:14

🔄 Evaluating Line Integrals for Complex Regions

The lecture addresses the evaluation of line integrals for regions bounded by multiple circles, including those with holes. The process involves setting up the double integral using Green's Theorem and choosing the appropriate parametrization for the region, such as using polar coordinates for circular boundaries. The calculation is demonstrated for a region between two circles, showing how to account for the hole by adjusting the limits of integration.

30:15

📐 Finding Area Using Line Integrals

This section introduces methods to find the area of a region using line integrals, providing three different options based on Green's Theorem. The options involve setting up the integrand in specific ways to simplify the calculation of the area. The lecture then applies these methods to find the area of an ellipse using a parametric representation of its boundary, demonstrating how the area can be derived from the line integral of the ellipse's perimeter.

35:16

📘 Area Calculation for a Specific Region

The final part of the lecture focuses on calculating the area bounded by two lines using line integrals. The intersection points of the lines are determined, and the region to be bounded is graphed. The lecture then sets up the parametric representations for the line segments that form the boundary of the region and calculates the area using the chosen method from the previous section. The calculation involves integrating over the parametrized curves and simplifying the result to find the area.

40:20

📚 Conclusion on Green's Theorem

The lecture concludes with a summary of Green's Theorem, highlighting its utility in calculating work and area using line integrals. The various methods and examples covered throughout the lecture are briefly reviewed, emphasizing the theorem's significance and applications in calculus.

Mindmap

Keywords

💡Green's Theorem

Green's Theorem is a fundamental result in vector calculus that provides a way to convert a line integral around a simple closed curve into a double integral over the region enclosed by that curve. In the video, it is used to evaluate line integrals and find the area of a region. The theorem is central to the video's theme, as it is the main tool discussed and applied to various examples.

💡Line Integral

A line integral is an integral where the function to be integrated is evaluated along a curve. In the context of the video, line integrals are used to calculate work done by a vector field and to find areas of regions enclosed by curves. The script provides examples of how to compute line integrals directly and how Green's Theorem simplifies this process.

💡Double Integral

A double integral is an integral that extends over a two-dimensional region and is used to calculate quantities such as volume or area. In the video, double integrals are used in conjunction with Green's Theorem to find the area of a region by integrating over the region rather than along its boundary.

💡Conservative Vector Field

A conservative vector field is one where the work done by the field around any closed path is zero. This is because the field has a potential function whose gradient is the field itself. In the script, the concept is used to explain when Green's Theorem can simplify to zero work for closed curves in conservative fields.

💡Positive Orientation

Positive orientation refers to the counterclockwise traversal of a curve, which is the standard direction assumed in the video when discussing line integrals and applying Green's Theorem. The concept is crucial for correctly setting up integrals and ensuring that the enclosed region is on the left-hand side as one traverses the curve.

💡Parametric Representation

Parametric representation is a method of describing a curve by expressing its coordinates as functions of a parameter. In the video, parametric representations are used to define curves for which line integrals are computed, especially when the curves are parts of more complex shapes.

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system where points are defined by a radius from a central point and an angle from a reference direction. The video script uses polar coordinates to simplify the computation of double integrals in regions bounded by circles, taking advantage of the symmetry in these shapes.

💡Ellipse

An ellipse is a geometric shape defined by the sum of the squares of the distances from any point on the shape to two fixed points, called foci, being constant. In the script, an example is given where Green's Theorem is used to find the area of an ellipse using a line integral, illustrating the theorem's application to non-circular shapes.

💡Area Calculation

Area calculation is the process of determining the size of a two-dimensional region. The video demonstrates how Green's Theorem can be used to calculate areas of regions enclosed by curves by transforming the problem into a line integral or a double integral.

💡Flux

Flux is a concept related to the flow of a quantity across a surface, often used in physics to describe the movement of a field through a boundary. Although not explicitly defined in the script, the term is alluded to in the context of discussing line integrals and their applications, which can be related to flux in certain physical interpretations.

Highlights

Green's Theorem allows the evaluation of line integrals around a simple closed curve by converting them into double integrals over the enclosed region.

The theorem provides a method to find the area of a region by calculating the line integral around it.

Positive orientation of a curve refers to a counterclockwise traversal, keeping the enclosed region on the left-hand side.

Line integral notation can vary but represents the same concept, integral around a positively oriented closed curve.

Fundamental Theorem of Line Integrals states that work on any closed curve in a conservative vector field is zero.

Non-conservative vector fields require direct computation of line integrals without a potential function.

Parametrization of curves is necessary for computing line integrals, demonstrated with a line segment and a circular arc.

Green's Theorem is applicable for evaluating work represented by line integrals when the vector field is non-conservative.

Double integrals can be used to find the area of a region using Green's Theorem, avoiding the need for parametric representation.

Green's Theorem can be extended to regions with holes by subtracting the work around the missing regions.

The area of a region can be found using line integrals by setting the integrand equal to one, representing several methods.

Parametrization of an ellipse leads to the derivation of its area using line integrals and Green's Theorem.

The area of a region bounded by linear equations can be found using line integrals and appropriate parametrization.

Green's Theorem simplifies the process of finding areas and work by converting complex line integrals into manageable double integrals.

The theorem's practical applications include calculating work and areas in various geometric contexts.

A partial proof of Green's Theorem is provided for a special case, demonstrating the relationship between line and double integrals.

Transcripts

Browse More Related Video

Lec 22: Green's theorem | MIT 18.02 Multivariable Calculus, Fall 2007

Lec 24: Simply connected regions; review | MIT 18.02 Multivariable Calculus, Fall 2007

Lec 20: Path independence and conservative fields | MIT 18.02 Multivariable Calculus, Fall 2007

Green's Theorem

Lec 21 | MIT 18.01 Single Variable Calculus, Fall 2007

Conservative Fields & Path Independence (Vector Fields)

Related Tags

Green's Theorem Calculus Line Integrals Double Integrals Vector Fields Conservative Fields Area Calculation Parametric Curves Polar Coordinates Ellipse Area