Dot Products (In 3-dimensional Space)

Houston Math Prep
24 Jan 202111:39
EducationalLearning
32 Likes 10 Comments

TLDRThis video script from Houston Math Prep explains the concept of dot products in 2D and 3D vector spaces, demonstrating the calculation process through examples. It highlights the difference between dot products and other vector operations, as they result in a scalar rather than a vector. The script also delves into the geometric interpretation of dot products, showing how they relate to the angle between vectors and the magnitudes of those vectors. It includes practical examples of finding the angle between vectors using the dot product and discusses the implications of positive, negative, and zero dot products for acute, obtuse, and orthogonal angles, respectively.

Takeaways
  • 📚 The script introduces the concept of dot products in 2D and 3D space, explaining the process of calculating them by multiplying corresponding components and summing the results.
  • 🔢 The dot product results in a scalar, not a vector, which is a key difference from other vector operations like addition or scalar multiplication.
  • 📈 The script provides examples of calculating dot products with vectors in 3D space, demonstrating the step-by-step process with specific vectors.
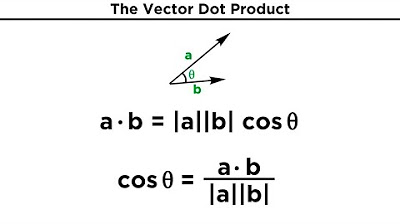
  • 📉 The dot product is used to determine the relationship between the lengths of vectors and the angle between them, as shown by the formula involving the dot product, magnitudes, and the cosine of the angle.
  • 📐 The script explains how to rearrange the dot product formula to solve for the cosine of the angle between two vectors, which is useful for finding the angle itself.
  • 🔍 An example is given to show how to calculate the angle between two vectors using the dot product and magnitudes, including the use of inverse cosine.
  • 🔑 The script mentions that the sign of the dot product can quickly indicate whether the angle between vectors is acute (positive dot product), obtuse (negative dot product), or right angles (dot product equals zero).
  • 📝 The process of determining when two vectors are orthogonal by setting their dot product to zero is explained, with an example showing how to find a specific value that makes the vectors orthogonal.
  • 📚 The script emphasizes the convenience of the dot product for quickly estimating the angle between vectors without fully calculating the angle.
  • 📉 The law of cosines is mentioned as the origin of the dot product formula, though the proof is not shown in the script.
  • 👍 The video concludes with a summary of the importance of understanding dot products for analyzing the relationship between vectors.
Q & A

  • What is a dot product and how is it calculated?

    -A dot product is a mathematical operation that takes two vectors and returns a scalar. It is calculated by multiplying corresponding components of the two vectors and then summing those products. For example, for vectors v and w in 2D space, the dot product is v1*w1 + v2*w2. In 3D space, it involves an additional component: v1*w1 + v2*w2 + v3*w3.

  • What is the difference between vector addition and dot product in terms of the result type?

    -Vector addition results in a vector, as does scalar multiplication. However, the dot product of two vectors results in a scalar, which is a real number, not a vector.

  • Can you provide an example of calculating the dot product of two 3D vectors?

    -Sure. If vector v is (3, 5, -1) and vector w is (-2, 1, -4), the dot product v·w is calculated as (3*-2) + (5*1) + (-1*-4) = -6 + 5 + 4, which equals 3.

  • How can the dot product be used to find the angle between two vectors?

    -The dot product can be related to the angle between two vectors by the formula: v·w = ||v|| * ||w|| * cos(θ), where ||v|| and ||w|| are the magnitudes of vectors v and w, and θ is the angle between them. By rearranging this formula, you can solve for cos(θ) and then find the angle using the inverse cosine function.

  • What is the significance of the sign of the dot product in determining the angle between two vectors?

    -A positive dot product indicates an acute angle (less than 90 degrees) between the vectors, as cosine is positive in quadrant 1. A negative dot product indicates an obtuse angle (greater than 90 degrees), as cosine is negative in quadrant 2. A dot product of zero indicates that the vectors are orthogonal (perpendicular) to each other.

  • How can you determine if two vectors are orthogonal using the dot product?

    -Two vectors are orthogonal if the angle between them is exactly 90 degrees. This is the case when the dot product of the vectors is zero. If v·w = 0, the vectors are orthogonal.

  • Can you give an example of finding the value of 'a' that makes two vectors orthogonal?

    -If we have vectors v = (3a, 4, -1) and w = (a, -2, 6), and we want them to be orthogonal, we set their dot product to zero: 3a*a + 4*(-2) + (-1)*6 = 0. Solving this gives a = 14/3.

  • What is the magnitude of a vector and how is it calculated?

    -The magnitude of a vector is its length and is calculated as the square root of the sum of the squares of its components. For a 3D vector (x, y, z), the magnitude is √(x^2 + y^2 + z^2).

  • Why is the dot product useful for getting a quick idea of the angle between vectors?

    -The dot product provides a scalar value that is directly related to the cosine of the angle between two vectors. It is computationally efficient and can quickly indicate whether the angle is acute, obtuse, or if the vectors are orthogonal, without needing to calculate the exact angle.

  • What is the relationship between the dot product and the law of cosines?

    -The formula for the dot product of two vectors is derived from the law of cosines. The dot product v·w equals the product of the magnitudes of the vectors and the cosine of the angle between them, which is a direct application of the law of cosines in vector form.

  • Can the dot product be used to determine the direction of vectors?

    -While the dot product itself does not directly indicate direction, the sign of the dot product (positive, negative, or zero) can provide information about the relative orientation of two vectors with respect to each other, such as whether the angle between them is acute, obtuse, or 90 degrees.

Outlines
00:00
📚 Introduction to Dot Products in Vectors

The script introduces the concept of dot products in 2D and 3D vectors, explaining the process of calculating them by multiplying corresponding components and then summing the results. It emphasizes the difference between the dot product and other vector operations, noting that the dot product results in a scalar rather than a vector. Examples are provided to demonstrate the calculation of the dot product for given vectors in 3D space, illustrating the process with step-by-step multiplication and addition of components.

05:00
🔍 Understanding the Dot Product's Significance

This paragraph delves into the significance of the dot product, explaining its relationship with the magnitudes of vectors and the angle between them. It presents the formula that relates the dot product to the product of the vectors' magnitudes and the cosine of the angle (theta) between them, derived from the law of cosines. The script rearranges the formula to solve for the cosine of theta, facilitating the calculation of the angle between two vectors. An example calculation is provided, demonstrating how to find the angle between two given vectors using their dot product and magnitudes, ultimately using the inverse cosine function to determine the angle in degrees.

10:00
📐 Applications and Properties of Dot Products

The final paragraph discusses the practical applications and properties of dot products, particularly in determining the angle between vectors. It explains how the sign of the dot product can indicate whether the angle between vectors is acute (less than 90 degrees), obtuse (greater than 90 degrees), or right (exactly 90 degrees, indicating orthogonality). The script provides a method to check for orthogonality by setting the dot product to zero and solving for the specific component that makes the vectors perpendicular. An example problem is presented, where the value of 'a' is determined to make two vectors orthogonal, reinforcing the concept with a practical application.

Mindmap
Keywords
💡Dot Product
The dot product, also known as the scalar product, is a binary operation that takes two vectors and returns a single number. In the context of the video, it is calculated by multiplying corresponding components of two vectors and summing those products. The dot product is central to the video's theme as it is used to determine the relationship between the lengths of vectors and the angle between them. For example, the script explains how to calculate the dot product of vectors v and w in both 2D and 3D spaces.
💡Component-wise Multiplication
Component-wise multiplication is the process of multiplying corresponding elements of two vectors. It is a fundamental step in calculating the dot product, as demonstrated in the video script where the first component of vector v is multiplied by the first component of vector w, and so on for each pair of corresponding components.
💡Scalar
A scalar is a single numerical value, as opposed to a vector, which has both magnitude and direction. In the video, it is mentioned that the result of a dot product is a scalar, not a vector. This distinction is important because it highlights the different nature of the dot product compared to other vector operations such as vector addition or scalar multiplication.
💡Magnitude
The magnitude of a vector is its length, calculated as the square root of the sum of the squares of its components. In the script, the magnitude is used in the formula for the dot product in relation to the angle between two vectors, showing how the dot product can be related to the geometric properties of the vectors.
💡Angle Between Vectors
The angle between vectors is the measure of the space between two vectors originating from the same point. The video script discusses how the dot product can be used to find this angle using the formula that relates the dot product to the magnitudes of the vectors and the cosine of the angle between them.
💡Cosine of Theta
Cosine of Theta (where Theta is the angle between two vectors) is used in the formula to relate the dot product to the geometric relationship between vectors. The script explains how the dot product formula can be rearranged to solve for the cosine of the angle, which is useful for finding the angle between two vectors.
💡Law of Cosines
The Law of Cosines is a formula used in geometry to relate the lengths of the sides of a triangle to the cosine of one of its angles. In the video script, it is mentioned that the formula for the dot product in terms of the angle between vectors comes from the Law of Cosines, although the proof is not shown.
💡Orthogonal Vectors
Orthogonal vectors are vectors that are perpendicular to each other, forming an angle of 90 degrees. The script explains that if the dot product of two vectors is zero, the vectors are orthogonal. This concept is demonstrated with an example where the value of 'a' is determined to make two vectors orthogonal.
💡Acute Angle
An acute angle is an angle less than 90 degrees. The script mentions that if the angle between two vectors is acute, the cosine of that angle is positive, and therefore, the dot product of the vectors will also be positive.
💡Obtuse Angle
An obtuse angle is an angle greater than 90 degrees but less than 180 degrees. The video script explains that if the angle between two vectors is obtuse, the cosine of that angle is negative, indicating that the dot product of the vectors will be negative.
💡Inverse Cosine
The inverse cosine, often represented as arccos or cos^-1, is the inverse function of the cosine. In the script, it is used to find the angle between two vectors by taking the inverse cosine of the ratio of the dot product to the product of the magnitudes of the vectors.
Highlights

Introduction to dot products in 2D and 3D space, explaining the component-wise multiplication and addition process.

Dot products result in a scalar, unlike vector addition or scalar multiplication which result in vectors.

Example calculation of the dot product for 3D vectors v and w, resulting in a positive 3.

Second example of dot product calculation for different 3D vectors, resulting in negative 9.

Explanation of the dot product's relationship with the magnitudes of vectors and the angle between them.

Presentation of the formula relating dot product to vector magnitudes and the cosine of the angle between them.

Demonstration of how to rearrange the formula to solve for the cosine of the angle between two vectors.

Example of finding the angle between two vectors using the dot product formula, yielding approximately 74.19 degrees.

Discussion on using the sign of the dot product to determine if the angle between vectors is acute, obtuse, or right angle.

Quick method to check if vectors are orthogonal by verifying if their dot product equals zero.

Application problem solving for finding the value of 'a' that makes two vectors orthogonal.

Explanation of how the sign of the dot product indicates the quadrant of the angle between vectors.

Clarification that a positive dot product indicates an acute angle, while a negative one suggests an obtuse angle.

The convenience of the dot product for quickly estimating the angle between vectors without full calculation.

Summary of the practical applications and theoretical understanding gained from the discussion on dot products.

Transcripts

Browse More Related Video

The Vector Dot Product

Angle between vectors leads to defining the Dot Product | Multivariable Calculus

Cross Product and Dot Product: Visual explanation

The Box Product (Triple Scalar Product)

Dot products and duality | Chapter 9, Essence of linear algebra

Vector Projections and Scalar Projections (Calculus 3)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Dot ProductVector Math2D Space3D SpaceMath TutorialAngle CalculationComponent-wiseEducational ContentHouston MathVector OrthogonalityCosine Law