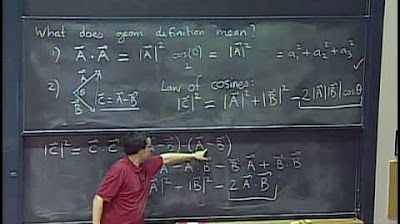Dot products and duality | Chapter 9, Essence of linear algebra

3Blue1Brown

24 Aug 201614:11

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the concept of dot products in linear algebra, emphasizing their geometric interpretation as projections and their deeper connection to linear transformations. It explains how dot products can be seen as a transformation from vectors to numbers, highlighting the duality between vectors and transformations. The script uses the example of projecting 2D vectors onto a diagonal number line to illustrate how the dot product with a unit vector represents the length of the projection, and how this extends to non-unit vectors by scaling the projection length. This exploration reveals the beauty of mathematical duality, where vectors and transformations are intricately linked.

Takeaways

🎵 The 'Ode to Joy' by Beethoven is used as a backdrop to discuss linear algebra concepts.
🔢 Dot products are typically introduced early in a linear algebra course and involve multiplying corresponding components of two vectors and summing the results.
📐 A deeper understanding of dot products is linked to linear transformations, which are not fully explored until later in a course.
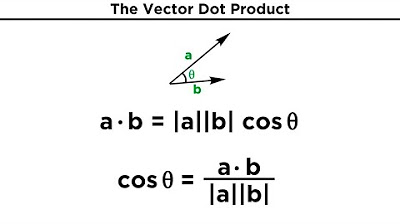
🌟 The geometric interpretation of a dot product involves projecting one vector onto the line defined by the origin and the other vector, with the product of the projection's length and the other vector's length giving the dot product.
🔄 The dot product is commutative, meaning the order of the vectors does not affect the result.
📈 Scaling a vector affects the dot product by multiplying the result by the scale factor, regardless of the interpretation used (projecting the scaled vector or the original onto the other).
🤔 The numerical process of computing a dot product is related to the concept of projection, which may not be immediately apparent.
🔄 Linear transformations that map vectors to numbers, particularly those that preserve the even spacing of points, are restricted in a way that only certain functions can be considered linear.
📏 A 1x2 matrix can represent a linear transformation from multiple dimensions to one, and this is computationally similar to a dot product with a 2D vector.
🌐 The concept of duality in mathematics refers to a natural but surprising correspondence between two types of mathematical entities, such as vectors and transformations.
🎭 The dot product is not just a geometric tool; it also serves as a bridge between vectors and the world of linear transformations, allowing for a deeper understanding of vectors as embodiments of transformations.

Q & A

Why does the presenter delay introducing dot products in the series?
-The presenter delays introducing dot products to provide a fuller understanding under the context of linear transformations, which offers more insight than the standard introduction that requires only a basic understanding of vectors.
What is the standard numerical procedure to compute the dot product of two vectors?
-The standard numerical procedure involves pairing up corresponding coordinates of two vectors of the same dimension, multiplying each pair together, and then adding up all the results to get the dot product.
How is the geometric interpretation of the dot product described?
-The geometric interpretation of the dot product involves projecting one vector onto the line passing through the origin and the tip of another vector, and then multiplying the length of this projection by the length of the other vector to get the dot product.
What does the sign of the dot product indicate about the direction of the two vectors involved?
-The sign of the dot product indicates the general direction of the two vectors: if positive, they are generally pointing in the same direction; if zero, they are perpendicular; and if negative, they point in generally opposite directions.
Why does the order of vectors in a dot product not affect the result?
-The order of vectors in a dot product does not affect the result due to the symmetry involved. If the vectors have the same length, projecting one onto the other and multiplying by the length is a mirror image of doing the reverse, and scaling one vector maintains this equivalence.
How does scaling one of the vectors affect the dot product?
-Scaling one of the vectors by a constant factor scales the dot product by the same factor. This holds true regardless of whether you consider the projection of one vector onto the other or vice versa, due to the linear properties of the dot product.
What is the connection between dot products and linear transformations from multiple dimensions to one dimension?
-Dot products are closely related to linear transformations that take a vector from a higher dimension to a single number on the number line. These transformations are linear and their effect on vectors can be represented by the computation of a dot product.
How can a 1x2 matrix be associated with a 2D vector in the context of linear transformations?
-A 1x2 matrix, which represents a linear transformation from 2D vectors to numbers, can be associated with a 2D vector by tilting the numerical representation of the vector on its side to form the matrix, and vice versa.
What role does the vector u-hat play in the geometric interpretation of dot products and linear transformations?
-The vector u-hat, situated such that it overlaps with the diagonal number line, plays a crucial role in defining a linear transformation from 2D vectors to numbers through projection. The coordinates of u-hat determine the transformation matrix, which in turn relates to the dot product.
What is the significance of duality in the context of the dot product and linear transformations?
-Duality, in this context, refers to the natural correspondence between vectors and linear transformations. Specifically, any linear transformation from a space to one dimension has a unique vector such that applying the transformation is equivalent to taking a dot product with that vector. This showcases the deep interconnection between geometric and algebraic perspectives in linear algebra.

Outlines

00:00

📚 Introduction to Dot Products and Linear Transformations

This paragraph introduces the concept of dot products, typically taught early in a linear algebra course, and explains the decision to discuss them later in the series to provide a deeper understanding through the context of linear transformations. The standard numerical definition of dot products is explained, where two vectors of the same dimension are paired, multiplied together, and summed. The geometric interpretation of dot products as projections is also discussed, highlighting how the dot product can be negative, zero, or positive depending on the direction of the vectors. The asymmetry in the interpretation is addressed, and the concept of duality is introduced as a key to understanding the full significance of dot products in relation to linear transformations.

05:04

📐 Geometric Interpretation and Linear Transformations

This paragraph delves deeper into the geometric interpretation of dot products, using the concept of projection to explain the numerical process. It introduces the idea of linear transformations from multiple dimensions to one, focusing on their visual properties and how they relate to evenly spaced dots in the output space. The example of a linear transformation is given, where the transformation of basis vectors is used to define a 1x2 matrix. The connection between this numerical operation and the dot product of two vectors is explored, highlighting the association between 1x2 matrices and 2D vectors. The significance of this relationship from a geometric viewpoint is emphasized, showing how linear transformations to numbers and vectors are intrinsically linked.

10:04

🌟 The Duality of Vectors and Transformations

The final paragraph discusses the concept of duality in mathematics, particularly in the context of linear algebra. It explains how a linear transformation from 2D space to the number line, defined by projection, is necessarily described by a 1x2 matrix, and how this is computationally identical to taking a dot product with a certain vector. The paragraph clarifies the interpretation of dot products with non-unit vectors as a projection followed by a scaling of the projection's length. The beauty of this duality is highlighted, where a vector can be seen as the conceptual embodiment of a linear transformation, simplifying the understanding of mathematical concepts. The paragraph concludes by setting the stage for further exploration of this duality in the context of the cross product in future discussions.

Mindmap

Keywords

💡Dot Product

The dot product is a fundamental operation in linear algebra, defined as the sum of the products of corresponding entries of two sequences of numbers (vectors). This concept is pivotal in understanding geometrical and algebraic properties of vectors in spaces. In the video, it's illustrated with examples like the dot product of vectors (1, 2) and (3, 4), emphasizing its numerical computation and its deeper geometric interpretation related to the projection of vectors onto one another. This leads to insights about the directionality and magnitude of vectors, demonstrating its significance beyond simple arithmetic.

💡Linear Transformations

Linear transformations are functions between vector spaces that preserve vector addition and scalar multiplication. The video delves into how understanding dot products is enriched by the concept of linear transformations, particularly emphasizing transformations from multiple dimensions to one dimension (the number line). This connection highlights how dot products relate to the core operations of linear algebra, tying them to the broader framework of transforming spaces and the manipulation of vectors within these spaces.

💡Geometric Interpretation

The geometric interpretation of the dot product relates to projecting one vector onto another and examining the relationship of their lengths and directions. The video emphasizes this interpretation by showing how the dot product reveals whether vectors point in the same direction (positive dot product), are perpendicular (zero dot product), or point in opposite directions (negative dot product). This geometric perspective is crucial for visualizing and understanding the interaction between vectors in space.

💡Vector Projection

Vector projection is the process of projecting one vector onto another vector or a line, which is central to understanding the dot product's geometric meaning. The video uses this concept to explain how the dot product quantifies the extent to which two vectors align with each other directionally and in magnitude, by considering the projection of one vector onto another and multiplying it by the vector's length.

💡Symmetry and Scaling

Symmetry and scaling in the context of dot products refer to the properties that the dot product remains unchanged under the interchange of the two vectors involved and scales linearly with the vectors. The video explores these ideas by discussing how scaling a vector affects the dot product, illustrating the underlying symmetry that makes the dot product commutative and how scaling one vector impacts the result in a predictable way.

💡Duality

Duality is a broad concept across mathematics, described in the video as the relationship between vectors and linear transformations. Specifically, it's shown that any linear transformation can be associated with a unique vector such that applying the transformation is equivalent to taking a dot product with that vector. This concept is pivotal in the script for linking the geometric interpretation of the dot product with the algebraic operations of linear transformations, showcasing the deep interconnectedness of these concepts.

💡Linear Transformation to One Dimension

The video discusses linear transformations that map vectors from a higher-dimensional space to a one-dimensional space (the number line). This specific type of transformation is used to bridge the concept of the dot product with that of linear transformations, illustrating how projecting a vector onto another and measuring its magnitude on the number line encapsulates both a geometric operation and an instance of a linear transformation.

💡Matrix Representation

Matrix representation in the context of the video refers to expressing linear transformations as matrices, which is a fundamental concept in linear algebra for describing and computing transformations. The video specifically mentions 1x2 matrices as representations of linear transformations from 2D to 1D, paralleling these with the process of taking a dot product, thus highlighting the algebraic structure underlying geometric interpretations.

💡Unit Vectors

Unit vectors are vectors with a magnitude of one, serving as the basic building blocks for vector spaces. The video uses unit vectors to explain how dot products can represent projections and lengths when vectors are projected onto the span of these unit vectors, illustrating the practical significance of unit vectors in simplifying the understanding of vector interactions and transformations.

💡Vector Spaces

Vector spaces are collections of vectors that can be added together and multiplied (scaled) by numbers, called scalars. The script refers to vector spaces when discussing linear transformations and the projection of vectors onto lines or planes within these spaces. This concept underpins the video's exploration of linear algebra, providing the foundational framework within which vectors are manipulated and understood.

Highlights

Introduction of dot products in the context of linear transformations.

Standard numerical definition of dot products involving coordinate multiplication and summation.

Geometric interpretation of dot products as projections and lengths.

Explanation of why the order of vectors in a dot product does not matter.

Discussion on the asymmetry in the geometric interpretation of dot products.

Intuition on the effect of scaling a vector and its impact on dot products.

Connection between numerical processes and geometric projections in the context of dot products.

Introduction to linear transformations from multiple dimensions to one dimension.

Visual property of linear transformations keeping evenly spaced points on the output space.

Example of a linear transformation applied to a vector and its numerical representation.

Association between 1x2 matrices and 2D vectors through matrix-vector multiplication.

Clarification of the relationship between linear transformations and vectors through projection.

Demonstration of a linear transformation from 2D vectors to numbers through projection onto a number line.

Derivation of the 1x2 matrix describing the projection transformation from the coordinates of a unit vector.

Interpretation of the dot product with a non-unit vector as a scaled projection.

Explanation of duality in mathematics and its manifestation in the relationship between vectors and linear transformations.

Insight that vectors can be conceptualized as the embodiment of linear transformations.

Anticipation of further exploration of duality in the context of the cross product in future content.

Transcripts

Browse More Related Video

Dot Products (In 3-dimensional Space)

Lec 1: Dot product | MIT 18.02 Multivariable Calculus, Fall 2007

The Vector Dot Product

Vector Projections and Scalar Projections (Calculus 3)

Angle between vectors leads to defining the Dot Product | Multivariable Calculus

Jacobian prerequisite knowledge

Dot products and duality | Chapter 9, Essence of linear algebra

Takeaways

Q & A

Why does the presenter delay introducing dot products in the series?

What is the standard numerical procedure to compute the dot product of two vectors?

How is the geometric interpretation of the dot product described?

What does the sign of the dot product indicate about the direction of the two vectors involved?

Why does the order of vectors in a dot product not affect the result?

How does scaling one of the vectors affect the dot product?

What is the connection between dot products and linear transformations from multiple dimensions to one dimension?

How can a 1x2 matrix be associated with a 2D vector in the context of linear transformations?

What role does the vector u-hat play in the geometric interpretation of dot products and linear transformations?

What is the significance of duality in the context of the dot product and linear transformations?