Angle between vectors leads to defining the Dot Product | Multivariable Calculus
TLDRThis educational video delves into the concept of the dot product and its geometric interpretation through the lens of the Doppler effect. It begins with a fundamental problem of finding the angle between two vectors, U and V, by forming a triangle with the vector U-V. The script introduces the cosine law to calculate the angle, leading to the definition of the dot product as the sum of the products of corresponding vector components. The video further explains how the dot product can determine orthogonality, where vectors are perpendicular with an angle of 90 degrees and a dot product of zero, highlighting its significance in vector mathematics.
Takeaways
- 📚 The video discusses a geometric problem involving finding the angle between two vectors, U and V, using the cosine law.
- 📐 The script introduces the concept of using the vector U - V to form a triangle with vectors U and V, allowing the application of geometric rules.
- 🔍 The cosine law is explained as a formula that relates the lengths of the sides of a triangle to the cosine of the included angle.
- 📈 The script explains how to calculate the lengths of vectors U and V squared, and the length of U - V squared, using their components.
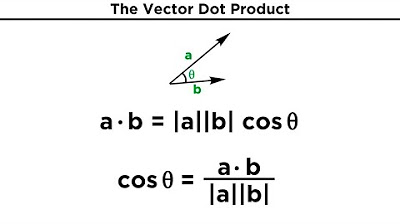
- 📝 The dot product is derived from the expansion of the cosine law formula, highlighting its importance in vector mathematics.
- 🧩 The dot product is defined as the sum of the products of the corresponding components of two vectors.
- 🔢 The script provides a formula to calculate the angle between two vectors using the dot product and the lengths of the vectors.
- 📉 The angle formula simplifies to arc cosine of the dot product divided by the product of the lengths of the vectors.
- 🦄 The video introduces a special case where the angle between two vectors is 90 degrees, leading to the dot product being zero.
- 🔄 The concept of orthogonal vectors is defined, where the dot product is zero, indicating a 90-degree angle between them.
- 📌 The script notes a discrepancy in the definition of orthogonality when one of the vectors can be the zero vector, which was not considered in the initial angle discussion.
Q & A
What operation on vectors is discussed in the video?
-The video discusses the operation on vectors known as the dot product, which is related to the angle between two vectors.
How can the angle between two vectors be found using geometry?
-The angle between two vectors can be found using the cosine law, which relates the lengths of the sides of a triangle formed by the two vectors and the vector resulting from their difference.
What is the significance of the vector u - v in the context of the video?
-The vector u - v represents the third side of the triangle formed by the vectors u and v, which is used in applying the cosine law to find the angle between them.
What is the formula for the length of a vector squared in three dimensions?
-The length of a vector squared in three dimensions is given by the sum of the squares of its components, i.e., \( u^2 = u_1^2 + u_2^2 + u_3^2 \) for vector u.
How is the length of the vector u - v squared calculated?
-The length of the vector u - v squared is calculated by summing the squares of the differences of the corresponding components of vectors u and v, i.e., \( (u - v)^2 = (u_1 - v_1)^2 + (u_2 - v_2)^2 + (u_3 - v_3)^2 \).
What is the dot product of two vectors, and how is it defined?
-The dot product of two vectors is a scalar value obtained by multiplying the corresponding components of the vectors and summing the results. It is defined as \( \text{u} \cdot \text{v} = u_1v_1 + u_2v_2 + u_3v_3 \) for three-dimensional vectors.
How is the dot product related to the angle between two vectors?
-The dot product is related to the angle between two vectors through the cosine of the angle, which is the dot product divided by the product of the magnitudes of the two vectors.
What is the formula for the angle between two vectors using the dot product?
-The formula for the angle between two vectors using the dot product is \( \theta = \arccos\left(\frac{\text{u} \cdot \text{v}}{\|\text{u}\|\|\text{v}\|}\right) \), where \( \theta \) is the angle, \( \text{u} \cdot \text{v} \) is the dot product, and \( \|\text{u}\|\|\text{v}\| \) is the product of the magnitudes of vectors u and v.
What does it mean for two vectors to be orthogonal?
-Two vectors are orthogonal if the angle between them is 90 degrees (or \( \pi/2 \) radians), which means their dot product is zero.
How does the video handle the special case where the angle between two vectors is 90 degrees?
-In the special case where the angle is 90 degrees, the dot product of the two vectors is zero, which leads to the definition of orthogonality, where the vectors are said to be perpendicular to each other.
What is the discrepancy mentioned in the video regarding the definition of orthogonal vectors?
-The discrepancy mentioned is that the definition of orthogonal vectors allows for the possibility of the vectors being zero, whereas the previous discussion of angles insisted on nonzero vectors.
Outlines
📚 Understanding Vector Angles and the Dot Product
This paragraph introduces the concept of finding the angle between two vectors, U and V, by forming a triangle with the third side as vector U minus V. The cosine law is applied to this triangle to derive an equation involving the dot product, which is defined as the sum of the products of corresponding vector components. The paragraph explains how the dot product can be used to calculate the angle between two vectors and introduces the concept of orthogonality, where the dot product equals zero, indicating a 90-degree angle between the vectors.
🔍 Special Case of Orthogonal Vectors
The second paragraph focuses on a special case where the angle between two vectors is 90 degrees (PI/2 radians). It demonstrates that when the dot product of two vectors is zero, the vectors are orthogonal to each other. The explanation includes taking the cosine of both sides of the equation derived from the cosine law, leading to the conclusion that the dot product is zero when the cosine of the angle is zero. This paragraph also notes the discrepancy in the definition of orthogonality when one of the vectors is zero, which was not considered in the initial explanation of the angle between vectors.
Mindmap
Keywords
💡Doppler
💡Dot Product
💡Vector
💡Angle
💡Cosine Law
💡Length of a Vector
💡Orthogonal
💡Scalar
💡Components
💡Geometry
Highlights
Introduction to the concept of the Doppler operation on vectors.
Starting with a geometric problem involving two vectors, U and V, and the angle between them.
Formation of a triangle by considering the third side as the vector U minus V.
Application of the cosine law to find the angle between two vectors.
Expression of the length of vectors U and V in terms of their components.
Expansion of the length of U minus V squared to find the relationship between vector components.
Derivation of the formula for the angle between vectors using the dot product.
Definition of the dot product for two vectors in terms of their components.
Explanation of the dot product as a scalar output from the multiplication of two vectors.
Special case example where the angle theta is 90 degrees (PI/2 radians).
Condition for vectors to be orthogonal: the dot product equals zero.
Clarification on the definition of orthogonal vectors, including the zero vector case.
The dot product as a key component in determining the angle between vectors.
Geometric interpretation of the dot product in the context of vector angles.
Practical application of the cosine law in vector operations.
Importance of the dot product in vector mathematics and its various uses.
Final summary of the angle formula between two vectors using the dot product.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: