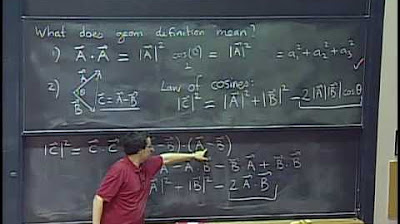Unit Vectors & Scalar Multiplication (in 3 dimensions)

Houston Math Prep

17 Jan 202114:13

EducationalLearning

32 Likes 10 Comments

TLDRThis video from Houston Math Prep delves into the concept of unit vectors in three-dimensional space (R3), starting with a refresher on scalar multiplication. It explains how scalar multiplication scales the length of a vector while maintaining its direction. The script then introduces unit vectors, which are vectors of magnitude one, and discusses standard unit vectors in R3, i, j, and k, along with their orthogonal properties. The video also covers how to express any vector as a linear combination of these unit vectors. Finally, it demonstrates how to find a unit vector in the direction of a given vector by dividing it by its magnitude, with examples provided.

Takeaways

📚 Scalar multiplication involves multiplying a vector by a real number, distributing the multiplication across each component of the vector.
🔍 Geometrically, scalar multiplication changes the magnitude (length) of the vector while keeping it parallel to the original vector.
📏 The magnitude of a vector in 3D space is calculated using the square root of the sum of the squares of its components.
🦠 Multiplying a vector by a scalar greater than one increases the vector's length, while a scalar less than one decreases it.
➡️ Scalar multiplication by negative one results in a vector with the same magnitude but pointing in the opposite direction.
🚫 Multiplying a vector by zero yields the zero vector, which has no specific direction and a magnitude of zero.
🎯 A unit vector is a vector with a magnitude of one, representing a direction without a specific length.
📌 Standard unit vectors in 3D space, denoted as î, ĵ, and k̂, point in the positive x, y, and z directions respectively.
🔄 Any vector can be expressed as a linear combination of standard unit vectors, indicating the direction and magnitude in each axis.
🌐 To find a unit vector in the direction of a given vector, divide the vector by its magnitude.
📘 The script provides examples of finding unit vectors for given vectors by dividing them by their respective magnitudes, resulting in vectors of unit length pointing in the same direction.

Q & A

What is scalar multiplication in the context of 3D space?
-Scalar multiplication is the process of multiplying a vector by a real number, which involves distributing that multiplication to each component of the vector.
How do you calculate the magnitude of a vector in 3D space?
-The magnitude of a vector is calculated by squaring each of its components, summing them up, and then taking the square root of the result.
What is the geometric interpretation of scalar multiplication?
-Geometrically, scalar multiplication gives a vector that is parallel to the original vector but with a scaled length. For example, multiplying by 2 gives a vector twice as long in the same direction.
What happens when you multiply a vector by a scalar of zero?
-Multiplying any vector by zero results in a zero vector, where every component of the vector is zero, indicating a vector that 'goes nowhere' and does not have a specific direction.
What is a unit vector and how is it defined?
-A unit vector is a vector that has a magnitude of one unit. It is often used to represent direction without regard to magnitude.
What are the standard unit vectors in 3D space and how are they denoted?
-The standard unit vectors in 3D space are î, ĵ, and k̂, which point one unit in the positive x, y, and z directions, respectively, and are denoted with a hat notation to indicate their unit length.
How can you express a vector as a linear combination of standard unit vectors?
-A vector can be expressed as a linear combination of standard unit vectors by multiplying each unit vector by the corresponding component of the original vector and summing these products.
What is the process for finding a unit vector in the direction of a given vector?
-To find a unit vector in the direction of a given vector, you divide the given vector by its magnitude, effectively normalizing it to a length of one unit.
Why are standard unit vectors mutually orthogonal?
-Standard unit vectors are mutually orthogonal because each one is perpendicular to the other two, meaning they lie along the axes at right angles to each other.
How do you find the unit vector for a given vector with components (3, 12, -4)?
-To find the unit vector for the given vector, you first calculate its magnitude, then divide each component of the vector by this magnitude. For (3, 12, -4), the magnitude is √(3² + 12² + (-4)²) = 13, so the unit vector is (3/13, 12/13, -4/13).
What is the significance of the zero vector in 3D space?
-The zero vector, with all components being zero, is unique in that it does not have a specific direction and represents a point at rest or with no displacement.

Outlines

00:00

📚 Introduction to Scalar Multiplication in 3D Space

This paragraph introduces the concept of scalar multiplication in the context of 3D space, using the example of a vector 'v' with components (3,1,2). Scalar multiplication involves multiplying a vector by a real number, which geometrically scales the vector's length while keeping it parallel to the original vector. The example given multiplies vector 'v' by 2, resulting in a new vector (6,2,4), which is twice as long as 'v' and points in the same direction. The paragraph also explains how to calculate the magnitude of a vector and demonstrates that multiplying by a scalar affects the magnitude accordingly, as shown with the calculation of the magnitude of 2 times vector 'v'.

05:02

📐 Understanding Unit Vectors and Standard Unit Vectors in R3

This paragraph delves into the concept of unit vectors, which are vectors with a magnitude of one. It introduces the standard unit vectors in 3D space: î, ĵ, and k̂, which point in the positive x, y, and z directions, respectively. The paragraph explains the hat notation used to denote unit vectors and contrasts it with the arrow notation used for general vectors. It also discusses the representation of vectors as linear combinations of standard unit vectors, providing examples of how to express vectors with components (2, -4, 1) and (3, 0, -5) in terms of î, ĵ, and k̂. The paragraph emphasizes the orthogonality and mutual perpendicularity of the standard unit vectors.

10:02

🧭 Calculating Unit Vectors in Specific Directions

The final paragraph focuses on how to find a unit vector in the direction of a given vector. It explains that to obtain a unit vector, one must divide the vector by its own magnitude. The process is illustrated with two examples: finding the unit vectors for vectors 'v' = (3, 12, -4) and 'w' = (4, -2, 1). The calculations involve determining the magnitude of each vector and then dividing each of its components by this magnitude. The resulting unit vectors, v̂ and ŵ, are presented with their simplified forms, demonstrating the method to ensure a vector has a unit length while maintaining the same direction as the original vector.

Mindmap

Keywords

💡Scalar Multiplication

Scalar multiplication is the process of multiplying a vector by a real number, resulting in a new vector whose components are each multiplied by that scalar. In the context of the video, this concept is used to demonstrate how the length of a vector changes when it is scaled by a scalar. For example, multiplying vector v by 2 results in a new vector with components (6, 2, 4), which is twice as long as the original vector v.

💡Magnitude

The magnitude of a vector, also referred to as its length, is a measure of the vector's size in Euclidean space. The magnitude is calculated using the square root of the sum of the squares of its components. In the video, the magnitude of vector v is found to be the square root of 14, which is used to illustrate how scalar multiplication affects the length of a vector.

💡Unit Vector

A unit vector is a vector with a magnitude of one. It is used to indicate direction without considering length. The video explains that any vector can be normalized to a unit vector by dividing it by its magnitude. For instance, if vector v has a magnitude of 5, then the unit vector in the direction of v, denoted as v-hat, is obtained by dividing v by 5.

💡Standard Unit Vectors

Standard unit vectors are vectors of unit length that point in the direction of the coordinate axes. In three-dimensional space (R3), these are represented as i-hat (1, 0, 0), j-hat (0, 1, 0), and k-hat (0, 0, 1). The video uses these vectors to demonstrate how any vector can be expressed as a linear combination of standard unit vectors.

💡Orthogonal

Orthogonality in the context of vectors means that two vectors are perpendicular to each other. The video mentions that the standard unit vectors i-hat, j-hat, and k-hat are mutually orthogonal, meaning each pair of these vectors is perpendicular, which is a fundamental property in vector algebra.

💡Zero Vector

The zero vector is a vector where all components are zero. It is unique in that it does not have a specific direction and its magnitude is zero. In the video, the concept of the zero vector is introduced when discussing the result of scalar multiplication of any vector by zero.

💡Hat Notation

Hat notation, or directed hat notation, is used to denote a unit vector. It is a convention where a caret (^) is placed above a letter to indicate that the vector is of unit length. For example, i-hat, j-hat, and k-hat are represented using this notation in the video to emphasize their unit magnitude.

💡Linear Combination

A linear combination of vectors is an expression formed by multiplying vectors by scalars and adding the results. The video demonstrates how any vector in R3 can be represented as a linear combination of the standard unit vectors, such as expressing the vector (2, -4, 1) as 2i-hat - 4j-hat + k-hat.

💡Direction

The direction of a vector is the orientation it points to in space. In the video, the concept of direction is used to explain how scalar multiplication affects a vector's length while maintaining its direction, and how unit vectors can be found in the same direction as any given vector by normalizing it.

💡Vector Normalization

Vector normalization is the process of converting a vector to a unit vector by dividing it by its magnitude. The video explains that to find a unit vector in the direction of a given vector, one must perform normalization, which is done by dividing each component of the vector by its magnitude.

Highlights

Introduction to the concept of scalar multiplication in 3D space.

Explanation of scalar multiplication as multiplying a vector by a real number.

Demonstration of scalar multiplication with an example of 2 times vector v.

Geometric interpretation of scalar multiplication affecting the magnitude of a vector.

Calculation of the magnitude of vector v and its scalar multiple.

Illustration of how scalar multiplication by 2 doubles the vector's length.

Discussion on the effect of scalar multiplication on the direction of a vector.

Examples of scalar multiplication with various scalars including negative values.

Clarification on the concept of a zero vector resulting from scalar multiplication by zero.

Introduction to unit vectors and their definition as vectors of one unit length.

Presentation of standard unit vectors in R3 and their special names i hat, j hat, and k hat.

Explanation of the orthogonality of standard unit vectors in 3D space.

Introduction to the notation for unit vectors and the concept of hat notation.

Method of expressing vectors as linear combinations of standard unit vectors.

Process of finding a unit vector in the direction of a given vector by dividing by its magnitude.

Examples of calculating unit vectors for given vectors v and w.

Final demonstration of finding unit vectors v hat and w hat with specific calculations.

Transcripts

Browse More Related Video

Unit Vectors | Physics with Professor Matt Anderson | M3-06

Unit Tangent Vector & Principal Unit Normal Vector (Calculus 3)

Vectors - Precalculus

Lec 1: Dot product | MIT 18.02 Multivariable Calculus, Fall 2007

What are Vector and Scalar Quantities?

Ch. 9.4 Vectors in Three Dimensions

Unit Vectors & Scalar Multiplication (in 3 dimensions)

Takeaways

Q & A

What is scalar multiplication in the context of 3D space?

How do you calculate the magnitude of a vector in 3D space?

What is the geometric interpretation of scalar multiplication?

What happens when you multiply a vector by a scalar of zero?

What is a unit vector and how is it defined?

What are the standard unit vectors in 3D space and how are they denoted?

How can you express a vector as a linear combination of standard unit vectors?

What is the process for finding a unit vector in the direction of a given vector?

Why are standard unit vectors mutually orthogonal?

How do you find the unit vector for a given vector with components (3, 12, -4)?

What is the significance of the zero vector in 3D space?