Ch. 9.4 Vectors in Three Dimensions
TLDRThis video script delves into the concept of vectors in three dimensions, drawing parallels with two-dimensional vectors and extending the principles to include a third variable. It covers the component form, magnitude calculation, and representation using standard unit vectors i, j, and k. The script also explains the dot product and introduces direction angles alpha, beta, and gamma, which a vector makes with the x, y, and z axes, respectively. The relationship between these angles and the vector's components is explored, emphasizing the property that the sum of the squares of the cosines of these angles equals one.
Takeaways
- 📚 The class is discussing Chapter 9.4, which focuses on vectors in three dimensions, extending the concepts from two-dimensional vectors.
- 📐 In linear algebra, vectors can be n-dimensional, but for calculus and practical purposes, the focus is on three dimensions, aligning with the three-dimensional nature of our world.
- 📍 The component form of a vector in three-dimensional space is similar to that in two dimensions, with an additional third term representing the z-coordinate.
- 🔢 The formula for the magnitude of a vector in three dimensions is an extension of the distance formula in two dimensions, involving the square root of the sum of the squares of its components.
- 📈 Standard unit vectors in three dimensions are i, j, and k, representing the x, y, and z directions respectively, in contrast to the two-dimensional i and j.
- 🔍 Vectors can be represented in terms of standard unit vectors, such as a vector with components (-2, 3, 1) can be written as -2i + 3j + k.
- 🔄 The dot product formula remains consistent across dimensions, calculated by multiplying corresponding components of two vectors and summing the results.
- 📐 The geometric representation of the dot product involves the lengths of the vectors and the cosine of the angle between them, which can be used to find the angle if it's unknown.
- 🧭 Direction angles of a vector are introduced, with a non-zero vector forming angles with the x, y, and z axes, represented by alpha, beta, and gamma respectively.
- 📐 The direction angles can be found using the components of the vector and their ratios to the vector's magnitude, such as cos(alpha) = v1 / magnitude of v.
- 🔄 A property of the direction cosines is that the sum of the squares of cos(alpha), cos(beta), and cos(gamma) equals 1, reflecting the vector's orientation in three-dimensional space.
Q & A
What is the main topic of Chapter 9.4 in the transcript?
-The main topic of Chapter 9.4 is vectors in three dimensions, extending the concepts from two-dimensional vectors to include the third variable.
How does the concept of vectors in three dimensions relate to those in two dimensions?
-The concept of vectors in three dimensions is an extension of two-dimensional vectors, where the same rules apply but with an additional third term to consider.
In linear algebra, what is the general term for the number of dimensions a vector can have?
-In linear algebra, vectors are considered to be n-dimensional, meaning they can have any number of terms, including an infinite number.
Why do we typically focus on three dimensions in calculus?
-We focus on three dimensions in calculus because we live in a three-dimensional world, and for pre-calculus classes, it is a practical approach to understanding the concepts.
What is the component form of a vector in three-dimensional space?
-The component form of a vector in three-dimensional space is given by the differences between the initial and terminal points' coordinates: (x1 - x0, y1 - y0, z1 - z0).
How is the magnitude of a vector in three dimensions calculated?
-The magnitude of a vector in three dimensions is calculated by squaring each component, summing them up, and taking the square root, which is an extension of the distance formula in two dimensions.
What are the standard unit vectors in three-dimensional space?
-The standard unit vectors in three-dimensional space are i (1, 0, 0) for the x-axis, j (0, 1, 0) for the y-axis, and k (0, 0, 1) for the z-axis.
How can a vector be represented using standard unit vectors in three dimensions?
-A vector can be represented as a sum of its components multiplied by the corresponding standard unit vectors, for example, a vector (-2, 3, 1) can be represented as -2i + 3j + k.
What is the formula for the dot product of two vectors in three dimensions?
-The dot product formula in three dimensions is the sum of the products of the corresponding components of the two vectors: v · u = (v1 * u1) + (v2 * u2) + (v3 * u3).
How can the angle between two vectors be found using the dot product?
-The angle between two vectors can be found using the geometric representation of the dot product: cos(theta) = (v · u) / (||v|| * ||u||), where theta is the angle and ||v|| and ||u|| are the magnitudes of the vectors.
What are the direction angles of a vector in three-dimensional space?
-The direction angles of a vector in three-dimensional space are the angles the vector makes with each of the coordinate axes, typically denoted as alpha (α) with the x-axis, beta (β) with the y-axis, and gamma (γ) with the z-axis.
How can the direction angles of a vector be related to its components and magnitude?
-The direction angles can be related to the vector's components and magnitude through the equations: v1 = ||v|| * cos(alpha), v2 = ||v|| * cos(beta), and v3 = ||v|| * cos(gamma).
What property do the direction cosines of a vector satisfy?
-The direction cosines of a vector satisfy the property that the sum of the squares of the cosines of the direction angles equals 1: cos^2(alpha) + cos^2(beta) + cos^2(gamma) = 1.
Outlines
📚 Introduction to 3D Vectors and Linear Algebra
This paragraph introduces the concept of vectors in three-dimensional space as an extension of two-dimensional vectors. It explains that the principles of vector operations in two dimensions can be applied to three dimensions with the addition of a third variable. The lecturer emphasizes that linear algebra considers vectors as n-dimensional, but for practical purposes in calculus and our three-dimensional world, the focus is on three dimensions. The component form of a vector in three space is discussed, along with how to calculate the magnitude of a vector using the distance formula extended to three dimensions. The paragraph also touches on the representation of vectors using standard unit vectors i, j, and k, and the formula for the dot product, which remains unchanged in three dimensions.
📐 Exploring Direction Angles and Properties of 3D Vectors
The second paragraph delves into the direction angles of a vector in three-dimensional space. It explains that a vector now forms angles with the x, y, and z axes, referred to as alpha, beta, and gamma respectively. The concept of projecting the vector onto the x-y plane and other planes to determine these angles is introduced. The relationship between the components of the vector and the cosine of these angles is established, with the formulae for calculating cosine of alpha, beta, and gamma provided. The paragraph concludes with the property that the sum of the squares of these cosines equals one, highlighting the geometric interpretation of these angles in relation to the vector's magnitude.
Mindmap
Keywords
💡Vectors
💡Three-Dimensional Geometry
💡Linear Algebra
💡Component Form
💡Magnitude
💡Standard Unit Vectors
💡Dot Product
💡Direction Angles
💡Cosine
💡Projection
💡Geometric Representation
Highlights
Introduction to vectors in three dimensions, extending concepts from two-dimensional geometry to include a third variable.
Vectors can be n-dimensional in linear algebra, applicable to any number of dimensions.
Focus on three-dimensional vectors for calculus, as it relates to our three-dimensional world.
Component form of a vector in three space includes an extra variable compared to two space.
Magnitude of a vector in three dimensions calculated using an extension of the distance formula.
Standard unit vectors in three dimensions include i, j, and k, each pointing in the respective axis direction.
Example given to represent a vector in terms of standard unit vectors in three dimensions.
Dot product formula remains consistent across dimensions, calculated by multiplying corresponding elements.
Geometric representation of the dot product involves the lengths of vectors and the cosine of the angle between them.
Introduction of direction angles for a vector in three dimensions: alpha, beta, and gamma.
Direction angles represent the angles a vector makes with the x, y, and z axes respectively.
Explaining how to find the direction angles using the components of the vector and their magnitude.
Property of direction cosines where the sum of the squares of cosines equals one.
Practical application of direction angles in understanding the orientation of a vector in three-dimensional space.
The relationship between the vector components and the cosine of their respective direction angles.
Concept of projecting a vector onto different planes to understand the angles formed with each axis.
Summary of the process to determine the direction angles and their significance in vector analysis.
Transcripts
Browse More Related Video

Unit Vectors | Physics with Professor Matt Anderson | M3-06

Unit Vectors & Scalar Multiplication (in 3 dimensions)
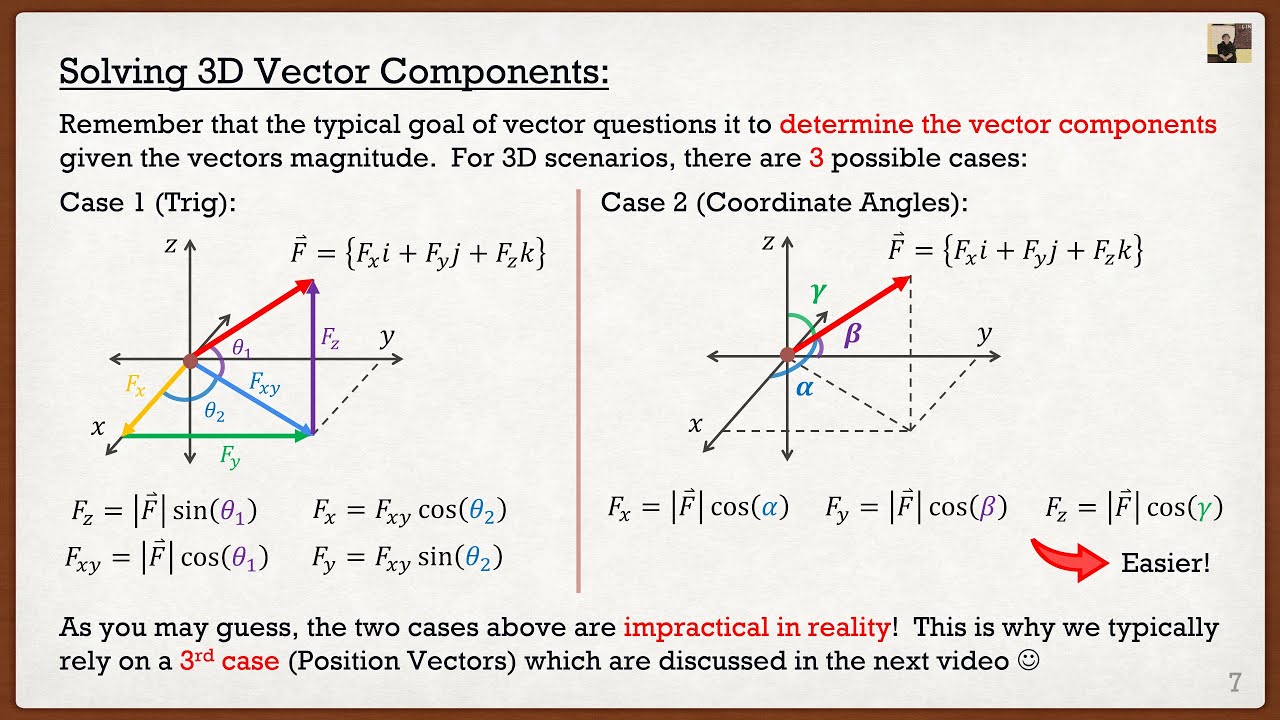
Engineering Mechanics: Statics Lecture 4 | Cartesian Vectors in 3D
Lec 1: Dot product | MIT 18.02 Multivariable Calculus, Fall 2007

Vectors - Precalculus

How To Find The Resultant of Two Vectors
5.0 / 5 (0 votes)
Thanks for rating: