Calculus 2: Polar Coordinates (Video #30) | Math with Professor V

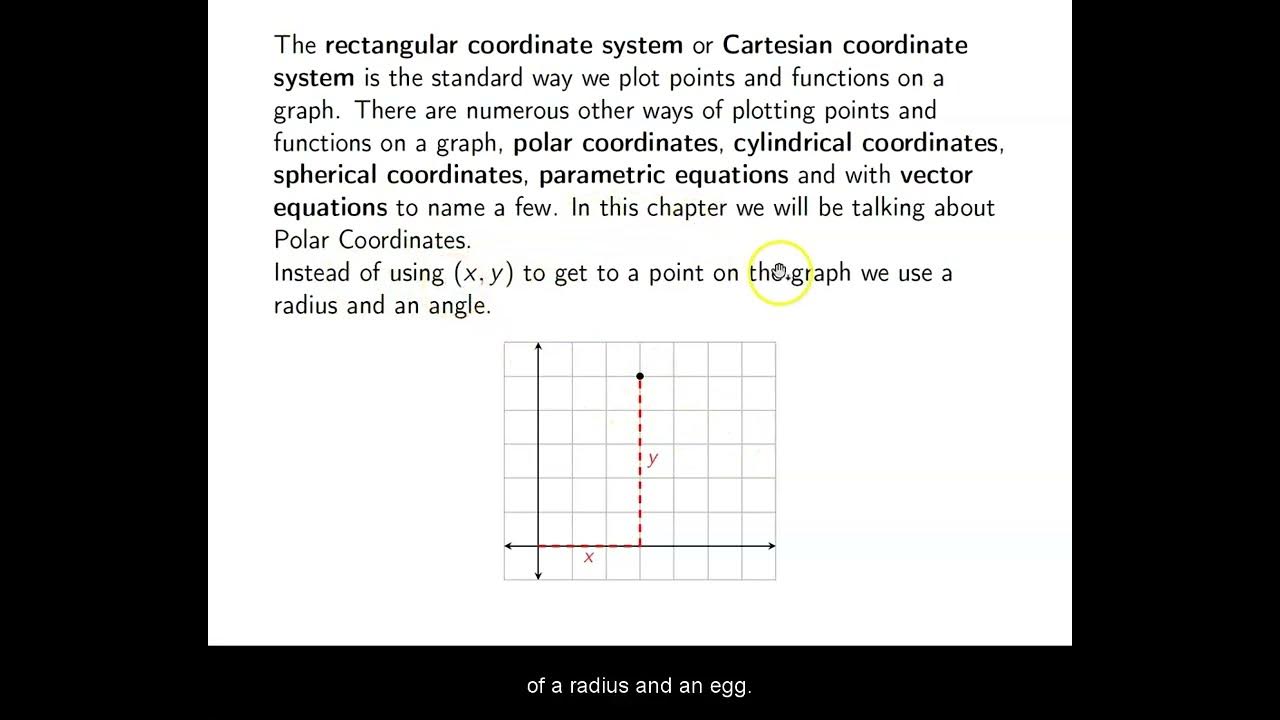
This paragraph introduces the concept of polar coordinates as an alternative to the Cartesian coordinate system for defining points in a two-dimensional space. The polar coordinate system uses a pole, analogous to the origin in Cartesian coordinates, and a polar axis, typically aligned with the positive x-axis. The location of a point P is determined by two values: r, the distance from the pole to the point, and theta, the angle measured from the polar axis to the line segment connecting the pole and point P. The paragraph explains that while the Cartesian system is well-known, the polar system can be more convenient in certain situations, such as when dealing with problems involving circular symmetry.

The second paragraph demonstrates how to plot points in the polar coordinate system. It explains that the radius (r) is listed first, followed by the angle (theta). The process involves determining the angle's quadrant and then measuring the radius from the pole. The paragraph provides examples of plotting points with positive and negative radii, illustrating how a negative radius results in a point located in the opposite direction along the angle from the pole. It also introduces the concept that polar coordinates are not unique, meaning a single point can be represented by multiple sets of polar coordinates.

This paragraph delves into the mathematical relationship between rectangular (Cartesian) and polar coordinates, explaining how to convert between the two systems. It outlines the formulas for converting x and y coordinates to r and theta, and vice versa. The explanation includes the use of trigonometric ratios and the Pythagorean theorem to derive the formulas for r and theta. The paragraph also covers how to determine the correct quadrant for theta when converting from rectangular to polar coordinates.

The fourth paragraph provides a step-by-step example of converting a specific point with rectangular coordinates (1, -2) to polar coordinates. It calculates the radius (r) using the Pythagorean theorem and determines the angle (theta) using the tangent function. The summary includes the process of finding the reference angle and adjusting theta to ensure it falls within the correct quadrant. The paragraph concludes with multiple options for expressing the final polar coordinates, considering different conventions for the angle's range.

The fifth paragraph presents an example of converting a point given in polar coordinates (r = 1, theta = 7π/4) to rectangular coordinates. It simplifies the conversion by using the relationships x = r * cos(theta) and y = r * sin(theta), resulting in exact values for x and y. The summary highlights the ease of this conversion compared to the previous example and emphasizes the importance of understanding these relationships for future applications.

This paragraph discusses the process of converting polar equations to Cartesian equations, which can be useful for graphing and analyzing curves in the Cartesian coordinate system. It provides an example of converting the equation r * cos(theta) to a Cartesian equation by isolating x and replacing r with its equivalent expression in terms of x and y. The summary explains how to manipulate the equation to eliminate r and theta, resulting in a Cartesian equation that can be easily graphed.

The sixth paragraph explores the concept of finding the slope of the tangent line to a polar curve by treating the polar curve as a set of parametric equations. It explains the process of differentiating the parametric equations with respect to the parameter theta and then taking the ratio of the derivatives to find dy/dx. The paragraph provides a specific example where the polar curve r = 2 - sin(theta) is given, and it shows the steps to find the slope of the tangent line at theta = π/3.

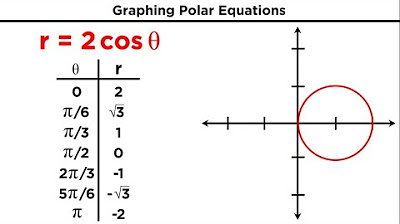
The final paragraph provides an overview of common polar equations and their graphs, such as lines, circles, cardioids, limassons, and roses. It emphasizes the importance of understanding these equations for applications in calculus, especially when dealing with areas and lengths. The paragraph also offers a quick example of graphing the polar equation r = 1 - 3cos(theta), identifying it as a limaçon with an inner loop. The summary includes a step-by-step approach to plotting the curve by creating a table of theta and r values and encourages the viewer to practice plotting for a better understanding of the curve's shape.

The concluding paragraph summarizes the lesson on polar coordinates and their applications in calculus. It encourages viewers to store the information for future reference and to engage with the content by liking, subscribing, and sharing the video. The paragraph also teases upcoming lessons on integration and polar calculus, inviting the audience to stay tuned for more educational content.