Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy
TLDRThe video script discusses the conversion between polar and rectangular (Cartesian) coordinates, two methods for specifying a point in two dimensions. It emphasizes that while Cartesian coordinates use x and y to indicate horizontal and vertical distances, polar coordinates use an angle and a radius to describe direction and distance from the origin. The script provides an intuitive explanation and a step-by-step conversion of a polar coordinate (4, 150 degrees) to Cartesian coordinates (x = -3.46, y = 2), using the formulas x = r * cos(θ) and y = r * sin(θ). It also touches on converting equations, specifically transforming the equation of a circle (x^2 + y^2 = 4) into polar coordinates, resulting in r = 2, showcasing the simplicity of representing a circle in polar form. The video concludes by hinting at further conversions and the exploration of negative radius implications in polar coordinates.
Takeaways
- 📐 The video discusses the conversion between polar and rectangular (Cartesian) coordinates, emphasizing that both are methods to specify a point in two dimensions.
- 🧭 Cartesian coordinates are described with x indicating horizontal distance and y for vertical distance from a reference point.
- 🌐 Polar coordinates use an angle to indicate direction and a radius (r) to indicate the distance from the origin in that direction.
- 🤔 The video encourages developing intuition for both coordinate systems, as some functions are better described in polar coordinates, while others are more straightforward in Cartesian.
- 📈 The script provides a step-by-step guide to convert a given polar coordinate (4, 150 degrees) to Cartesian coordinates, using the formulas x = r * cos(θ) and y = r * sin(θ).
- 📊 The video demonstrates the conversion process with an example, calculating the Cartesian coordinates to be approximately (-3.46, 2) for the given polar coordinate.
- ⭕ The script explains how to convert the equation of a circle, x² + y² = 4, into polar coordinates, resulting in r² = 4, which simplifies to r = 2, indicating a circle with a radius of 2 units.
- 📚 The importance of understanding the relationship between x² + y² and r², as well as the tangent of theta (tan(θ)) being equal to y/x, is highlighted for converting equations between coordinate systems.
- 📉 The video also covers converting the equation x² + y² = 9(y/x)² into polar coordinates, resulting in r = ±3tan(θ), illustrating the concept of a negative radius and its effect on the direction of the point.
- 🔍 The script suggests that memorizing key equations for polar coordinates can be helpful, but also emphasizes the value of understanding and re-proving them for a deeper grasp.
- 📚 The video ends with a teaser for the next part, indicating more examples and explanations will be provided in a continuation of the lesson.
Q & A
What are polar and rectangular coordinates?
-Polar coordinates specify a point in two dimensions using an angle and a distance from the origin, while rectangular (or Cartesian) coordinates use horizontal and vertical distances from the origin.
How do you convert polar coordinates to Cartesian coordinates?
-To convert polar coordinates (r, θ) to Cartesian coordinates (x, y), use the formulas: x = r * cos(θ) and y = r * sin(θ).
What is the intuition behind polar coordinates?
-In polar coordinates, the angle θ tells you the direction to point in, and the radius r tells you how far to walk in that direction.
Why might some functions be better described in polar coordinates?
-Some functions are more naturally expressed in polar coordinates, particularly those involving circles or radial symmetry, as they can simplify the equations.
How do you convert the polar coordinate (4, 150 degrees) to Cartesian coordinates?
-First, calculate x = 4 * cos(150 degrees) = -3.46 and y = 4 * sin(150 degrees) = 2. The Cartesian coordinates are (-3.46, 2).
What does the equation x² + y² = 4 represent in polar coordinates?
-In polar coordinates, x² + y² = r², so the equation x² + y² = 4 converts to r² = 4, which simplifies to r = 2. This represents a circle with radius 2.
How do you identify x² + y² in polar coordinates?
-In polar coordinates, x² + y² is equal to r², derived from the Pythagorean theorem.
What does the equation x² + y² = 9(y/x)² convert to in polar coordinates?
-Using the relationships x² + y² = r² and y/x = tan(θ), the equation x² + y² = 9(y/x)² converts to r² = 9(tan(θ))², and further to r = 3|tan(θ)|.
How can negative radii be interpreted in polar coordinates?
-Negative radii in polar coordinates indicate moving in the opposite direction of the angle. For example, a radius of -2 at an angle θ means moving 2 units in the direction opposite to θ.
What are the key equations to remember for converting between Cartesian and polar coordinates?
-The key equations are: x = r * cos(θ), y = r * sin(θ), x² + y² = r², and tan(θ) = y/x.
Outlines
📐 Understanding Polar and Cartesian Coordinates
The script begins with an explanation of the tools used to convert between polar and rectangular (Cartesian) coordinates. The narrator emphasizes that both coordinate systems are methods to specify a point in two dimensions, with Cartesian coordinates using x and y to indicate horizontal and vertical distances, respectively, and polar coordinates using an angle and a radius. The narrator also discusses the intuition behind these systems, mentioning that some functions are more easily described in polar coordinates, while others are better suited for Cartesian coordinates. An example is given to convert a polar coordinate (4, 150 degrees) to Cartesian coordinates (x, y), using the formulas x = r cos(theta) and y = r sin(theta), resulting in x ≈ -3.46 and y ≈ 2. This conversion is visually demonstrated, and the narrator confirms that the visual estimation aligns with the calculated values.
📚 Converting Equations Between Polar and Cartesian Coordinates
The second paragraph delves into converting equations from Cartesian to polar coordinates and vice versa. The narrator starts by converting the equation x^2 + y^2 = 4 into polar coordinates, recognizing it as a circle. Using the relationships x^2 + y^2 = r^2, y = r sin(theta), and x = r cos(theta), the equation simplifies to r = 2, indicating a circle with a radius of 2 in all directions. The narrator also discusses the significance of a constant radius in polar coordinates and its representation of a circle. The paragraph continues with another conversion, x^2 + y^2 = 9(y/x)^2, which simplifies to r = ±3tan(theta), illustrating the pattern matching between Cartesian and polar forms. The narrator emphasizes the concept of a negative radius, explaining that it represents a direction opposite to that of a positive radius. The paragraph concludes with the intention to continue the discussion in the next video.
Mindmap
Keywords
💡Polar Coordinates
💡Cartesian Coordinates
💡Conversion
💡Angle
💡Radius
💡SOH-CAH-TOA
💡Function Conversion
💡Pythagorean Theorem
💡Visualization
💡Degrees vs. Radians
Highlights
Equipping with tools to convert between polar and rectangular coordinates.
Intuition for Cartesian coordinates: x-coordinate for left-right distance and y-coordinate for up-down distance.
Polar coordinates described: angle for direction and radius for distance.
Different functions are better described in polar or Cartesian coordinates.
Quick problem-solving using the tools built for coordinate conversion.
Conversion of polar coordinate (4, 150 degrees) to Cartesian coordinates.
Visualization of polar coordinates by drawing and understanding the angle.
Conversion process using the formulas x = r*cosine(theta) and y = r*sine(theta).
Calculating Cartesian coordinates with the cosine and sine of 150 degrees.
Intuition confirmed with calculated Cartesian coordinates (x ≈ -3.46, y ≈ 2).
Transition from polar to Cartesian coordinates demonstrated.
Introduction to converting functions between polar and Cartesian coordinates.
Conversion of the equation x^2 + y^2 = 4 to polar coordinates, revealing a circle.
Use of Pythagorean theorem and trigonometric identities for conversion.
Memorization of key equations for polar coordinates is suggested for exams.
Graphical representation of r = 2 as a circle in polar coordinates.
Exploration of the equation x^2 + y^2 = 9*(y/x)^2 and its conversion to polar coordinates.
Understanding negative radius in polar coordinates and its effect on direction.
Final conversion result r = 3*tan(theta) and its implications.
Transcripts
Browse More Related Video

Lesson 14 - Polar Equations (Calculus 2 Tutor)
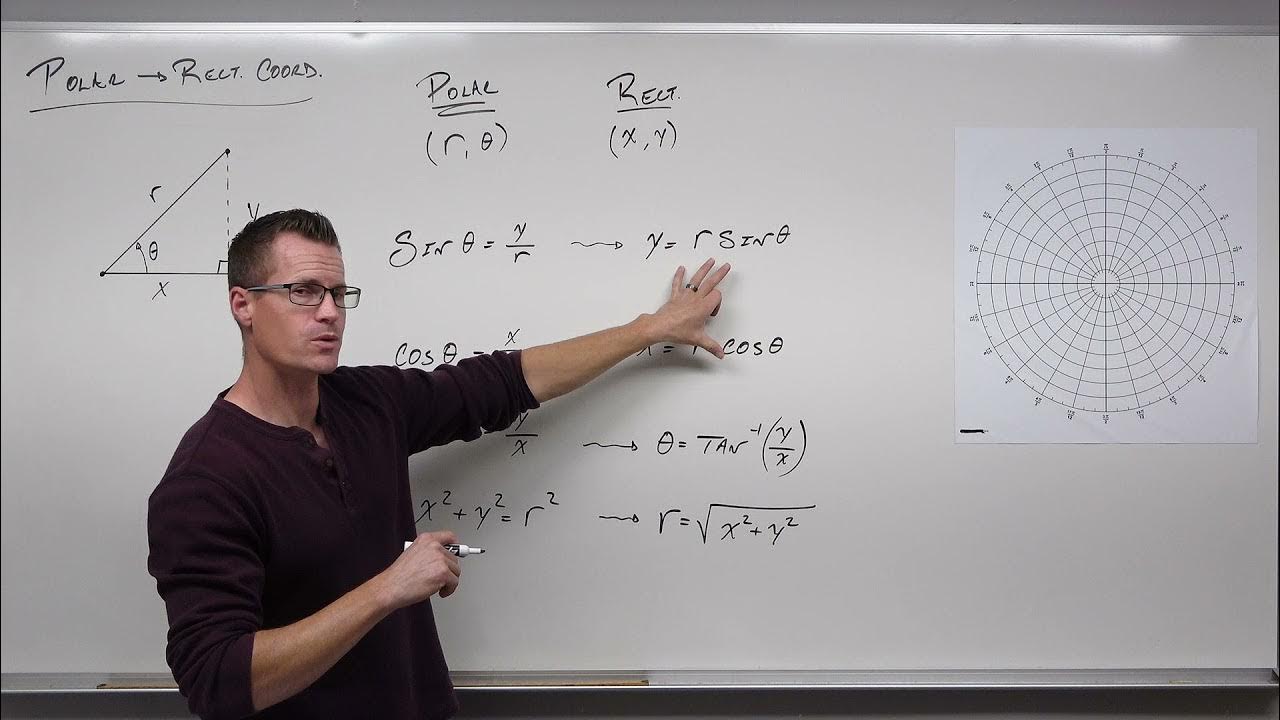
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy
Ch. 8.1 Polar Coordinates

How to Convert From Rectangular Equations to Polar Equations (Precalculus - Trigonometry 39)

Polar coordinates 1 | Parametric equations and polar coordinates | Precalculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: