Polar Curves

RH Mathematics

10 Feb 202228:25

EducationalLearning

32 Likes 10 Comments

TLDRThis video offers an introduction to polar coordinates, contrasting them with rectangular coordinates and explaining their applications. It covers the conversion between polar (r, θ) and rectangular (x, y) coordinates using trigonometric relationships. The presenter demonstrates how to graph basic polar curves, such as circles and rose curves, and discusses the calculus of polar curves, including finding slopes and tangents. Examples of polar equations are provided, along with their graphical representations and applications in solving problems related to slopes and distances in polar coordinates.

Takeaways

📚 The video introduces polar coordinates, explaining the difference between rectangular and polar coordinates and their applications.
📐 Polar coordinates are represented by r (distance from the origin) and θ (angle from the positive x-axis), contrasting with rectangular coordinates (x, y).
🔍 To convert rectangular coordinates to polar, use the formulas r = sqrt(x^2 + y^2) and θ = arctan(y/x), though finding θ can be more complex than for standard angles.
📉 The video provides examples of converting specific points from rectangular to polar coordinates, demonstrating the process and the importance of considering the correct quadrant for θ.
📈 The relationship between x, y, r, and θ is explored, with formulas x = r cos(θ) and y = r sin(θ) being key for converting between coordinate systems.
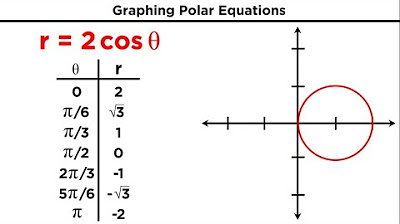
🌐 The video discusses the graphing of polar curves, explaining that r = a represents a circle with radius a, and r = cos(θ) or r = sin(θ) traces out a semicircle.
📊 The concept of lines in polar coordinates is introduced, with θ = constant representing lines that extend infinitely in the direction of θ.
🌹 The video demonstrates how to graph more complex polar curves, such as r = sin(3θ) and r = cos(4θ), which create rose curves with multiple petals.
🔢 The video covers basic calculus in polar coordinates, focusing on finding slopes and tangent lines, using derivatives dy/dx = y'/x' where y = r sin(θ) and x = r cos(θ).
📍 The video concludes with practical problems, such as finding the maximum distance from the origin for a given polar curve and determining the value of θ for a point with a specific y-coordinate.

Q & A

What is the main topic of the video?
-The main topic of the video is polar coordinates and polar curves, explaining the concepts and how they relate to rectangular coordinates.
What are the two main components of a polar coordinate system?
-The two main components of a polar coordinate system are the radius (r), which measures the distance from the origin, and the angle (theta), which indicates the direction from the origin.
How can you convert rectangular coordinates (x, y) to polar coordinates (r, theta)?
-To convert rectangular coordinates to polar coordinates, you can use the formulas r = √(x² + y²) and theta = arctan(y/x). However, note that theta can vary depending on the quadrant.
What is the relationship between x and r in polar coordinates?
-In polar coordinates, x is related to r by the formula x = r * cos(theta).
What is the relationship between y and r in polar coordinates?
-In polar coordinates, y is related to r by the formula y = r * sin(theta).
How does the video describe the usefulness of polar coordinates in real-life scenarios?
-The video uses the analogy of giving directions to a gas station. Rectangular coordinates are like giving specific street addresses, while polar coordinates are like describing the distance and direction from a known point.
What are some basic polar equations that the video discusses?
-The video discusses basic polar equations such as r = 2, r = cos(theta), r = sin(theta), and r = theta, which represent circles and lines in polar coordinates.
How does the video explain the graph of r = 2 sin(3θ)?
-The graph of r = 2 sin(3θ) is described as a rose curve with three petals, traced out over the interval from 0 to π.
What is the significance of the theta step in graphing polar equations on a calculator?
-The theta step is important because it determines the resolution of the graph. A smaller step size, like π/24, can provide a more detailed graph, especially for complex polar equations.
How does the video approach finding the slope of a polar curve at a specific point?
-The video explains that the slope of a polar curve at a specific point is found by calculating dy/dx = y'/x', where y = r * sin(theta) and x = r * cos(theta), and then evaluating these derivatives at the given theta value.
What is the method used in the video to find the largest distance from the origin in a polar curve?
-The video uses the method of finding the maximum value of the absolute value of r by setting the derivative of r with respect to theta equal to zero and solving for theta, then evaluating r at those points.
How does the video solve for the value of theta that corresponds to a point on a polar curve with a specific y-coordinate?
-The video sets up the equation r * sin(theta) = y, where y is the given y-coordinate, and solves for theta by setting the equation equal to zero and using a calculator to find the roots.

Outlines

00:00

📚 Introduction to Polar Coordinates

The script begins with an introduction to polar coordinates, contrasting them with the more familiar rectangular coordinates. The instructor explains that polar coordinates are based on the distance 'r' from the origin and the angle 'theta' from the positive x-axis. An example is given to illustrate the conversion from rectangular coordinates (x=3, y=4) to polar coordinates using trigonometry to find 'theta'. The importance of understanding both coordinate systems is emphasized, as each has its own practical applications, such as giving directions versus exact addresses.

05:01

📐 Formulas and Examples for Polar Coordinates

This section delves into the mathematical relationships between rectangular (x, y) and polar (r, theta) coordinates. The formulas x = r * cos(theta) and y = r * sin(theta) are introduced to convert from polar to rectangular coordinates. Conversely, r is found using the Pythagorean theorem, and theta can be determined using the inverse tangent function. The script provides examples to demonstrate these calculations, including finding polar coordinates for points with given rectangular coordinates and vice versa.

10:03

📉 Graphing Basic Polar Curves

The script moves on to discuss the graphical representation of polar curves, starting with simple examples like r = 2, which represents a circle with a radius of two units. It then describes more complex curves, such as r = cos(theta) and r = 2 * sin(theta), explaining how these equations trace out specific shapes on the polar graph. The instructor notes the difference in the way these curves are traced between 0 to pi and 0 to 2pi, highlighting the importance of understanding the interval over which the curve is drawn.

15:04

🤔 Analyzing Polar Curves with Calculus

Here, the script introduces the application of calculus to polar curves, focusing on finding slopes and understanding the behavior of the curves. The derivative of r with respect to theta is used to calculate the slope of the curve at a given point, exemplified by finding the slope of the curve r = 2 * theta at theta = pi. The concept of vertical tangents is also explored, where the derivative of x with respect to theta equals zero, causing the slope of the curve to become undefined.

20:06

🔍 Maximizing Distance and Finding Specific Points

The script presents problems involving the maximization of distance from the origin in polar coordinates and finding specific points on the curve. It explains how to use the derivative to find the maximum value of r and how to calculate the distance for given theta values. An example is provided to find the largest distance from the origin for a given polar equation, as well as how to find the value of theta corresponding to a point with a y-coordinate of one.

25:07

🎓 Conclusion and Final Thoughts

In the final paragraph, the script wraps up the lesson with a summary of the key points covered in the video. It emphasizes the importance of understanding both the graphical and calculus-based aspects of polar coordinates. The instructor thanks the viewers for watching and encourages them to apply the concepts learned in this video to further their understanding of polar curves.

Mindmap

Keywords

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system where each point on a plane is determined by a distance from a reference point, known as the origin, and an angle from a reference direction. In the video, polar coordinates are introduced as an alternative to the more traditional rectangular (Cartesian) coordinates, emphasizing their use in scenarios where radial distance and angular orientation are more intuitive, such as in describing the location of a gas station 'half a mile that way'.

💡Rectangular Coordinates

Rectangular coordinates, also known as Cartesian coordinates, are a system where each point on a plane is defined by an ordered pair of numbers indicating how far the point is along two perpendicular axes, typically x and y. The script contrasts rectangular coordinates with polar coordinates, using the example of giving directions to a gas station by street names ('the corner of 620 and Cavalier Drive'), which is akin to specifying exact locations on a grid.

💡Theta (θ)

Theta, symbolized by the Greek letter θ, represents the angle in polar coordinates that a point makes with the reference direction, usually the positive x-axis. In the video, theta is used to describe the direction of a point from the origin, and it is calculated using trigonometric relationships, such as in the example where 'tan(theta) = y/x' to find the angle for the point (3,4).

💡R

In polar coordinates, r represents the radial distance from the origin to the point of interest. The video explains that r is analogous to stating how far away a location is, such as 'five units away from the origin', and it is a fundamental component in defining a point's position in polar coordinates.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right-angled triangles. The video mentions trigonometry in the context of finding the angle theta for a given point in rectangular coordinates, using the tangent function, which is 'tan(theta) = opposite/adjacent'.

💡Polar Curves

Polar curves are curves plotted in the polar coordinate system, defined by an equation that relates r and theta. The script discusses various polar equations, such as r = 2, which represents a circle, and r = cos(theta), which traces out a specific type of curve, illustrating the concept with examples and their graphical representations.

💡Graphing Calculator

A graphing calculator is an electronic device used to graph functions and equations, often used in mathematical and scientific contexts. The video mentions using a graphing calculator to plot and understand the shapes of polar curves, such as 'r = sin(3θ)', and to find specific points or properties of the curves, like the length of a petal in a rose curve.

💡Rose Curve

A rose curve is a type of polar curve characterized by its petal-like appearance, resulting from equations of the form r = a * sin(k * theta) or r = a * cos(k * theta), where 'a' and 'k' are constants. The video describes rose curves with different numbers of petals based on the value of 'k', such as a rose curve with three petals for 'r = sin(3θ)'.

💡Slope

In the context of the video, slope refers to the rate of change of one variable with respect to another, specifically the derivative of y with respect to x in a polar curve. The script explains how to calculate the slope of a polar curve at a given point using derivatives, such as dy/dx = y' / x', and provides an example with the curve r = 2 * theta at theta = π.

💡Tangent Line

A tangent line is a straight line that touches a curve at a single point without crossing it. The video discusses the conditions for a tangent line to be horizontal or vertical on a polar curve, which occurs when the derivative x' equals zero for a vertical tangent, indicating a sharp turn in the curve.

Highlights

Introduction to polar coordinates as an alternative to rectangular coordinates.

Explanation of the polar coordinate system with r representing the distance from the origin and theta as the angle.

Conversion from rectangular to polar coordinates using trigonometry, demonstrated with an example.

Use of inverse tangent to find the angle theta in polar coordinates.

Illustration of the difference between describing locations using rectangular and polar coordinates with a real-world analogy.

Derivation of formulas relating x, y, r, and theta in both rectangular and polar coordinate systems.

Calculation of polar coordinates from rectangular coordinates using the Pythagorean theorem.

Graphical representation of polar curves, such as circles and lines, in the coordinate plane.

Explanation of how polar equations like r = a, r = cos(theta), and r = sin(theta) trace out different shapes.

Demonstration of how to graph basic polar curves and the importance of theta step in polar graphing.

Introduction to more complex polar curves like roses and spirals, and their graphical representation.

Use of graphing calculator to visualize and analyze polar equations like r = sin(3theta) and r = cos(4theta).

Calculus application in polar coordinates, finding the slope of a polar curve using derivatives.

Method to determine horizontal and vertical tangents on polar curves by setting derivatives equal to zero.

Strategy for finding the largest distance from the origin on a polar curve using the closed interval test.

Example of finding the value of theta for a given y-coordinate on a polar curve using calculus.

Conclusion summarizing the key points covered in the video on polar coordinates and their applications.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 9.7

Calculus 2: Polar Coordinates (Video #30) | Math with Professor V

Polar Coordinates Basic Introduction, Conversion to Rectangular, How to Plot Points, Negative R Valu

Polar Coordinates and Graphing Polar Equations

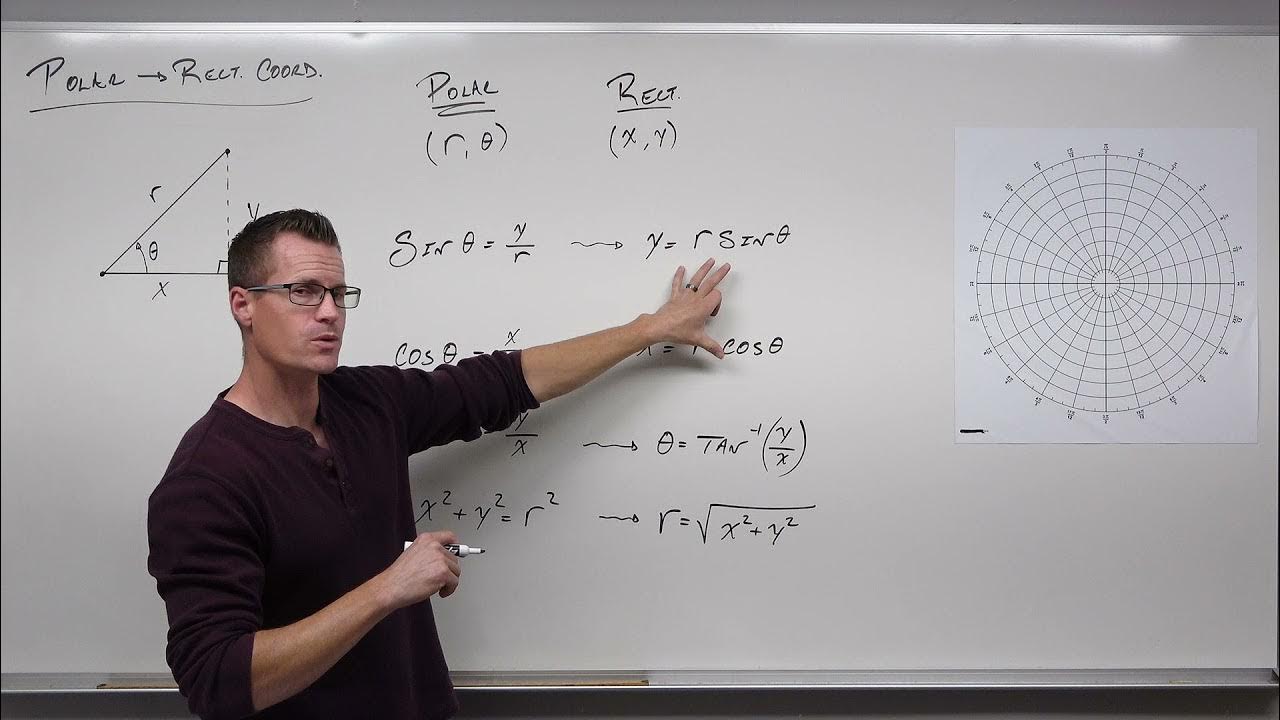
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Related Tags

Polar Coordinates Calculus Lessons Trigonometry Graphing Theta Values Rectangular vs Polar Curve Analysis Slope Calculation Rose Curves Distance Maximization