Precalculus: Polar Coordinates (Section 9.1) | Math with Professor V

Math with Professor V

23 Apr 202022:58

EducationalLearning

32 Likes 10 Comments

TLDRThis video introduces polar coordinates, a system for describing points in two-dimensional space using radius and angle. It explains how to plot points with polar coordinates, the concept of non-uniqueness in polar representation, and the relationship between polar and Cartesian coordinates. The video also covers formulas for converting between the two systems and demonstrates how to apply these conversions to various examples. Additionally, it explores how to rewrite equations in polar form and vice versa, providing a foundational understanding of polar coordinates for further mathematical exploration.

Takeaways

📍 Polar coordinates are represented as \( R, \theta \) where \( R \) is the distance from the pole (origin) to a point, and \( \theta \) is the angle formed with the polar axis.
📐 The polar axis is typically aligned with the positive x-axis in Cartesian coordinates, and \( \theta \) can be measured in degrees or radians.
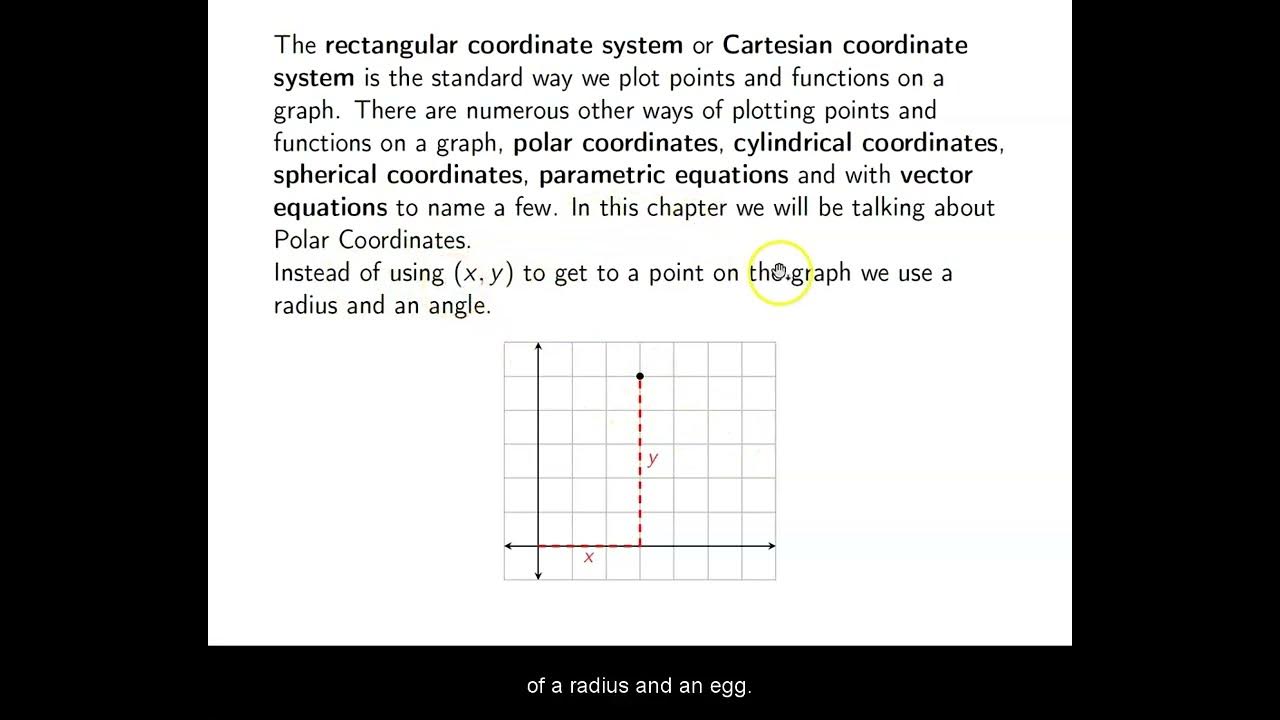
🔍 Polar coordinates provide an alternative way to describe points in two-dimensional space, beyond the Cartesian \( x, y \) system.
📉 When \( R \) is negative, the point is located in the opposite direction of the angle \( \theta \) from the pole.
🔄 Polar coordinates can be non-unique, meaning there may be multiple ways to represent the same point using different \( R \) and \( \theta \) values.
🔢 The conversion between polar and rectangular coordinates is facilitated by the formulas \( x = R \cdot \cos(\theta) \) and \( y = R \cdot \sin(\theta) \).
↔️ To convert from rectangular to polar, use \( R^2 = x^2 + y^2 \) and \( \tan(\theta) = y/x \), provided \( x \neq 0 \).
📈 The relationship between polar and Cartesian coordinates can be visualized through a right triangle formed by the point \( P \), the pole, and the projection of \( P \) onto the x-axis.
📊 The tangent function has a vertical asymptote at \( \theta = \pi/2 \) radians (90 degrees), where the denominator becomes zero in the \( \tan(\theta) = y/x \) formula.
🔄 Understanding the conversion formulas is crucial for solving problems that involve switching between polar and rectangular coordinate systems.
📚 The script concludes with an introduction to graphing in polar coordinates, which will be further explored in a subsequent video.

Q & A

What are polar coordinates and how are they represented?
-Polar coordinates are a two-dimensional coordinate system where each point is determined by a distance from a reference point, called the pole, and an angle from a reference direction, typically the positive x-axis. They are represented in the form R, comma theta (R, θ), where R is the radial distance and θ is the angle.
How do you plot a point with polar coordinates (R, θ)?
-To plot a point with polar coordinates, first locate the angle θ on the polar axis, starting from the positive x-axis. Then, count out the radial distance R from the pole in the direction of the angle θ to find the point.
What does a negative radius in polar coordinates indicate?
-A negative radius in polar coordinates indicates that the point is located on the opposite side of the pole from the angle θ, at the same distance but in the opposite direction.
Can polar coordinates be non-unique for a given point?
-Yes, polar coordinates can be non-unique for a given point. There can be more than one way to express a point in polar coordinates, especially when considering angles that are coterminal or when adding full revolutions (2π) to the angle.
How can you represent a point with polar coordinates where the radius is positive but the angle is negative?
-To represent a point with a positive radius and a negative angle, you can either sweep out a negative angle in a clockwise direction from the positive x-axis or subtract 2π from the original positive angle to get a negative angle that points to the same location.
What is the relationship between polar coordinates (R, θ) and rectangular coordinates (X, Y)?
-The relationship between polar and rectangular coordinates can be described by the following formulas: X = R * cos(θ) and Y = R * sin(θ). Conversely, R² = X² + Y² and tan(θ) = Y / X, provided X is not zero.
How do you convert rectangular coordinates to polar coordinates?
-To convert from rectangular coordinates (X, Y) to polar coordinates (R, θ), calculate R as the square root of the sum of the squares of X and Y (R = √(X² + Y²)). To find θ, use the arctangent of Y/X, keeping in mind the quadrant in which the point lies to determine the correct angle.
What is the significance of the point P in the context of converting between polar and rectangular coordinates?
-Point P is significant because it has both polar coordinates (R, θ) and rectangular coordinates (X, Y). It serves as an example to illustrate the conversion process between the two coordinate systems.
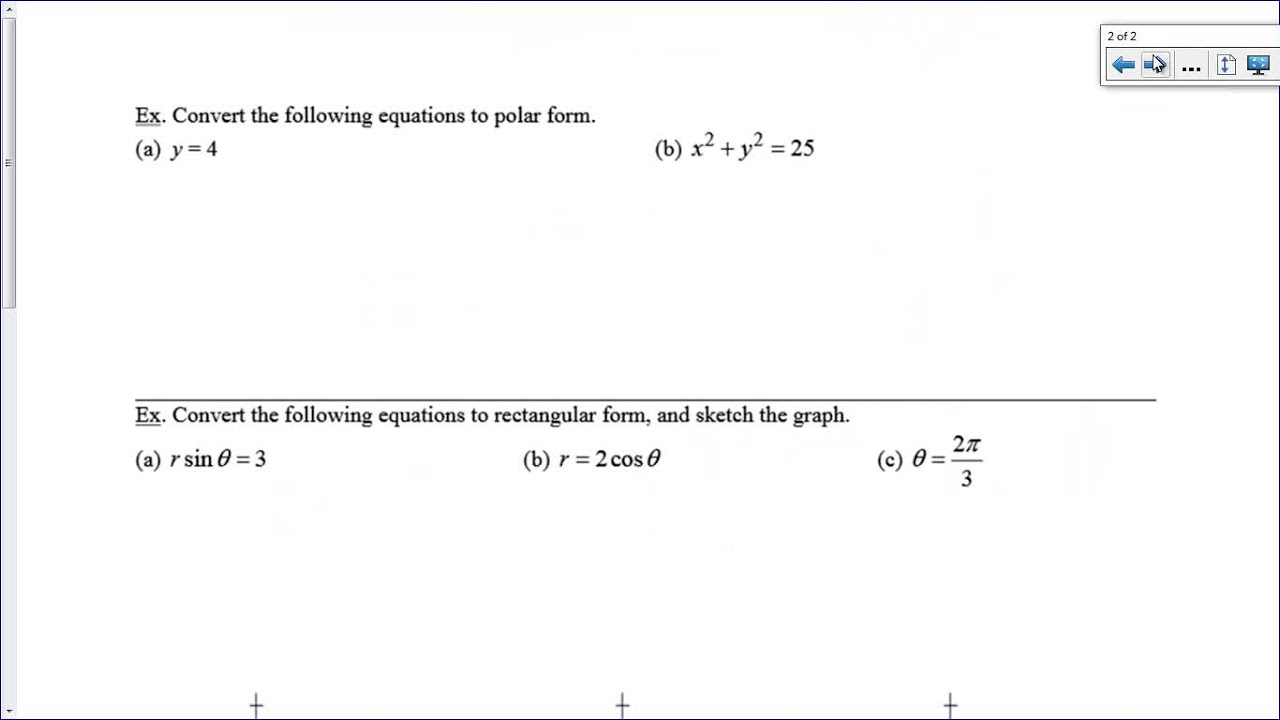
How can you switch equations from rectangular to polar coordinates?
-To switch equations from rectangular to polar coordinates, replace x with R * cos(θ) and y with R * sin(θ), and then simplify the equation, if possible, by dividing by R or using the identities R² = X² + Y².
What is the graphical representation of the equation R = sin(θ) - cos(θ) in rectangular coordinates?
-The equation R = sin(θ) - cos(θ) in rectangular coordinates represents a circle. After multiplying through by R and simplifying, it can be rewritten in the standard form of a circle's equation, (X - h)² + (Y - k)² = r², where (h, k) is the center and r is the radius.
Can you provide an example of converting a polar equation to a rectangular equation and vice versa?
-An example of converting a polar equation to a rectangular equation is the equation R = 2, which translates to X² + Y² = 4 in rectangular coordinates. Conversely, converting the rectangular equation X² + Y² = 4 to polar coordinates would involve recognizing that R² = 4, indicating that R = 2.

Outlines

00:00

📐 Introduction to Polar Coordinates

This paragraph introduces polar coordinates, explaining that they are written in the form (R, θ). It defines R as the distance from the pole (origin) and θ as the angle formed by the polar axis. The content covers plotting points with polar coordinates and highlights the difference from Cartesian coordinates. Examples include plotting points with both positive and negative radii and different angles, showing how polar coordinates describe points in two-dimensional space.

05:02

🔄 Multiple Representations of Points in Polar Coordinates

The paragraph discusses how the same point can be represented in different ways using polar coordinates. It provides examples of converting points with given polar coordinates to other forms with different ranges for θ and R, including negative angles and radii. The explanation includes step-by-step plotting of points and converting them while maintaining the same location in the polar coordinate system.

10:04

🔄 Converting Between Polar and Rectangular Coordinates

This section explains the relationship between polar coordinates (R, θ) and rectangular coordinates (X, Y). It details the formulas for converting between the two systems, including R = √(x² + y²), θ = tan⁻¹(y/x), x = R cos(θ), and y = R sin(θ). The paragraph also includes examples of converting specific points from polar to rectangular coordinates, demonstrating the process through calculations.

15:07

✏️ Converting Equations from Rectangular to Polar Coordinates

The paragraph focuses on converting equations from rectangular to polar coordinates. It uses specific examples to illustrate how to replace x and y with R cos(θ) and R sin(θ), respectively, and simplifies the equations accordingly. The discussion includes handling complex equations and solving for R when necessary, highlighting the differences in manipulation between rectangular and polar forms.

20:08

🔄 Converting Equations from Polar to Rectangular Coordinates

This paragraph explains the process of converting equations from polar to rectangular coordinates. It provides examples where polar equations are multiplied by R to facilitate substitution of R² with x² + y² and R sin(θ) with y. The section also discusses completing the square to convert polar equations into standard rectangular forms, such as circles, and identifies the center and radius of the resulting equations.

🎬 Conclusion and Next Steps

The final paragraph summarizes the key points covered in the video about polar coordinates and their conversion to and from rectangular coordinates. It mentions that the next video will focus on graphing in polar coordinates, building on the foundational knowledge provided in this lesson.

Mindmap

Keywords

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system where each point on a plane is determined by a distance from a reference point, known as the pole, and an angle from a reference direction. In the video, the concept is introduced as an alternative to the Cartesian coordinate system, with points represented as (R, θ), where R is the radial distance and θ is the angle. The script explains how to plot points using polar coordinates and how they differ from the rectangular (Cartesian) coordinates that viewers are more familiar with.

💡Radius (R)

The radius, denoted as 'R' in polar coordinates, is the distance from the pole (origin) to the point P in the plane. The script clarifies that R is the shortest distance between the pole and the point, and it is used in conjunction with the angle θ to pinpoint the location of a point in the polar coordinate system. For instance, in the example given, 'R is equal to 2' indicates that the point is two units away from the origin along the line that makes an angle θ with the positive x-axis.

💡Theta (θ)

Theta, represented by the symbol 'θ', is the angle in a polar coordinate system that is formed between the polar axis (typically the positive x-axis) and the line segment connecting the pole to the point P. The script explains that θ can be measured in degrees or radians, and it is used to determine the direction from the pole to the point. An example from the script is 'theta is 7 PI over 6', which specifies the angle at which the point is located relative to the positive x-axis.

💡Cartesian Coordinates

Cartesian coordinates, also known as rectangular coordinates, are a system where each point on a plane is defined by an ordered pair (X, Y), indicating how far the point is from two perpendicular axes, typically the x-axis and y-axis. The video script contrasts polar coordinates with Cartesian coordinates to help viewers understand the differences and similarities between the two systems. The script also provides formulas for converting between these two coordinate systems.

💡Conversion Formulas

Conversion formulas are mathematical equations that allow the translation between polar and Cartesian coordinate systems. The script outlines the formulas x = R * cos(θ) and y = R * sin(θ) for converting from polar to Cartesian coordinates. Conversely, to convert from Cartesian to polar, the script mentions R squared equals X squared plus Y squared, and tan(θ) equals Y over X, provided X is not zero. These formulas are essential for understanding the relationship between the two coordinate systems.

💡Right Triangle

A right triangle is a triangle that has one angle that is a right angle (90 degrees). In the context of the video, the right triangle is formed by the x-axis, the line segment from the pole to point P, and the vertical line from point P to the x-axis. The script uses the properties of a right triangle to explain the trigonometric ratios that relate the Cartesian coordinates (X, Y) to the polar coordinates (R, θ), such as cos(θ) = X / R and sin(θ) = Y / R.

💡Tangent (tan)

Tangent is a trigonometric function that in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. In the script, tangent is used to find the angle θ when converting from Cartesian to polar coordinates, with the formula tan(θ) = Y / X. The script also notes that this method is valid as long as X is not zero, to avoid undefined tangent values.

💡Degenerate Case

A degenerate case in the context of polar coordinates refers to a situation where the radius R is zero, which corresponds to the point being at the pole itself. The script briefly mentions this when discussing the conversion formulas, noting that if R equals 0, it does not affect the graph or the information derived from it, but it is a special case to consider.

💡Graphing

Graphing in the video script refers to the process of plotting points and curves based on their coordinates. The script discusses how to graph points using polar coordinates and how to visualize the relationship between polar and Cartesian coordinate systems. It also hints at future content where graphing in polar coordinates will be explored in more depth.

💡Equation Manipulation

Equation manipulation involves altering the form of an equation to make it more useful or to reveal certain properties. In the script, this concept is demonstrated when converting equations from rectangular to polar coordinates, such as multiplying through by R to eliminate terms like sine theta or cosine theta without an accompanying R. The script shows how this can simplify the process of graphing and understanding the geometric shapes represented by the equations.

💡Secant and Cosecant

Secant and cosecant are trigonometric functions that are reciprocals of the cosine and sine functions, respectively. The script briefly introduces these functions when rewriting an equation in polar coordinates, using the formula 1/4 secant squared theta + cosecant squared theta to express the relationship between R and the trigonometric functions of theta.

Highlights

Introduction to polar coordinates and their representation in the form R, comma theta.

Explanation of R as the distance from the pole to a point P and theta as the angle formed with the polar axis.

Demonstration of plotting points with given polar coordinates, including handling negative radii.

Illustration of the non-uniqueness of polar coordinates and the possibility of multiple representations for a single point.

Conversion formulas between polar and rectangular coordinates, including the use of trigonometric ratios.

Method to convert rectangular coordinates to polar coordinates using the equations R^2 = x^2 + y^2 and tan(theta) = y/x.

Example of converting specific polar coordinates to rectangular coordinates and vice versa.

Discussion on the relationship between the angle theta and its position relative to the quadrants in polar coordinates.

Explanation of how to handle negative angles in polar coordinates by sweeping out angles in a clockwise direction.

Use of graphical illustrations to demonstrate the conversion process between coordinate systems.

Clarification on the conditions under which the conversion formulas are applicable, such as avoiding division by zero.

Application of polar coordinates in simplifying equations and understanding their geometric representations.

Transformation of equations from rectangular to polar coordinates by substituting x and y with R*cos(theta) and R*sin(theta).

Example of solving for R in a polar equation by isolating terms and using trigonometric identities.

Identification of degenerate cases in polar coordinates where R equals zero and their implications.

Transition from polar to rectangular coordinates in equations by multiplying through by R and substituting with x and y.

Completion of the square technique applied to convert a polar equation into the standard form of a circle in rectangular coordinates.

Conclusion summarizing the importance of understanding polar coordinates and their applications in mathematics.

Transcripts

Browse More Related Video

Ch. 8.1 Polar Coordinates

Calculus 2: Polar Coordinates (Video #30) | Math with Professor V

Polar Coordinates Basic Introduction, Conversion to Rectangular, How to Plot Points, Negative R Valu

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Polar Coordinates and Polar Graphs

AP Calculus BC Lesson 9.7

Related Tags

Polar Coordinates Cartesian System Mathematics Educational Video Graphing Coordinate Conversion Trigonometry Geometry Math Tutorial Polar Graphing