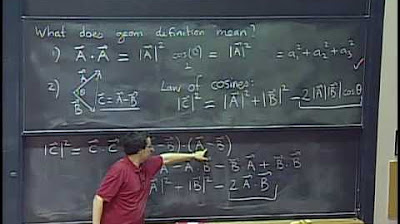Ch. 9.2 The Dot Product
TLDRThis educational video script delves into the concept of the dot product, a fundamental operation in vector mathematics. It explains how the dot product multiplies two vectors to yield a scalar, contrasting it with the multiplication of real numbers. The script covers the formula for the dot product, its properties, and geometric interpretation involving angles between vectors. It further explores applications, such as determining orthogonality, calculating scalar projections, and modeling real-world scenarios like projectile motion and forces acting on a skier. The script concludes with a discussion on work, relating it to the dot product and its geometric significance.
Takeaways
- 📚 The dot product is a method of multiplying two vectors to obtain a scalar value, not another vector.
- 🔢 The dot product of two vectors in R2 is calculated by multiplying corresponding components and summing the results (a1*b1 + a2*b2).
- 📏 The notation for the dot product is represented as 'a dot b', and it's a standard definition in vector multiplication.
- 🔄 The dot product is commutative, meaning the order of vectors does not affect the result (a dot b = b dot a).
- ⚖️ The dot product has properties similar to real number multiplication, including distribution over vector addition.
- 📉 The dot product of a vector with itself gives the square of its norm, which is always non-negative and zero only for the zero vector.
- 📐 The geometric interpretation of the dot product is the product of the magnitudes of the two vectors and the cosine of the angle between them.
- 🛑 The dot product equals zero if and only if the vectors are orthogonal (perpendicular) to each other.
- 📈 The dot product can be used to find the angle between two vectors by using the inverse cosine of the dot product divided by the product of their magnitudes.
- 🏂 The concept of orthogonality and projections is crucial in understanding and modeling real-world scenarios such as the motion of a skier on a slope.
- 🔨 Work in physics is calculated as the dot product of the force vector and the displacement vector, highlighting the importance of direction in the work done.
Q & A
What is the dot product and how does it differ from the multiplication of real numbers?
-The dot product is a form of vector multiplication that results in a scalar value or real number, unlike the multiplication of real numbers which results in another real number. It involves multiplying corresponding components of two vectors and then summing those products.
How is the dot product calculated for two vectors in R2?
-In R2, where each vector has two elements, the dot product is calculated by multiplying the first elements of each vector (a1*b1) and the second elements (a2*b2), and then adding the two products together.
What is the notation used for the dot product of two vectors?
-The notation for the dot product of two vectors a and b is represented as 'a dot b' or written as 'a·b'.
What are some properties of the dot product?
-Some properties of the dot product include commutativity (a·b = b·a), distributivity over vector addition ((a + b)·c = a·c + b·c), and scalar multiplication (λ(a·b) = (λa)·b = a·(λb)).
How is the norm squared of a vector related to the dot product?
-The norm squared of a vector is the dot product of the vector with itself. It is always positive or zero, and equals zero if and only if the vector is the zero vector.
Can you explain the geometric definition of the dot product?
-The geometric definition of the dot product is the product of the magnitudes (lengths) of two vectors and the cosine of the angle between them. It measures how much two vectors point in the same direction.
How can the dot product be used to find the angle between two vectors?
-The angle between two vectors can be found by taking the arccosine (inverse cosine) of the dot product divided by the product of the magnitudes of the two vectors.
What is the concept of orthogonality in relation to the dot product?
-Orthogonality refers to the condition where two vectors are perpendicular to each other, forming a 90-degree angle. If the dot product of two vectors is zero, it indicates that the vectors are orthogonal.
What is the scalar projection of one vector onto another and how is it calculated?
-The scalar projection of one vector onto another is the component of the first vector that is in the direction of the second vector. It is calculated as the dot product of the two vectors divided by the magnitude of the vector being projected onto.
How can the concepts of dot product and scalar projection be applied to model real-world scenarios like projectile motion?
-In projectile motion, the initial velocity can be broken down into horizontal and vertical components using scalar projection. These components can be analyzed separately to understand the motion in each direction, considering forces like gravity and the initial velocity.
What is the significance of breaking a vector into orthogonal components in physics?
-Breaking a vector into orthogonal components allows for the separate analysis of forces or motions in different directions. This is particularly useful in physics for understanding phenomena like projectile motion, where the horizontal motion is independent of the vertical motion influenced by gravity.
Can you provide an example of how to calculate the acceleration of a skier on a sloped mountain using the concepts from the script?
-To calculate the acceleration of a skier on a sloped mountain, you would use the force of gravity (weight of the skier), the slope angle, and trigonometry. By creating a right triangle with the slope angle and using the sine function, you can find the component of the gravitational force acting down the slope, which corresponds to the acceleration of the skier.
How is the dot product used in the context of work done by a force?
-In the context of work, the dot product is used to calculate the work done by a force in a particular direction. Work is the scalar product of the force vector and the displacement vector in the direction of the force.
Outlines
📚 Introduction to the Dot Product
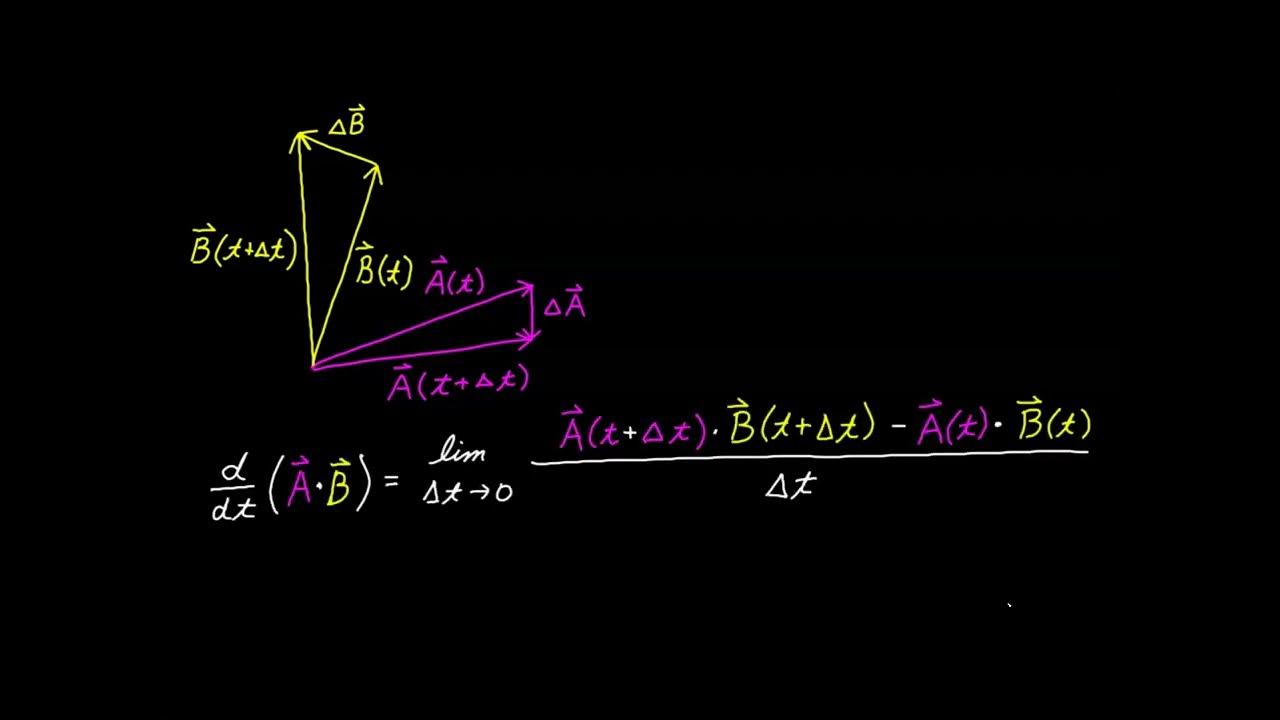
The instructor begins by introducing the concept of the dot product, a method of multiplying two vectors to obtain a scalar value, as opposed to the multiplication of real numbers which yields another real number. The dot product involves multiplying corresponding components of two vectors and summing the results. The lecture clarifies that in R2, where vectors have only two elements, the dot product is calculated by multiplying the first elements of each vector and adding the product of the second elements. The notation for the dot product is represented as 'a dot b'. The instructor also emphasizes the importance of understanding the standard definition of the dot product, which involves memorizing the component-wise multiplication and summing process, and provides an example using vectors a = (2, 3) and b = (-1, 2), resulting in a dot product of 4.
🔍 Properties and Geometric Interpretation of the Dot Product
The video script delves into the properties of the dot product, highlighting its commutative nature, its distributive property over vector addition, and its behavior with respect to scalar multiplication. The instructor explains that the dot product of a vector with itself yields the vector's norm squared, which is always non-negative and equals zero if and only if the vector is the zero vector. The geometric interpretation of the dot product is introduced as the product of the magnitudes of the two vectors and the cosine of the angle between them, which provides insight into the directional relationship between vectors. The instructor illustrates that the dot product can be used to determine the angle between two vectors using the inverse cosine function and discusses the concept of orthogonality, where vectors are perpendicular and their dot product is zero.
📐 Scalar Projection and Orthogonality
The script continues with an exploration of scalar projection, which is the concept of projecting one vector onto another. The instructor describes the process of projecting vector b onto vector a as finding the component of b that lies along a, calculated as the dot product of a and b divided by the magnitude of a, and then multiplied by a. This projection is a scalar multiple of vector a and represents the shadow cast by vector b when light is shone perpendicularly onto vector a. The concept of orthogonality is revisited, emphasizing that if the dot product of two vectors is zero, they are orthogonal to each other. The instructor also introduces the formula for the projection of b onto a, which is a critical tool for understanding the relationship between vectors.
🚀 Decomposing Vectors into Orthogonal Components
The instructor demonstrates how to decompose a vector into its orthogonal components, using the projection concept to break down vector b into a component parallel to vector a and another component orthogonal to a. This decomposition is visualized as creating a parallelogram where the diagonal represents vector b, and the other two sides represent the orthogonal components. The script explains that by subtracting the projection of b onto a from vector b, the orthogonal component can be found. This process is essential for understanding motion, as it allows for the separation of a vector into parts that move in different directions, such as the horizontal and vertical components of projectile motion.
🎯 Applications in Physics: Modeling Motion and Forces
The script applies the concepts of vector decomposition to real-world scenarios, such as the motion of a projectile under the influence of gravity and the forces acting on a skier descending a slope. The instructor uses the example of a skier to illustrate how the force of gravity can be decomposed into components parallel and perpendicular to the slope of the mountain, affecting the skier's acceleration. The video script also introduces the concept of work, defined as the dot product of force and displacement vectors, and explains how the geometric interpretation of the dot product is particularly relevant when the force and displacement are not in the same direction.
📘 Calculation of Acceleration and Work
In the final paragraph, the instructor provides a detailed example of calculating the acceleration of a skier on a mountain with a 15-degree slope, considering the force of gravity and the skier's weight. The script guides through the process of creating reference triangles to apply trigonometric functions and solve for the magnitude of the acceleration vector. The skier's acceleration is found to be 41.41 feet per second squared. The concept of work is also discussed, with the script explaining how work is calculated as the scalar product of force and displacement vectors, particularly when there is an angle between them, and the geometric interpretation of the dot product is emphasized for this purpose.
Mindmap
Keywords
💡Dot Product
💡Scalar Value
💡Vector Multiplication
💡Component-wise Multiplication
💡Norm Squared
💡Orthogonality
💡Scalar Projection
💡Vector Projection
💡Component of a Vector
💡Geometric Definition
💡Work (Physics)
Highlights
Introduction to the dot product and its distinction from real number multiplication.
Explanation of the dot product resulting in a scalar value rather than another vector.
Definition and computation of the dot product through component-wise multiplication and addition.
Notation of the dot product and its standard form.
Example calculation of the dot product for vectors 2 3 and -1 2.
Properties of the dot product, including commutativity and its behavior with respect to vector addition.
Illustration of the dot product's distributive property across vector addition.
Clarification of scalar multiplication's effect on the dot product.
Discussion on the norm squared of a vector and its relationship to the dot product.
Proof that the norm squared is equivalent to the dot product of a vector with itself.
Geometric interpretation of the dot product as the product of magnitudes and cosine of the angle between vectors.
Use of the dot product to measure the directional similarity between two vectors.
Method to find the angle between two vectors using the dot product.
Concept of orthogonality and its connection to the dot product being zero.
Introduction to scalar projection and its formula.
Geometric representation of scalar projection as the shadow cast by one vector onto another.
Explanation of how to break down a vector into its orthogonal components.
Application of vector decomposition in physics, specifically in modeling projectile motion.
Example of calculating skier's acceleration using vector components and trigonometry.
Transition to the concept of work, defined as the dot product of force and direction vectors.
Importance of the geometric definition of the dot product in calculating work.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: