How to Solve By Completing the Square (NancyPi)

NancyPi

28 Aug 201817:33

EducationalLearning

32 Likes 10 Comments

TLDRIn this instructional video, Nancy teaches the method of solving quadratic equations by completing the square. She explains that while this method is not always the most efficient, it is essential to understand for specific cases. Nancy covers three scenarios: equations starting with a positive x^2, those with a coefficient greater than 1 in front of x^2, and equations with a negative coefficient. She emphasizes the importance of adding the correct number to both sides to form a perfect square and not forgetting the plus and minus when taking the square root to find all solutions. The video aims to clarify common mistakes and misconceptions about completing the square.

Takeaways

📚 Completing the square is a method to solve quadratic equations by transforming them into a perfect square form.
🔍 It's not always the easiest method; factoring or the quadratic formula are often more straightforward.
📉 The process involves moving constants to one side and manipulating the equation to form a perfect square on the other side.
🔑 The key step is adding a specific number, derived from the coefficient of the middle term, to both sides of the equation to create a perfect square.
⚠️ Remember that the sign of the constant term changes when moved to the other side of the equation.
🔢 The number to add is found by taking half of the middle coefficient, squaring it, and adding it to both sides.
📐 After creating the perfect square, the equation can be solved by taking the square root of both sides.
💡 When taking the square root, always consider both the positive and negative solutions to avoid missing potential answers.
📉 Completing the square can become complex with coefficients greater than 1 or negative coefficients in front of x^2.
🚫 Completing the square is not possible if there is no x term in the equation, which requires alternative methods like factoring or the quadratic formula.
👍 The video script emphasizes the importance of understanding the method, even if it's not always the preferred approach to solving quadratic equations.

Q & A

What is the method of 'completing the square' used for?
-The method of completing the square is used to solve quadratic equations by transforming them into a perfect square form, making it easier to find the solutions.
Why might completing the square not be the best method for solving a quadratic equation?
-Completing the square is not usually the best method because it can be more complex and time-consuming compared to factoring or using the quadratic formula, which can be applied to all quadratic equations.
What are the three cases of quadratic equations discussed in the script for completing the square?
-The three cases are: 1) when the highest term is a positive x^2, 2) when there is a coefficient greater than 1 in front of the x^2, and 3) when there is a negative coefficient in front of the x^2.
Why can't you complete the square if there is no middle x term in the equation?
-If there is no middle x term, there is no coefficient to use when adding a number to both sides of the equation, which is a necessary step in the process of completing the square.
What is the first step in solving a quadratic equation by completing the square?
-The first step is to move the constant term to the right side of the equation by adding or subtracting it from both sides.
How do you determine the number to add to both sides of the equation when completing the square?
-You determine the number by taking the coefficient of the middle x term, dividing it by 2, and then squaring the result.
What is the purpose of adding a number to both sides of the equation after moving the constant term?
-The purpose is to create a perfect square trinomial on the left side of the equation, which allows you to express the equation in the form of a squared binomial.
Why is it important to remember to include both the positive and negative square roots when solving the equation after completing the square?
-It is important because each square root represents a potential solution to the equation, and omitting one would result in missing a solution.
How do you handle a quadratic equation with a coefficient greater than 1 in front of the x^2 when completing the square?
-You divide every term in the equation, including the constant term, by the coefficient of x^2 to simplify the equation before proceeding with the usual steps of completing the square.
What should you do if you encounter a quadratic equation with a negative coefficient in front of the x^2?
-You should first move the constant term to the right side and then divide every term by -1 to eliminate the negative sign in front of the x^2 before completing the square.

Outlines

00:00

📚 Introduction to Completing the Square

Nancy introduces the concept of completing the square, explaining it as a method to rearrange an equation into a perfect square form. She clarifies that while this method is not the most efficient, it is essential to understand when required. Nancy outlines three common scenarios for completing the square: equations starting with a positive x^2, those with a coefficient greater than 1 in front of x^2, and those with a negative coefficient in front of x^2. She emphasizes that equations without an x term cannot be solved using this method. The first step in solving these equations is always to move the constant term to the right side of the equation.

05:01

🔍 Steps for Completing the Square with Positive x^2

Nancy demonstrates the process of completing the square for equations starting with a positive x^2. She explains that after moving the constant to the right side, the next step is to add a specific number to both sides of the equation, which is derived from the coefficient of the middle term (x) divided by 2 and then squared. This addition transforms the left side into a perfect square trinomial, allowing the equation to be rewritten as a squared binomial equal to a constant. Nancy then shows how to solve for x by taking the square root of both sides, resulting in two potential solutions due to the plus and minus nature of square roots.

10:03

📘 Completing the Square with Coefficients Other Than 1

In this section, Nancy addresses equations with coefficients greater than 1 in front of x^2. She illustrates the process by first moving the constant to the right side and then dividing every term in the equation by the coefficient of x^2 to simplify the equation. After this, the same process of adding a number, derived from the new coefficient of the middle term divided by 2 and squared, is applied to both sides. This results in a perfect square on the left side, which can then be solved by taking the square root of both sides, leading to two solutions.

15:05

📙 Completing the Square with Negative Coefficients and Common Pitfalls

Nancy discusses the process for equations starting with a negative x^2, explaining the initial step of moving the constant to the right side and then dividing every term by -1 to eliminate the negative sign in front of x^2. She reiterates the steps of adding a number to both sides, derived from the coefficient of the middle term, to form a perfect square. The summary also highlights common mistakes made when completing the square, such as forgetting to include both the positive and negative solutions after taking the square root and attempting to complete the square when there is no x term present in the equation.

👍 Conclusion and Encouragement

In the concluding paragraph, Nancy summarizes the importance of understanding the method of completing the square, even if it's not always the preferred method for solving quadratic equations. She humorously suggests that while viewers may not find the process fascinating, they can appreciate the explanation and show their support by liking the video.

Mindmap

Keywords

💡Completing the square

Completing the square is a mathematical method used to solve quadratic equations by transforming them into a perfect square trinomial plus or minus a constant. In the video, it is the primary technique being explained for solving equations of the form x^2 + bx + c = d. The process involves moving the constant term to one side, adjusting the equation to have a perfect square on the other side, and then solving for the variable by taking the square root of both sides.

💡Quadratic equation

A quadratic equation is a polynomial equation of degree two, typically in the form ax^2 + bx + c = 0, where a, b, and c are constants. In the context of the video, quadratic equations are the focus, and the script discusses how to solve them using the method of completing the square, as well as mentioning alternative methods such as factoring and the quadratic formula.

💡Coefficient

In mathematics, a coefficient is a numerical factor that multiplies a variable in an algebraic expression. In the video, the term is used to describe the numbers that multiply the x terms in the quadratic equations, such as '2x^2' where 2 is the coefficient of x^2. The script explains how to handle different coefficients when completing the square.

💡Perfect square trinomial

A perfect square trinomial is a special type of quadratic expression that can be factored into the square of a binomial. In the video, the process of completing the square aims to transform the quadratic equation into this form, such as (x + b/2)^2, which simplifies the process of finding the solution for x.

💡Middle term

The middle term in a quadratic equation refers to the linear term involving 'x', such as 'bx' in the equation ax^2 + bx + c. The video script explains how the coefficient of this middle term is used to determine the number to add to both sides of the equation when completing the square.

💡Square root

The square root operation is used to find a number that, when multiplied by itself, gives the original number. In the video, taking the square root is a step in the process of solving the equation after completing the square, as it allows for the isolation of the variable x and finding its possible values.

💡Solving equations

Solving equations involves finding the values of the variables that make the equation true. The video script provides a detailed guide on how to solve quadratic equations using the method of completing the square, which is one of several methods for finding the solutions to such equations.

💡Factoring

Factoring is a method of breaking down a polynomial into a product of its factors. In the script, factoring is mentioned as an alternative method for solving quadratic equations when possible, suggesting that it can be simpler or more straightforward than completing the square in some cases.

💡Quadratic formula

The quadratic formula is a standard algebraic method for solving quadratic equations, represented as x = (-b ± √(b^2 - 4ac)) / (2a). The video script mentions it as a reliable method that can always be used to solve quadratic equations, regardless of their form.

💡Constant term

In an algebraic expression, the constant term is the term that does not contain any variables. In the context of the video, the constant term is initially moved to one side of the equation to facilitate the process of completing the square and is later involved in the formation of the perfect square trinomial.

💡Balancing the equation

Balancing an equation means ensuring that both sides of the equation remain equal after performing operations on one side. The video emphasizes the importance of adding the same value to both sides when completing the square to maintain the balance and integrity of the equation.

Highlights

Introduction of completing the square as a method to solve quadratic equations.

Explanation of when completing the square is not the most efficient method compared to factoring or using the quadratic formula.

Demonstration of the process to complete the square for equations starting with a positive x^2 term.

Step-by-step guide on moving constants to the right side of the equation in the process of completing the square.

Clarification on the importance of sign flipping when moving constants to the other side of the equation.

Instruction on how to determine the number to add to both sides of the equation for completing the square.

Example of completing the square for an equation with a middle term coefficient of 6.

Transformation of the equation into a perfect square trinomial and its subsequent simplification.

Use of square roots to solve the equation after completing the square.

Emphasis on the necessity of considering both positive and negative square roots when solving.

Presentation of two solutions derived from completing the square for a given example.

Approach to complete the square for equations with a coefficient greater than 1 in front of x^2.

Technique of dividing every term by the coefficient of x^2 to simplify the equation for completing the square.

Handling of fractions when adding a number to both sides in the process of completing the square.

Conversion of the left side of the equation into a perfect square and solving it.

Strategy for dealing with equations starting with a negative x^2 term in the process of completing the square.

Common mistakes people make when completing the square, such as forgetting to include both positive and negative solutions.

Special case where completing the square is not possible due to the absence of an x term.

Conclusion and reminder of the importance of understanding completing the square despite its complexity.

Transcripts

Browse More Related Video

Solve by Completing the Square: Step-by-Step Technique

Using Factoring to Solve Quadratics (Precalculus - College Algebra 18)

How to Solve Quadratic Equations by Factoring (NancyPi)

The Square Root Method in Solving Quadratics (Precalculus - College Algebra 17)

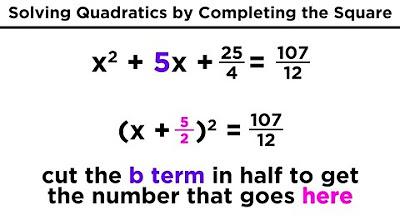
Solving Quadratics by Completing the Square

Solving Quadratic Equations By Completing The Square