How to Solve Quadratic Equations using Three Methods - When Leading Coefficient is Not One

PreMath
1 Jun 201815:42
EducationalLearning
32 Likes 10 Comments

TLDRIn this tutorial, we explore three methods to solve a quadratic equation: using the quadratic formula, factoring, and completing the square. The equation in question has a leading coefficient other than one, making the solutions slightly more complex. Each method is explained step-by-step, from setting up the equation and simplifying terms to isolating the variable and verifying solutions. By the end, viewers will have a comprehensive understanding of how to tackle quadratic equations using different techniques. Subscribe for more educational content.

Takeaways
  • 📚 The video is a tutorial on solving a quadratic equation using three different methods.
  • 🔢 The quadratic formula method is demonstrated first, with the coefficients a=10, b=13, and c=-3.
  • 📝 The quadratic formula is applied to find the solutions x = 1/5 and x = -3/2.
  • 🔍 The factoring method is introduced as the second approach, emphasizing the leading coefficient of 10.
  • 📐 The process of factoring involves finding two numbers that multiply to 30 and add to 13, resulting in the factors (5x - 1) and (2x + 3).
  • 🧩 The solutions from factoring are the same as from the quadratic formula: x = 1/5 and x = -3/2.
  • 📈 The third method, completing the square, is explained step by step, starting with isolating the x terms.
  • 📉 The leading coefficient is normalized to 1 by dividing the entire equation by 10.
  • 🔄 The process involves adjusting the equation to a perfect square trinomial and solving for x.
  • 🎯 The completing the square method also yields the solutions x = 1/5 and x = -3/2.
  • 👍 The video concludes by summarizing the solutions and encouraging viewers to subscribe for more content.
Q & A

  • What are the three methods discussed in the video to solve a quadratic equation?

    -The video discusses solving a quadratic equation using the quadratic formula, factoring, and completing the square.

  • What is the leading coefficient of the quadratic equation in the video?

    -The leading coefficient of the quadratic equation in the video is 10, which is other than one.

  • What are the values of coefficients a, b, and c in the quadratic formula used in the video?

    -In the quadratic formula, the values used are a = 10, b = 13, and c = -3.

  • How does the video simplify the quadratic formula to find the solutions for x?

    -The video simplifies the quadratic formula by substituting the values of a, b, and c, and then solving for x by adding and subtracting the square root of the discriminant (b^2 - 4ac) divided by 2a.

  • What are the two solutions for x obtained using the quadratic formula in the video?

    -The two solutions for x obtained using the quadratic formula are x = 1/5 and x = -3/2.

  • How does the video suggest finding factors for the quadratic equation when the leading coefficient is not one?

    -The video suggests multiplying the constant term by the leading coefficient and finding factors of the product that add up to the middle coefficient, then adjusting the equation accordingly.

  • What is the process of factoring the quadratic equation as described in the video?

    -The process involves multiplying the constant term by the leading coefficient, finding factors of the product that add up to the middle coefficient, and then using the greatest common factor to simplify the equation into two binomials set equal to zero.

  • How does the video solve the quadratic equation by completing the square?

    -The video first ensures the x terms are on one side and the constant on the other. It then adjusts the equation so the coefficient of x^2 is 1, and adds the square of half the coefficient of x to both sides, resulting in a perfect square trinomial. The square root of both sides gives the solutions.

  • What is the discriminant in the quadratic formula, and what does it represent?

    -The discriminant in the quadratic formula is the expression under the square root, b^2 - 4ac. It represents the part of the formula that determines the nature of the roots (real and distinct, real and equal, or complex).

  • How does the video ensure the leading coefficient is 1 when completing the square?

    -The video divides all terms of the equation by the leading coefficient to make it 1, which simplifies the process of completing the square.

  • What is the final solution set for the quadratic equation as presented in the video?

    -The final solution set for the quadratic equation is x = -3/2 and x = 1/5.

Outlines
00:00
📚 Introduction to Solving Quadratic Equations

This paragraph introduces a tutorial on solving a given quadratic equation using three distinct methods: the quadratic formula, factoring, and completing the square. It emphasizes that the leading coefficient is not one, setting the stage for a more complex problem-solving approach. The speaker begins by applying the quadratic formula with specific coefficients a, b, and c, demonstrating the process of finding the roots of the equation.

05:00
🔍 Detailed Application of the Quadratic Formula

The speaker provides a step-by-step walkthrough of using the quadratic formula to solve the equation. Coefficients a, b, and c are identified, and the formula is applied to find the values of x. The process involves squaring and adding the terms, simplifying the expression, and eventually finding two solutions for x, which are -3/2 and 1/5. The explanation is thorough, ensuring that viewers understand each step of the calculation.

10:02
🔢 Factoring Technique for Quadratic Equations

In this section, the tutorial shifts to solving the quadratic equation by factoring. The speaker outlines a method to find factors that work with the leading coefficient of 10, using a trick to simplify the process. The equation is manipulated to find common factors and ultimately factored into (5x - 1) and (2x + 3). The solutions to the equation are then found by setting each factor equal to zero, yielding the same solutions as before: -3/2 and 1/5.

15:04
📐 Completing the Square Method

The final method discussed is completing the square. The speaker instructs viewers to isolate the x terms and adjust the equation so that the leading coefficient is 1. The process involves dividing through by the leading coefficient, adding and subtracting terms to create a perfect square trinomial, and then simplifying to find the square root of the constant term. The solutions derived from this method are consistent with the previous methods, confirming the solutions -3/2 and 1/5.

🎉 Conclusion and Call to Action

The tutorial concludes with a summary of the solutions obtained from the three methods and a reminder of the importance of understanding different approaches to solving quadratic equations. The speaker thanks the viewers for watching and encourages them to subscribe to the channel for more educational content.

Mindmap
Keywords
💡Quadratic Equation
A quadratic equation is a polynomial equation of the second degree, typically in the form of ax² + bx + c = 0, where a, b, and c are constants, and x represents an unknown variable. In the video, the quadratic equation is the central theme, with the equation 10x² + 13x - 3 = 0 being solved using different methods.
💡Quadratic Formula
The quadratic formula is a fundamental tool for solving quadratic equations, given by x = (-b ± √(b² - 4ac)) / (2a). In the video, the formula is applied to the provided quadratic equation, demonstrating one of the three methods to find its solutions.
💡Factoring
Factoring is a mathematical method of breaking down a polynomial into a product of its factors. In the context of the video, the quadratic equation is factored into (5x - 1)(2x + 3) = 0, which allows for the solutions to be found by setting each factor equal to zero.
💡Completing the Square
Completing the square is a technique used to solve quadratic equations by transforming them into a perfect square trinomial plus a constant. The video demonstrates this method by manipulating the equation to isolate x and form a perfect square, which is then solved by taking the square root of both sides.
💡Leading Coefficient
The leading coefficient is the coefficient of the term with the highest power of the variable in a polynomial. In the video, it is emphasized that the leading coefficient of the given quadratic equation is 10, which is different from one, and this affects the approach to solving the equation.
💡Greatest Common Factor (GCF)
The GCF of two or more numbers is the largest number that divides all of them without leaving a remainder. In the video, the GCF is used to simplify the factors of the quadratic equation during the factoring process, making it easier to solve.
💡Square Root
A square root of a number is a value that, when multiplied by itself, gives the original number. In the video, square roots are used in the quadratic formula and completing the square methods to find the solutions of the equation.
💡Simplifying
Simplifying refers to the process of making a mathematical expression easier to understand or work with, often by reducing fractions or combining like terms. In the video, the solutions derived from the quadratic formula are simplified to their lowest terms, resulting in 1/5 and -3/2.
💡Solution Set
The solution set of an equation is the set of all possible values of the variable that satisfy the equation. In the video, the solution set for the quadratic equation is found to be -3/2 and 1/5, representing the two values of x that make the original equation true.
💡Coefficient
A coefficient is a numerical factor in a term of an algebraic expression. In the context of the video, coefficients a, b, and c are used in the quadratic formula and are essential in determining the specific form and solution of the quadratic equation.
💡Dividing by Zero
Dividing by zero is a mathematical operation that is undefined, as no number can multiply zero to give a non-zero number. In the video, the process of dividing each term of the equation by the leading coefficient (10 in this case) is mentioned, which is a valid operation as long as the coefficient is not zero.
Highlights

Introduction to solving a quadratic equation with a leading coefficient other than one.

Explanation of three different methods to solve the quadratic equation: quadratic formula, factoring, and completing the square.

Use of the quadratic formula with specific coefficients a=10, b=13, and c=-3.

Step-by-step calculation using the quadratic formula resulting in two potential solutions.

Simplification of the quadratic formula's results to find the solutions x = 1/5 and x = -3/2.

Transition to solving the equation by factoring with a focus on the leading coefficient of 10.

Demonstration of a trick to find factors of the quadratic equation.

Identification of factors 2 and 15 to simplify the equation for factoring.

Process of factoring the quadratic equation to (5x - 1)(2x + 3) = 0.

Solving the factored equation to find the same solutions x = 1/5 and x = -3/2.

Introduction to the completing the square method for solving quadratic equations.

Instructions to isolate the x variable and adjust the equation for a leading coefficient of 1.

Explanation of the process to complete the square by adding and subtracting the square of half the coefficient of x.

Transformation of the equation into a perfect square trinomial and solving for x.

Final solutions obtained by completing the square method, confirming x = 1/5 and x = -3/2.

Conclusion and summary of the solutions for the quadratic equation.

Encouragement to subscribe for more educational content.

Transcripts

Browse More Related Video

Solving Quadratic Equations By Completing The Square

Solve by Completing the Square: Step-by-Step Technique

Proving the Quadratic Formula - Twice (Precalculus - College Algebra 20)

Solving Quadratics by Using the Quadratic Formula

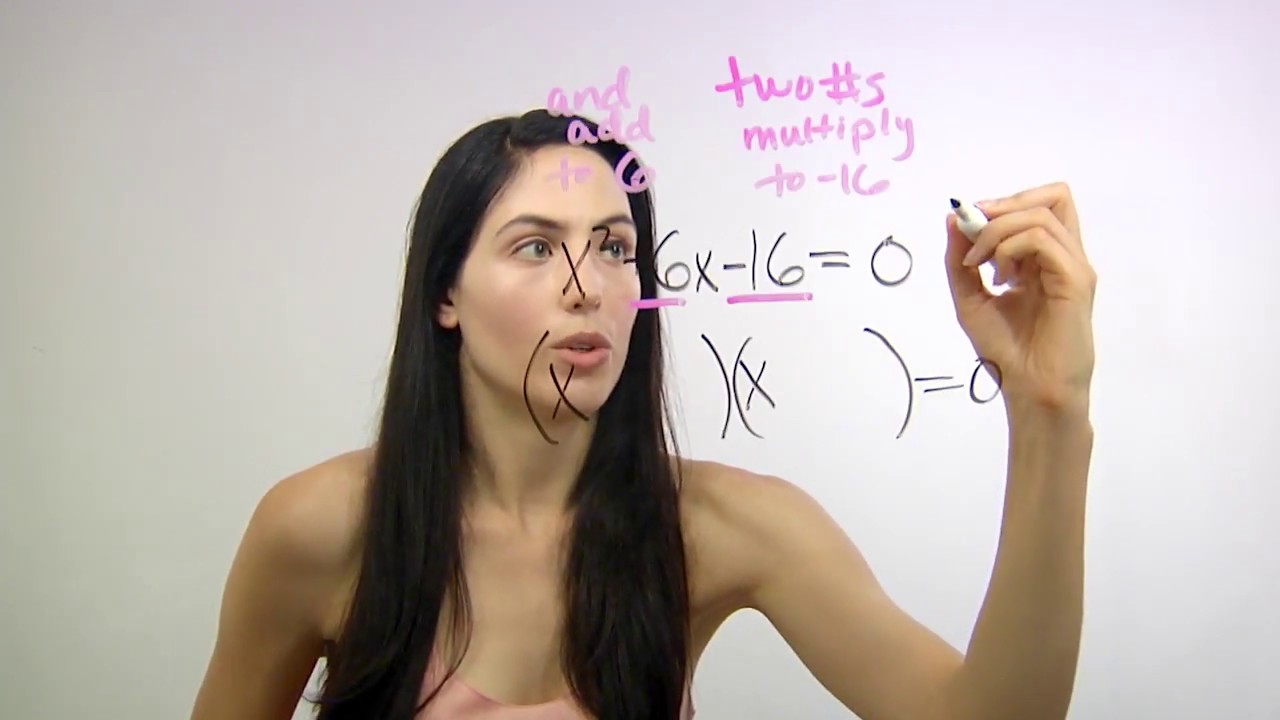
How to Solve Quadratic Equations by Factoring (NancyPi)

Factoring Trinomials - Quick & Simple

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quadratic EquationsMath TutorialSolving TechniquesQuadratic FormulaFactoring MethodCompleting the SquareEducational ContentMathematicsLearning ResourceAlgebraProblem Solving