A proof that e is irrational - Numberphile

Numberphile

24 Jan 202116:29

EducationalLearning

32 Likes 10 Comments

TLDRIn this engaging video, the host explores the intriguing properties of the mathematical constant e, known for its prevalence in physics and mathematics. They define e as the unique number that remains unchanged upon differentiation, demonstrating this with an exponential function. The script then delves into a proof by contradiction, attributed to Joseph Fourier, to establish e's irrationality. Utilizing e's infinite series expansion, the proof shows that e cannot be expressed as a ratio of two integers, thus confirming its irrational nature. The video concludes with a light-hearted reference to a product endorsement, highlighting the host's enthusiasm for educational activities.

Takeaways

📚 The number e is an irrational number, known for its ubiquity in mathematics and physics.
🔍 e is defined as the unique number that, when differentiated, returns itself, which is a distinctive property.
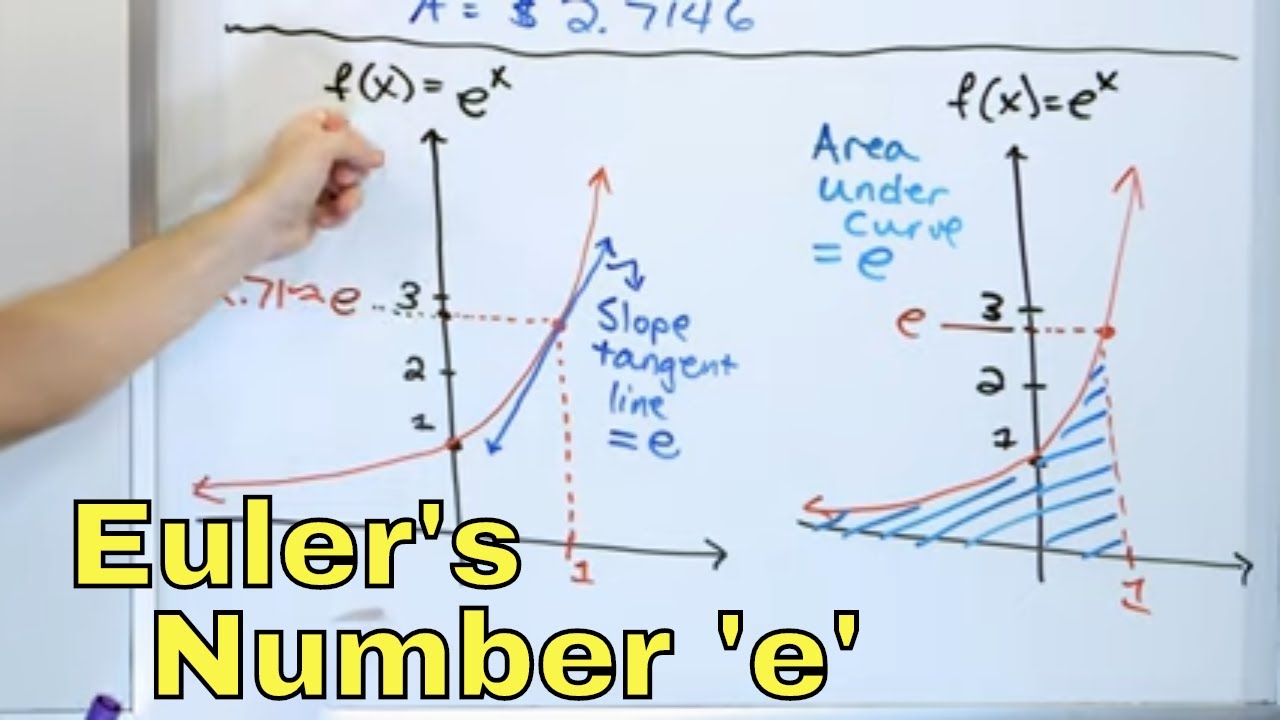
📈 The function e^x is shown graphically to start at 1 and increase rapidly, with its slope at any point being e^x itself.
🌐 e's importance is not just for its mathematical properties but also for its role in natural phenomena and scientific calculations.
🤔 The speaker expresses curiosity about why the property of e being self-similar upon differentiation is so prevalent in nature.
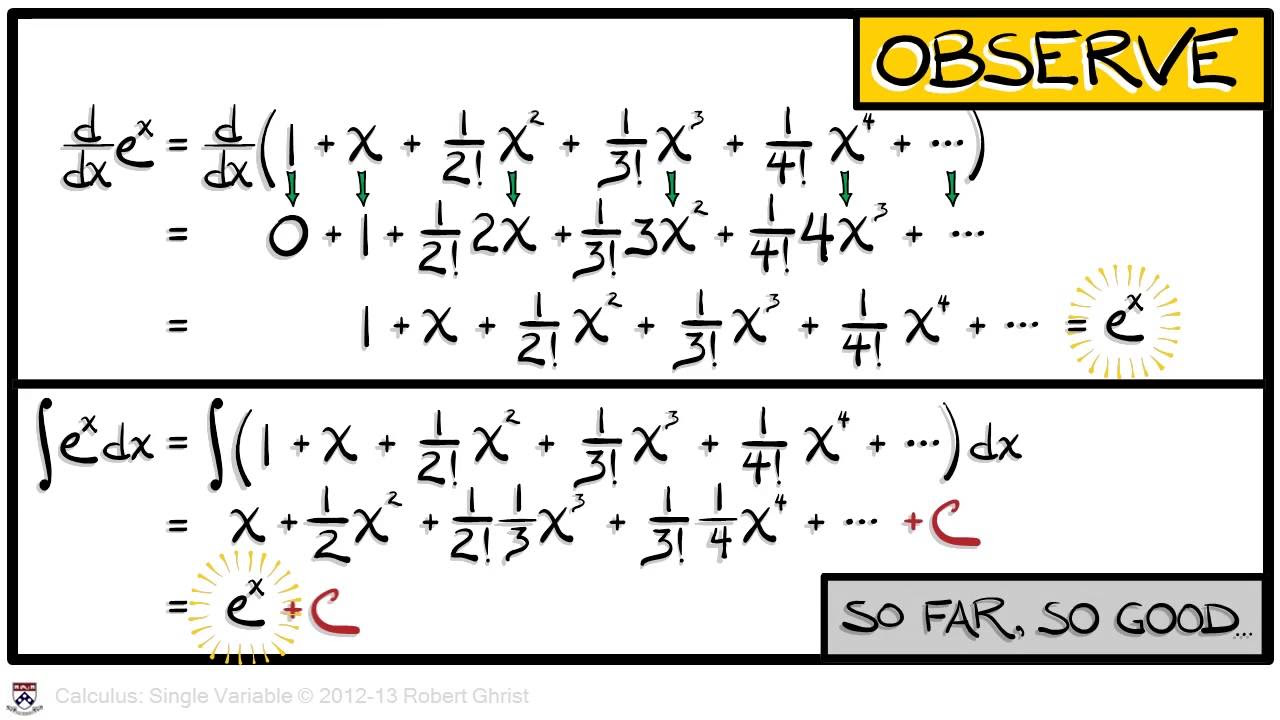
📝 e has an infinite series expansion, which is a common knowledge and taught in schools, represented as 1 plus 1/1! + 1/2! + 1/3! and so on.
🧩 The proof of e being irrational involves assuming the opposite and showing an inconsistency, a method similar to proving the irrationality of the square root of 2.
📉 The script outlines a mathematical process involving multiplying the series expansion of e by q! (q factorial) and simplifying to find a contradiction.
📊 The 'rest' of the series, after multiplying by q!, is shown to be less than a certain fraction, leading to a contradiction if e were rational.
📚 A brief mention of a proof by Gauss is used to establish that the sum of a series involving terms less than 1 converges to 1/(1-x).
🎉 The final conclusion is that since the 'rest' of the series must be an integer but is also less than 1/q, e cannot be rational, thus proving it to be irrational.

Q & A

What is the mathematical constant 'e'?
-The mathematical constant 'e' is approximately 2.718 and is an irrational number that is pervasive in various fields of mathematics and physics. It is unique in that its own derivative is the function itself.
How is 'e' defined in the context of calculus?
-In calculus, 'e' is defined as the base of the natural logarithm, and it is the only number for which the derivative of the function e^x is the function itself, e^x.
What is the significance of 'e' in mathematics and physics?
-The constant 'e' is significant because it appears in many important mathematical formulas and physical laws, such as in the calculation of exponential growth and decay, and in the solution of certain differential equations.
What is an irrational number?
-An irrational number is a real number that cannot be expressed as a ratio of two integers, meaning it cannot be written as a simple fraction.
What is the infinite series expansion of 'e' mentioned in the script?
-The infinite series expansion of 'e' is given by the sum 1 + 1/1! + 1/2! + 1/3! + ..., where 'n!' denotes the factorial of 'n'.
What is the proof that 'e' is irrational based on?
-The proof that 'e' is irrational is based on the assumption that 'e' could be expressed as a ratio of two integers, leading to a contradiction when considering the series expansion of 'e'.
What is the role of the series expansion in proving 'e' is irrational?
-The series expansion of 'e' is used to show that if 'e' were rational, it would lead to an integer being equal to a non-integer value, which is a contradiction, thus proving 'e' must be irrational.
What is the Gauss's proof mentioned in the script?
-Gauss's proof is a method to sum an infinite geometric series where the common ratio is less than 1, showing that the sum converges to 1/(1-x).
How does the script relate the concept of acceleration to the function e^x?
-The script relates acceleration to the function e^x by illustrating that the velocity (first derivative) and acceleration (second derivative) of the function e^x are both equal to the function itself, e^x.
What is the final conclusion of the script regarding the nature of 'e'?
-The final conclusion of the script is that 'e' is proven to be an irrational number, as it cannot be represented as the ratio of two integers.

Outlines

00:00

📚 Introduction to the Irrational Number e

The script begins with an introduction to the mathematical constant e, highlighting its ubiquity in physics and mathematics. The speaker casually refers to e as 'friendly' and humorously contemplates how mathematicians might refer to it in a pub setting. The explanation of e's unique property is given: it is the only number that, when differentiated, yields itself. This is illustrated through the function e^x, which is shown graphically and its derivatives are discussed, emphasizing that all derivatives of e^x are the function itself. The speaker aims to prove e's irrationality, referencing Fourier's proof, and sets the stage for the demonstration.

05:02

🔍 Infinite Series Expansion and Assumption of Rationality

The second paragraph delves into the infinite series expansion of e, a concept familiar to many in mathematics. The speaker proposes a hypothetical scenario where e could be expressed as a ratio of two integers, p and q, which are relatively prime. The script outlines a mathematical approach to multiply an equation representing e's series expansion by q factorial, leading to an equation where the left side is an integer due to the assumption that e = p/q. The right side of the equation is analyzed, showing that it also must be an integer, leading to the conclusion that the 'rest' of the series, denoted as 'r', must also be an integer after simplification.

10:03

📉 Bounding the Remainder and Gauss's Lemma

In this paragraph, the speaker focuses on bounding the remainder 'r' of the series expansion, using an inequality to show that 'r' must be less than a certain value. The script introduces a lemma attributed to Gauss, which is a method for summing a series where the terms are powers of a number less than 1. The lemma is used to establish that the infinite sum of such a series converges to 1/(1-x), where x is replaced by 1/(q+1) in the context of the proof. The remainder 'r' is then bounded by a fraction less than 1, leading to a contradiction since 'r' was previously established to be an integer.

15:04

🎉 Conclusion: e is Irrational

The script concludes with the final step of the proof, showing that the remainder 'r' cannot be an integer because it is less than 1, which contradicts the earlier assertion that 'r' must be an integer. This contradiction implies that the initial assumption that e could be expressed as a ratio of two integers is false, thereby proving that e is an irrational number. The proof is completed with a flourish, and the speaker expresses satisfaction with the demonstration.

🛠️ Sponsor Mention and Educational Activity Promotion

The final paragraph shifts away from the mathematical discussion to acknowledge the episode's sponsor, KiwiCo, which offers subscription boxes for educational and creative activities. The speaker shares a personal experience with a 'tinker crate' and encourages viewers to try KiwiCo with a special offer. The script includes a URL for a discount and ends with a visual of the completed Ballista project, emphasizing the educational and family-friendly nature of KiwiCo's offerings.

Mindmap

Keywords

💡Irrational Number

An irrational number is a real number that cannot be expressed as a ratio of two integers, meaning it cannot be written as a simple fraction. In the video, the main theme revolves around proving that 'e', a fundamental mathematical constant, is indeed irrational. The script uses the historical proof by Joseph Fourier to demonstrate this by assuming the contrary and showing the inconsistency that arises from it.

💡e (Euler's number)

Euler's number, commonly denoted as 'e', is a mathematical constant approximately equal to 2.718. It is the base of the natural logarithm and is omnipresent in various fields of mathematics and physics. The video script discusses 'e' as an important number that is shown to be irrational, playing a central role in the proof presented.

💡Differentiation

Differentiation is a process in calculus that finds the rate at which a quantity changes with respect to another. In the script, the presenter explains that 'e' is unique because its derivative is the number itself, which is a key property used in the proof of its irrationality.

💡Exponential Function

An exponential function is a mathematical function where the variable is in the exponent. The script introduces 'e' as the base of such functions, e^x, and discusses how its properties, such as having the same value for all its derivatives, are crucial to the proof of its irrationality.

💡Series Expansion

A series expansion is a way of expressing a function as an infinite sum of terms. The script mentions the infinite series expansion of 'e', which is 1 plus 1/1! + 1/2! + 1/3! + ..., and uses this expansion in the proof of 'e's irrationality.

💡Factorial

The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. In the script, factorials are used in the series expansion of 'e' and play a significant role in the mathematical manipulations leading to the proof of irrationality.

💡Rational Number

A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where the denominator q is not zero. The script contrasts rational and irrational numbers, aiming to prove that 'e' cannot be expressed as a ratio of two integers.

💡Proof by Contradiction

Proof by contradiction is a common method in mathematics where one assumes the opposite of what they want to prove and then shows that this assumption leads to a contradiction. The script uses this method to demonstrate that 'e' cannot be rational.

💡Gauss's Lemma

Gauss's Lemma, mentioned in the script, is a mathematical result that provides a way to sum an infinite series where the terms are less than 1. The script uses this lemma to bound the remainder of the series expansion of 'e', which is a crucial step in proving its irrationality.

💡Infinite Series

An infinite series is a sequence of numbers that does not have a last term and continues indefinitely. The script discusses the infinite series expansion of 'e' and uses the properties of infinite series in the proof of 'e's irrationality.

💡KiwiCo

KiwiCo is a company that provides subscription-based crates for hands-on learning and creative projects. In the script, it is mentioned as a sponsor of the video, offering educational kits that align with the video's theme of exploration and learning through mathematical concepts.

Highlights

Introduction of the mathematical constant e, its significance in mathematics and physics.

Informal definition of e as a number that differentiates to itself.

Graphical representation of e raised to the power of x and its properties.

Explanation of the slope of the function e^x and its relation to velocity and acceleration.

Differentiation of e^x and its resulting self-similarity across derivatives.

Discussion on the usefulness and the intriguing nature of e's properties.

Introduction of the goal to prove e is an irrational number.

Historical reference to Joseph Fourier and his contribution to the proof of e's irrationality.

Infinite series expansion of e and its common knowledge status.

Assumption for the proof by contradiction that e can be expressed as a fraction.

Multiplication of the series by q factorial and the resulting integer properties.

Identification of the 'rest' term in the series and its significance in the proof.

Application of Gauss's proof to bound the 'rest' term and its implications.

Derivation of the inequality for the 'rest' term and its contradiction with being an integer.

Conclusion that e cannot be a rational number and thus must be irrational.

Sponsorship mention and promotion of KiwiCo's educational crates for children.

Personal anecdote about the enjoyment and educational value of KiwiCo's crates.

Details on how to subscribe and receive a discount on the first KiwiCo crate.

Final remarks on the family activity aspect and the educational potential of KiwiCo's crates.

Transcripts

Browse More Related Video

A Proof That The Square Root of Two Is Irrational

Lec 7: Exam 1 review | MIT 18.01 Single Variable Calculus, Fall 2007

14 - What is Euler's Number 'e', Ln(x) - Natural Log & e^x Functions?

2.2 - Derivatives of Exponential Functions

Calculus Chapter 1 Lecture 2 Exponentials

Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions