Calculus Chapter 1 Lecture 2 Exponentials
TLDRIn this calculus lecture, Professor Greist introduces the exponential function, e^x, and its intriguing properties. He discusses the function's self-derivative nature and its integral counterpart, leading to Euler's formula, which connects the exponential function with trigonometric functions. The definition of e^x is explored through its infinite series representation, and its implications for calculus, including differentiation and integration of polynomials, are highlighted. The lecture also delves into the representation of sine and cosine using the exponential function, offering new insights into their calculus properties without complex proofs.
Takeaways
- 📚 The exponential function, e^x, is the central theme of the lecture, with a focus on its definition and implications.
- 🔍 Professor Greist introduces the concept of exponentiating irrational, imaginary, and complex numbers, and even operators like derivatives.
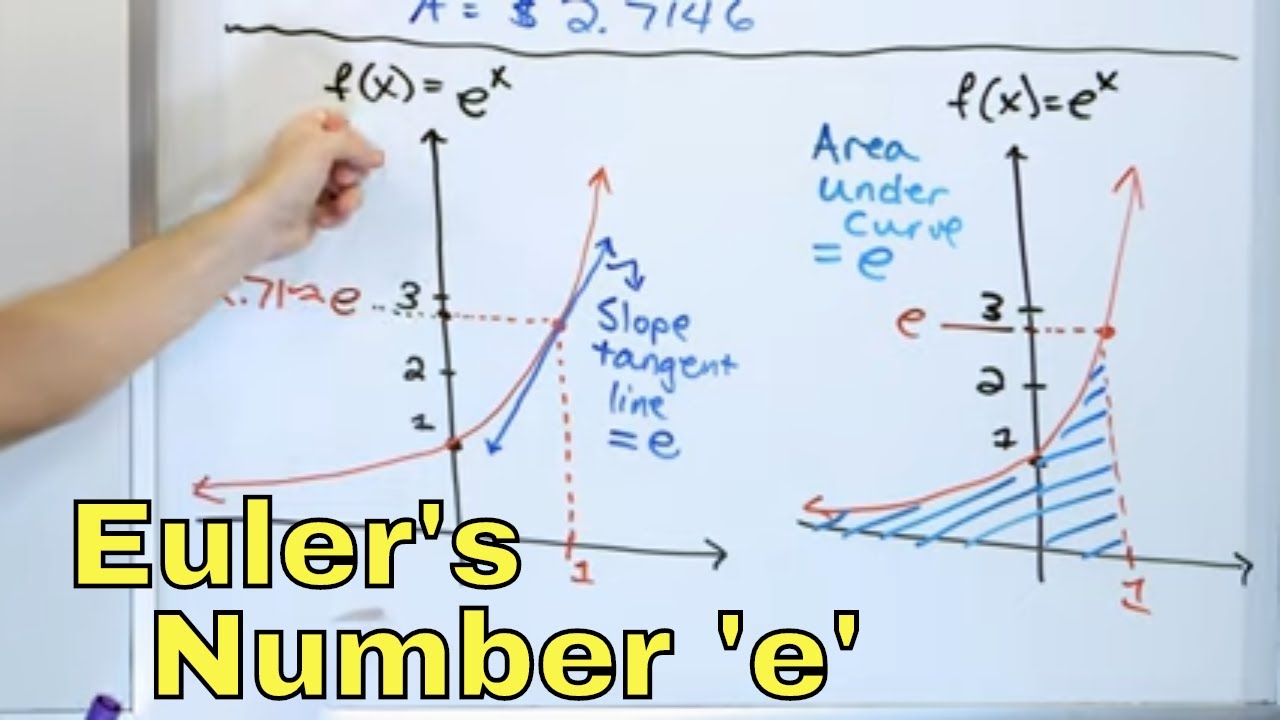
- 🌟 The exponential function is unique in that it is its own derivative and integral, a property not shared by other functions.
- 📈 Euler's formula is highlighted as a key relationship, showing how e^{ix} is connected to trigonometric functions as cos(x) + i*sin(x).
- 📝 The definition of e^x is presented as an infinite series involving factorials, which is a crucial formula to memorize for the course.
- 🔢 The script explains the origin of the numbers in the series expansion of e^x and their significance in calculus.
- 🤔 The concept of dealing with infinite sums is introduced, suggesting that one should treat them like long polynomials for ease of manipulation.
- 📉 Differentiation of e^x is demonstrated using the series definition, showing that it simplifies to the original function, e^x.
- 📈 Integration of e^x is also explored, revealing that it results in the original function plus an arbitrary constant.
- 🌀 Euler's formula is applied to the series definition to derive expressions for sine and cosine in terms of e^{iθ}.
- 📚 The properties of sine and cosine with respect to calculus are revisited, and their derivatives are derived using the series expressions.
- 🔄 The script concludes by encouraging students to review the material and seek comfort in the bonus lecture before moving on to the next topic.
Q & A
What is the main focus of Lecture 2 in the calculus course by Professor Greist?
-The main focus of Lecture 2 is the exponential function, its definition, properties, and its relationship with trigonometric functions through Euler's formula.
What is the algebraic property of the exponential function e^x that is mentioned in the lecture?
-The algebraic property mentioned is that e^x is its own derivative and its own integral up to a constant of integration.
How is the exponential function e^x defined in the lecture?
-The exponential function e^x is defined as the infinite series: e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + ... which continues indefinitely.
What does Euler's formula state regarding the exponential function?
-Euler's formula states that e^(ix) = cos(x) + i*sin(x), intertwining the exponential function with the basic trigonometric functions cosine and sine.
How does the lecture describe the computation of e^x for specific values such as e^1?
-For specific values like e^1, the lecture describes computing e^x by summing the series: 1 + 1 + 1/2 + 1/6 + 1/24 + ... which converges to the familiar decimal expansion of e.
How does the lecture explain the differentiation of the exponential function e^x?
-The lecture explains that differentiating e^x, thought of as a long polynomial, results in the same series: e^x, showing that the function is its own derivative.
What happens when integrating the exponential function e^x according to the lecture?
-When integrating e^x, the lecture shows that it results in e^x minus a constant, which when simplified and considering the arbitrary constant, confirms that the integral of e^x is e^x up to a constant.
How are the trigonometric functions cosine and sine represented using the exponential function e^(ix) in the lecture?
-Using the definition of e^(ix) and simplifying, the real part of the expression gives the series for cos(x), and the imaginary part gives the series for sin(x).
What is the derived series expression for cosine as explained in the lecture?
-The series expression for cosine is cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ..., which can be written compactly using summation notation.
What is the series expression for sine derived in the lecture?
-The series expression for sine is sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ..., also represented compactly using summation notation.
How does the lecture verify the differentiation properties of sine and cosine?
-The lecture verifies the differentiation properties by showing that differentiating the series for sin(x) yields the series for cos(x), and differentiating the series for cos(x) yields -sin(x), consistent with their known calculus properties.
Outlines
📚 Introduction to Exponential Functions and Euler's Formula
Professor Greist begins Lecture Two by introducing the exponential function as the main character of calculus. The lecture delves into the definition of e^x, exploring its properties and implications. It also touches on the complexities of exponentiating irrational and complex numbers, as well as the derivative. The professor emphasizes that e^x is unique in being its own derivative and integral. Euler's formula, e^(i*x) = cos(x) + i*sin(x), is highlighted as a key to understanding complex exponentiation. The definition of e^x is presented as an infinite series involving factorials, which is a formula crucial for the course. The lecture concludes with an exploration of the implications of this definition for specific values of x, like x = 1, and how it converges to the known decimal expansion of e.
🔍 Differentiation and Integration of Exponential Functions
In this section, the focus shifts to the differentiation and integration of e^x using its polynomial-like definition. The professor explains how the derivatives of polynomials translate to the derivatives of e^x, resulting in the function itself. Similarly, the integration of e^x is explored, revealing that it results in e^x minus a constant, aligning with the expected integral properties. The lecture also revisits Euler's formula in the context of complex numbers, demonstrating how the powers of i lead to a pattern that simplifies the expression into real and imaginary components, directly relating to cosine and sine functions. This exploration showcases the interconnectedness of exponential and trigonometric functions within calculus.
🌐 Trigonometric Functions and Their Series Representations
The final paragraph of the script discusses the trigonometric functions sine and cosine, presenting new series representations derived from the exponential function. The professor simplifies the complex expression of e^(i*x) into real and imaginary parts, which correspond to cosine and sine, respectively. These parts are then expressed in summation notation, incorporating alternating signs and powers of x. The lecture demonstrates how these new expressions for sine and cosine can be differentiated to yield results consistent with known calculus properties, such as the derivative of sine being cosine. The professor encourages students to review these concepts in a bonus lecture for a more concrete understanding, setting the stage for the next lesson on series representations of a broader range of functions.
Mindmap
Keywords
💡Exponential function
💡Euler's formula
💡Factorial
💡Series expansion
💡Derivative
💡Integral
💡Polynomial
💡Complex number
💡Trigonometric functions
💡Summation notation
Highlights
Introduction of the exponential function as the principal hero of calculus.
Exploration of the exponential function's properties, including its own derivative and integral.
Euler's formula linking the exponential function with trigonometric functions.
Definition of e^x using an infinite series involving factorial notation.
Explanation of the significance of factorial in the definition of e^x.
Differentiation of e^x by treating it as an infinite polynomial.
Integration of e^x and the recovery of the original function with a constant of integration.
Application of the definition of e^x to complex numbers, specifically e^(i*x).
Simplification of e^(i*x) leading to expressions for cosine and sine in terms of the exponential function.
Derivation of trigonometric identities for cosine and sine using the exponential function.
Differentiation of the derived expressions for cosine and sine, yielding new insights into their relationships.
Discussion on the practical applications and implications of the exponential function in various mathematical contexts.
Emphasis on the importance of memorizing the formula for e^x for its utility throughout the course.
Illustration of how to handle infinite sums by treating them as long polynomials in calculus.
Introduction of a series perspective for a broader array of functions in the upcoming lesson.
Encouragement to watch a bonus lecture for a more concrete perspective on the exponential function.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: