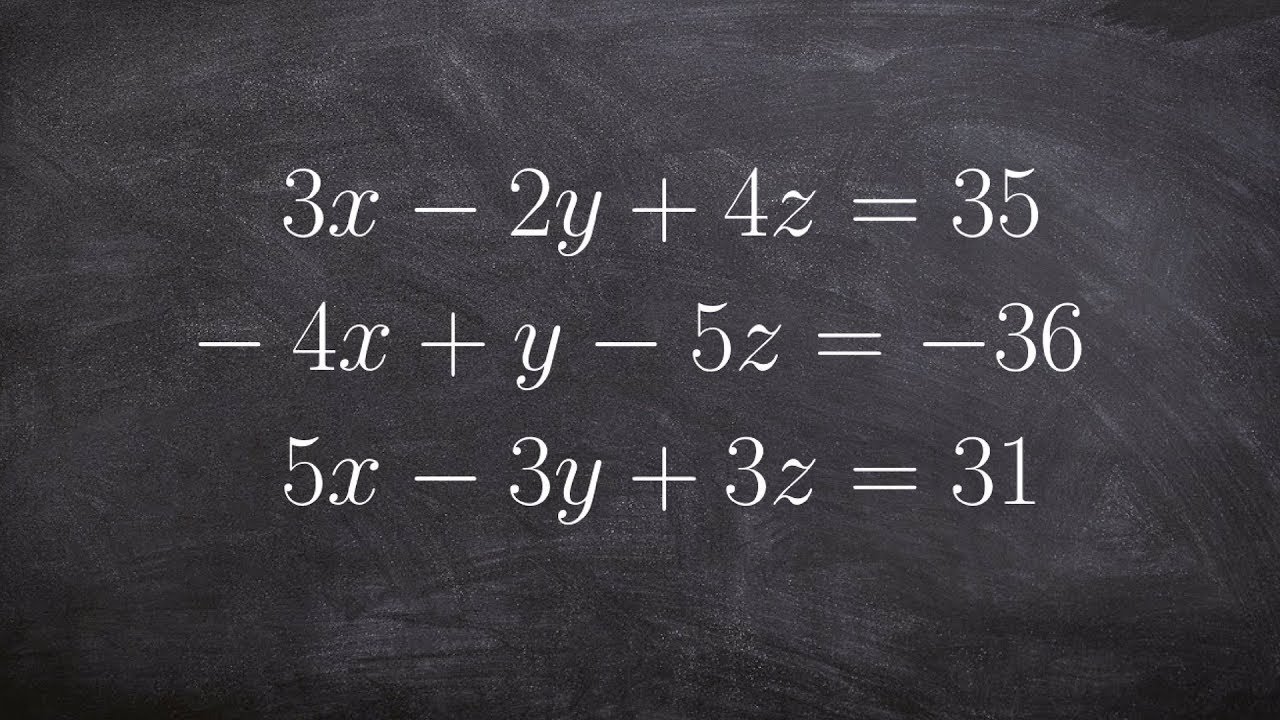Algebraic Equations With Variables on Both Sides
TLDRThe video script provides step-by-step examples for solving increasingly complex algebraic equations. It emphasizes developing strategies to manipulate equations to isolate the variable, first combining like terms before dividing. It walks through sample equations, highlighting the order of operations for addition/subtraction before multiplication/division. The script notes that while some equations require multiple strategic steps, meticulously moving through each one while carefully performing arithmetic often leads to the solution.
Takeaways
- 😀 When solving equations, do addition/subtraction before multiplication/division
- 😊 Combine like terms before doing other operations when possible
- 🧐 Develop a step-by-step strategy for solving complex equations
- 😎 Getting better at algebra takes practice
- 🤓 Manipulate equations to get the variable term isolated on one side
- 🤔 Changing form of equations may be needed to make them solvable
- 😇 Be meticulous when moving through each step of a multi-step solution
- 🙂 Simplify fractions in equations before combining terms
- 😜 Equations can be flipped to get variable on preferred side
- 🤩 Individual steps may be easy even if overall strategy is complex
Q & A
What should be done first when solving equations with multiple terms - addition/subtraction or multiplication/division?
-When solving algebraic equations, addition and subtraction should typically be done before multiplication and division.
What is the strategy when solving equations with multiple terms containing the same variable?
-The strategy is to perform operations to get all the terms containing the variable together on one side first.
How can you simplify conceptualizing multiplying or dividing both sides of an equation by a number?
-Instead of actually performing the multiplication or division, you can conceptually 'pull' the number from the denominator on one side to the numerator on the other side.
Why is it preferred to have the variable term on the left side when solving equations?
-Having the variable term on the left side makes equations easier to read and conceptualize when solving for the variable.
Even though individual steps may be easy, why can solving equations still be tricky?
-Solving equations can require developing a multi-step strategy, which means more opportunities to make a mistake. Careful, meticulous work is required at each step.
What is an example equation requiring multiple steps to solve?
-The equation provided in the last example requires distributing, eliminating fractions, combining like terms, and flipping sides - so multiple steps.
What is the purpose of simplifying conceptualization when solving equations?
-Simplifying conceptualization makes solving easier by avoiding extra arithmetic steps like writing multiplication, canceling terms, etc.
Why combine like terms before doing other operations?
-Combining like terms simplifies the equation first, allowing easier subsequent manipulations.
What is meant by carefully following each step when solving equations?
-It means consciously thinking through and correctly performing each arithmetic operation required by the strategy.
Why practice lots of examples when learning algebra?
-Practicing many examples helps develop proficiency and skill in conceptualizing and implementing solving strategies.
Outlines
📝 Learning to Solve More Complex Algebraic Equations
This paragraph introduces the topic of solving more complex algebraic equations. It explains that as equations get more complex, the strategies needed to solve them also get more complex. It emphasizes the importance of practice and provides some examples of trickier equations to solve.
🧮 Demonstrating Multi-Step Equation Solving
This paragraph checks comprehension on solving complex algebraic equations. It summarizes that these types of problems often require developing a multi-step strategy and carefully carrying out arithmetic at each step. It encourages meticulous work to successfully find solutions.
Mindmap
Keywords
💡algebraic equations
💡like terms
💡distribute
💡numerator
💡denominator
💡simplify
💡multiply
💡subtract
💡divide
💡strategy
Highlights
We have equations which contain one or more variables, and we can solve for these variables by manipulating the equation in various ways.
As the equations get more complex, the strategies we need to utilize to solve these equations will get more complex.
When solving equations, we should typically do addition and subtraction before multiplication and division.
When there is more than one term with the same variable, our strategy should be to combine those terms first.
We can combine like terms by adding or subtracting the coefficients of the terms with the same variable.
To remove a fraction on one side of an equation, we can multiply both sides by the denominator.
We may have to develop a multi-step strategy to solve an equation, with lots of opportunities for mistakes, but being meticulous in each step allows us to find the solution.
Addition and subtraction should typically be done before multiplication and division.
Combine like terms first when there are multiple terms with the same variable.
Coefficients of like terms can be combined by addition/subtraction.
Multiply both sides by a fraction's denominator to eliminate it.
Multi-step solutions require developing a strategy and meticulous step-by-step work.
Order of operations is addition/subtraction before multiplication/division.
Group like terms first when solving equations.
Careful arithmetic at each step allows complex multi-step solutions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: