Algebra - How To Solve Equations Quickly!
TLDRThis instructional video script offers a comprehensive guide on solving two-step equations, covering a variety of scenarios including equations with fractions, parentheses, variables on both sides, and even decimals. The transcript walks through the process of isolating variables, performing opposite operations such as subtraction and division, and combining like terms. It also touches on handling equations with multiple variables and parentheses, using the distributive property, and eliminating fractions by finding common multiples. The script concludes with a suggestion to explore an algebra course on Udemy for further learning, highlighting its structured content covering arithmetic, fractions, linear equations, inequalities, polynomials, factoring, systems of equations, quadratic equations, and more.
Takeaways
- 📚 The video focuses on solving two-step equations, covering various types including those with fractions, parentheses, variables on both sides, and decimals.
- 🔍 To isolate the variable 'x', the first step often involves performing the opposite operation to eliminate constants or coefficients from one side of the equation.
- ➖ Subtraction is used to eliminate constants on the same side as the variable, simplifying the equation to a form where the variable can be isolated.
- ➗ Division is used to separate the variable from its coefficient, allowing the solution for 'x' to be found.
- 🔄 The process of solving equations may require combining like terms and moving variables to one side of the equation to consolidate terms.
- 📉 When equations have variables on both sides, the goal is to move all variable terms to one side and constants to the other, simplifying the equation to solve for 'x'.
- 📌 The distributive property is essential for solving equations with parentheses, as it allows for the simplification of expressions within the parentheses.
- 📈 To eliminate fractions from equations, multiplying every term by the least common multiple (LCM) of the denominators is a common approach.
- 🔢 Dealing with decimals involves either solving the equation directly or multiplying every term by a power of 10 to eliminate the decimal places, simplifying the process.
- 📉 When encountering complex equations with multiple variables and fractions, systematically isolating the variable 'x' by moving terms and combining like terms is key.
- 📚 The video also mentions an algebra course on Udemy that covers a wide range of topics from basic arithmetic to complex algebraic concepts, including quizzes for each section.
Q & A
How do you solve a basic two-step equation like 3x + 5 = 17?
-To solve the equation 3x + 5 = 17, first subtract 5 from both sides to isolate the term with the variable, resulting in 3x = 12. Then, divide both sides by 3 to solve for x, which gives x = 4.
What is the first step in solving the equation 17 - 5x = 2?
-The first step in solving 17 - 5x = 2 is to subtract 17 from both sides to eliminate the constant term on the left side, resulting in -5x = -15.
How do you handle a fraction in an equation like 9 = 3 + x/4?
-To handle the fraction in 9 = 3 + x/4, subtract 3 from both sides to get 6 = x/4. Then multiply both sides by 4 to eliminate the fraction, which gives 24 = x.
What should you do when you encounter parentheses in an equation?
-When encountering parentheses, use the distributive property to multiply the term outside the parentheses by each term inside. Then combine like terms and proceed with solving the equation.
How do you solve an equation with multiple x variables like 3x + 8 + 5x = 32?
-Combine like terms first by adding 3x and 5x to get 8x. Then subtract 8 from both sides to isolate the variable terms, resulting in 8x = 24. Finally, divide by 8 to solve for x, which gives x = 3.
What is the process for solving an equation with variables on both sides?
-To solve an equation with variables on both sides, move all variable terms to one side using addition or subtraction, and all constant terms to the other side. Then, isolate the variable and solve for its value.
How do you deal with decimals in an equation like 2x + 0.3 = 1.5?
-To deal with decimals, you can either solve the equation directly or eliminate all decimals by multiplying every term by a power of 10 that moves the decimal point to the right, making it easier to solve.
What is a common strategy for solving equations with fractions?
-A common strategy for solving equations with fractions is to find a common multiple of the denominators and multiply every term by that number to eliminate the fractions.
How do you approach an equation with multiple fractions?
-For equations with multiple fractions, find the least common multiple (LCM) of the denominators and multiply every term by that LCM to eliminate all fractions before solving.
What is the final step in solving a two-step equation?
-The final step in solving a two-step equation is to isolate the variable by performing the opposite operation of what's affecting the variable (such as dividing if the operation was multiplying).
Outlines
📚 Introduction to Solving Two-Step Equations
This paragraph introduces the topic of solving two-step equations, covering basics such as equations with fractions, parentheses, variables on both sides, and decimals. The speaker begins by demonstrating how to solve a simple equation, 3x + 5 = 17, through the process of isolating the variable x. The explanation includes subtracting 5 from both sides to eliminate the constant term and then dividing by 3 to find the value of x, which is 4. The paragraph continues with similar examples, such as 4x + 3 = 19 and 17 - 5x = 2, illustrating the steps of subtraction and division to solve for x. The examples aim to teach viewers how to manipulate equations to isolate the variable and find the solution.
🔍 Advanced Two-Step Equations with Variables on Both Sides
This paragraph delves into more complex two-step equations where variables are present on both sides of the equation. The speaker provides a step-by-step guide on how to approach these problems, emphasizing the importance of moving all variable terms to one side and constants to the other. Examples given include equations like 9 = 3 + x/4 and 8 + x/3 = 12, where the speaker demonstrates subtracting constants and multiplying both sides to eliminate fractions and isolate the variable. The paragraph also covers scenarios with multiple x terms, such as 3x + 8 + 5x = 32, and shows how to combine like terms before solving. The goal is to simplify the equation into a form that can be easily solved by standard algebraic methods.
📘 Solving Equations with Parentheses and Distributive Property
The focus of this paragraph is on solving equations that include parentheses, which often require the use of the distributive property. The speaker explains how to distribute a term across parentheses and then combine like terms to simplify the equation. Examples such as 3 * (2x - 4) + 1 = 7 and 5 * (3x + 4) = 37 + 2 are used to illustrate the process. The speaker shows how to multiply through the parentheses, combine constants, and then isolate the variable term to solve for x. This paragraph helps viewers understand how to handle more complex algebraic expressions involving parentheses and demonstrates the systematic approach to solving such equations.
🎯 Mastering Equations with Multiple Fractions and Decimals
This paragraph addresses the challenge of solving equations that contain multiple fractions or decimals. The speaker introduces strategies for dealing with fractions, such as finding a common multiple to eliminate them, as shown in the example with two fractions. For decimals, the approach involves multiplying through by a power of 10 to clear the decimal points. The speaker provides examples with step-by-step solutions, such as multiplying every term by 6 to clear fractions in one equation and by 10 to eliminate decimals in another. The goal is to simplify the equations to a form where standard algebraic methods can be applied to find the value of x.
🏆 Comprehensive Algebra Course Overview
In the final paragraph, the speaker transitions from solving equations to promoting an algebra course available on Udemy. The course is described as covering a wide range of topics from basic arithmetic to more advanced algebraic concepts. The speaker outlines the course content, which includes sections on fractions, linear equations, order of operations, graphing linear equations, inequalities, polynomials, factoring, systems of equations, quadratic equations, rational and radical expressions, complex and imaginary numbers, exponential and logarithmic functions, conic sections, and sequences and series. Each section is said to include video quizzes for review. The speaker invites viewers to explore the course and provides a direct link to it on Udemy, aiming to support those who wish to deepen their understanding of algebra.
Mindmap
Keywords
💡Two-step equations
💡Isolate the variable
💡Opposite operation
💡Combine like terms
💡Distributive property
💡Fractions in equations
💡Decimals in equations
💡Checking your work
💡Multi-step equations
💡Common denominator
Highlights
Introduction to solving two-step equations with various complexities.
Basic approach to solving equations with fractions and parentheses.
Technique for isolating the variable 'X' in an equation.
How to handle equations with variables on both sides.
Dealing with decimals in equations by eliminating them.
Solving equations with multiple 'X' variables by combining like terms.
Method for moving all 'X' variables to one side of the equation.
Using the distributive property to simplify equations with parentheses.
Approach for solving equations with parentheses on both sides.
Eliminating fractions by finding a common multiple.
Strategy for equations with multiple fractions.
Solving equations with decimals by multiplying to eliminate them.
Technique for dealing with large numbers in equations by scaling.
Course recommendation for further study on algebra topics.
Overview of the algebra course content available on Udemy.
Description of the course sections covering arithmetic, fractions, and linear equations.
Mention of quizzes available in the course for each section.
Discussion on topics like inequalities, absolute value expressions, and polynomials.
Coverage of advanced topics like complex numbers, exponential functions, and logarithms.
Inclusion of conic sections, sequences, and series in the course curriculum.
Transcripts
Browse More Related Video

Substitution Method For Solving Systems of Linear Equations, 2 and 3 Variables, Algebra 2

College Algebra Introduction Review - Basic Overview, Study Guide, Examples & Practice Problems
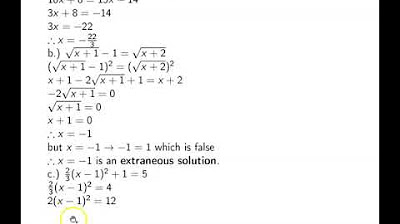
Ch. 1.5 Equations

Solving Polynomial and Rational Equations

01 - Introduction to the Algebraic Method for Balancing Chemical Equations

How to Rearrange Equations in Chemistry
5.0 / 5 (0 votes)
Thanks for rating: