Calculus AB/BC – 1.9 Connecting Multiple Representations of Limits
TLDRIn this calculus lesson, Mr. Bean guides students through understanding piecewise functions, tables of values, and graph interpretations, focusing on identifying when a limit does not exist. He demonstrates how to analyze linear functions and their limits by comparing left and right approaches. The lesson also covers handling limits with absolute values, showing how to plug in numbers close to the limit point to determine the outcome. This concise lesson is designed to connect different mathematical concepts for a deeper understanding of limits.
Takeaways
- 📚 The lesson is focused on connecting different representations of calculus concepts, emphasizing the importance of understanding piecewise functions, tables of values, and graphs.
- 🔍 Mr. Bean introduces a piecewise linear function with a non-existent limit as x approaches 5, highlighting the need to identify which representations match this characteristic.
- 📈 The graph representation is the easiest to analyze for the non-existence of a limit, as it visually shows the left and right limits not aligning.
- 📝 For piecewise functions, algebraic substitution is necessary to determine if the left and right limits exist and are equal, which in this case, they are not.
- 📊 The table of values approach requires examining the y-values as x approaches a certain value from both the left and right, to see if they converge to the same limit.
- 🤔 The lesson emphasizes the importance of understanding why certain limits do not exist, providing reasoning for each conclusion drawn from the different representations.
- 📐 When dealing with absolute values in limits, it's crucial to plug in numbers very close to the value you're approaching to see how the function behaves near that point.
- 🧩 The lesson connects the concept of limits with absolute values by demonstrating how to calculate the limit when an absolute value is involved in the function.
- 📉 In the absolute value example, plugging in a number close to 4 on the left side of the limit reveals that the function approaches -1, illustrating the process of evaluating limits with absolute values.
- 📚 The lesson is designed to be a quick and easy review, reinforcing the understanding of limits in various mathematical representations.
- 🎓 The mastery check at the end of the lesson serves as a tool for students to assess their understanding of the material covered.
Q & A
What is the main topic of Mr. Bean's calculus lesson?
-The main topic of the lesson is to connect different representations of functions, such as piecewise functions, tables of values, and graphs, with a focus on understanding the existence of limits.
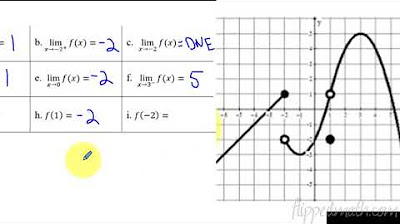
Why does the first graph provided in the lesson indicate that the limit does not exist as X approaches 5?
-The first graph shows that the left and right-sided limits are not equal as X approaches 5, which is why the limit does not exist.
What is the algebraic approach to determine if the limit exists for the second piecewise function?
-The algebraic approach involves substituting the value of X into both the left and right parts of the piecewise function and checking if they yield the same result.
How does the table of values indicate that the limit does not exist as X approaches 5 for the third example?
-The table of values shows that the y-values are approaching different values from the left and right sides of X=5, indicating that the limit does not exist.
What is the significance of the absolute value in the context of finding limits?
-The absolute value can affect the limit by changing the sign of the expression within it, which may influence whether the limit exists or not.
How does Mr. Bean suggest finding the limit when an absolute value is involved?
-Mr. Bean suggests plugging in numbers very close to the value you are approaching, such as 3.999 for X approaching 4, to determine the behavior of the function near that point.
What is the result of the limit as X approaches 4 in the example involving an absolute value?
-The result of the limit as X approaches 4 in the given example is -1, due to the absolute value of a small negative number divided by the same small negative number.
Why are the left and right-sided limits important in determining the existence of a limit?
-The left and right-sided limits are important because if they are not equal, it indicates that the limit does not exist at that point.
What does Mr. Bean mean by 'putting a bunch of things together' in the context of this lesson?
-Mr. Bean is referring to the integration of different mathematical concepts and representations to understand and analyze the behavior of functions, especially in relation to limits.
How does the lesson emphasize the importance of understanding limits in calculus?
-The lesson emphasizes the importance of understanding limits by showing various ways to determine if a limit exists, including graphical, algebraic, and tabular methods.
Outlines
📚 Calculus Lesson with Mr. Bean
In this lesson, Mr. Bean introduces a calculus problem involving piecewise functions, tables of values, and graphs. The main focus is on understanding when a limit does not exist. The instructor explains how to identify such cases by examining the left and right limits of a function, particularly for a piecewise linear function. The lesson demonstrates how to check if the left and right limits match, and if they don't, it indicates the limit does not exist. The instructor also covers how to handle limits with absolute values by plugging in numbers close to the point of interest and simplifying the expression to find the limit.
🎶 Background Music
This paragraph is simply a placeholder for background music that plays during the video, providing an auditory backdrop to the educational content. It does not contain any spoken words or additional information, serving to enhance the overall viewing experience.
Mindmap
Keywords
💡Calculus
💡Piecewise Function
💡Limit
💡Graph
💡Table of Values
💡Left-sided Limit
💡Right-sided Limit
💡Absolute Value
💡Linear Function
💡Mastery Check
Highlights
Introduction to a calculus lesson by Mr. Bean focusing on connecting different mathematical representations.
Explanation of a piecewise linear function with a non-existent limit as X approaches 5.
Graphical analysis to determine the non-existence of a limit by observing the left and right side of the graph.
Algebraic substitution to check the limit of a piecewise function by plugging in values.
Determination that the limit exists for a piecewise function where left and right sides approach the same value.
Use of a table of values to analyze the behavior of a function as it approaches a certain point.
Identification of a table of values where the left and right limits do not match, indicating a non-existent limit.
Discussion on the practical application of limits in today's practice problems.
Introduction of a method to find limits involving absolute values without a graph.
Technique of plugging in numbers close to the limit point to determine the behavior of an absolute value function.
Explanation of how to handle absolute values in limits by simplifying the expression with close numbers.
Conclusion that the limit of an absolute value function approaches a negative value when the numerator and denominator are close to zero.
Emphasis on the importance of understanding limits, especially with absolute values, for AP exam preparation.
Brief overview of the lesson's content, highlighting the quick and easy nature of the material.
Encouragement for students to master the concepts discussed in the lesson.
Anticipation of a mastery check and a follow-up lesson to reinforce the material.
Transcripts
Browse More Related Video

Calculus AB/BC – 1.14 Infinite Limits and Vertical Asymptotes

AP Calculus AB - 1.9 Connecting Multiple Representations of Limits

Calculus AB/BC – 1.5 Determining Limits Using Algebraic Properties
Calculus AB/BC – 1.3 Estimating Limit Values from Graphs
How To Tell If The Limit Exists

Calculus - One Sided Limits
5.0 / 5 (0 votes)
Thanks for rating: