Calculus - One Sided Limits
TLDRThe lesson delves into one-sided limits, a concept where the limit of a function as it approaches a certain point from the left or right may differ, leading to discontinuity. The instructor explains how to denote and calculate these limits, using the superscript of a minus or plus sign to indicate direction. Examples illustrate scenarios where limits exist or do not, including the behavior of the absolute value function. A problem-solving approach is demonstrated to find a value of 'k' that ensures a limit's existence, emphasizing the importance of understanding piecewise functions and absolute values in calculus.
Takeaways
- 📚 The lesson focuses on understanding one-sided limits and their importance in evaluating limits at points of discontinuity.
- 👉 The notation for left-hand limit is written as \( \lim_{x \to 3^-} f(x) \), indicating approach from the left side.
- 👈 The notation for right-hand limit is written as \( \lim_{x \to 3^+} f(x) \), indicating approach from the right side.
- 🔄 If the left and right limits at a point are not equal, the overall limit at that point does not exist.
- 🔄 Conversely, if the left and right limits are equal, the overall limit exists and is equal to that common value.
- 📉 The function's value at a point is independent of the left or right limit; the function's value is the actual output of the function at that point.
- 📈 The concept of the absolute value function is revisited, showing its piecewise definition and graphical representation.
- 🤔 The lesson includes examples to illustrate how to determine if a limit exists by comparing left and right limits.
- 📝 The importance of understanding the behavior of functions as they approach certain values from both sides is emphasized for determining limits.
- 🔢 A specific problem-solving strategy is demonstrated to find the value of 'k' that makes a limit exist by ensuring the function is continuous at a certain point.
- ✅ The lesson concludes with a reminder to practice these concepts and to understand the role of the absolute value function in limit problems.
Q & A
What is the concept of one-sided limits in calculus?
-One-sided limits refer to the behavior of a function as the input approaches a certain value from either the left or the right side. It is denoted as the limit from the left (with a superscript minus sign) or from the right (with a superscript plus sign).
Why is it important to consider one-sided limits?
-One-sided limits are important because they help determine the behavior of a function at points of discontinuity, where the function may approach different values from the left and right sides.
What happens when the one-sided limits from the left and right do not equal each other?
-If the one-sided limits from the left and right do not equal each other, it indicates that the limit at that point does not exist, as the function does not approach a single value as the input approaches from either side.
How can you denote the limit as x approaches a certain value from the left?
-The limit as x approaches a certain value from the left is denoted by placing a superscript minus sign after the value, such as \( \lim_{x \to a^-} \).
What is the notation for the limit as x approaches a certain value from the right?
-The limit as x approaches a certain value from the right is denoted by placing a superscript plus sign after the value, such as \( \lim_{x \to a^+} \).
What is the difference between the limit at a point and the function's value at that point?
-The limit at a point is the value the function approaches as the input gets arbitrarily close to that point, whereas the function's value at that point is the actual output of the function when the input is exactly at that point.
How does the absolute value function behave at points where x is negative?
-For the absolute value function, when x is negative, the function outputs the negation of x, effectively making the output positive by multiplying the negative x by -1.
What is the definition of the absolute value function?
-The absolute value function is defined piecewise, where it outputs x if x is greater than or equal to zero, and outputs -x if x is less than zero.
Why is it necessary to factor expressions when evaluating limits involving polynomials?
-Factoring expressions can simplify the process of evaluating limits, especially when the limit involves a rational function, as it may reveal factors that cancel out, making it easier to determine the limit's value.
What is the significance of finding the value of k in the given script's example?
-The value of k is significant because it determines whether the limit of the given expression exists. By finding the correct value of k, the expression can be simplified to a form where the limit from the left and right sides are equal, thus ensuring the limit exists.
How can you determine if a limit exists for a rational function?
-A limit exists for a rational function if the limit from the left and the limit from the right are equal. This requires the function to approach the same value as the input gets arbitrarily close to the point from both sides.
Outlines
📚 Introduction to One-Sided Limits
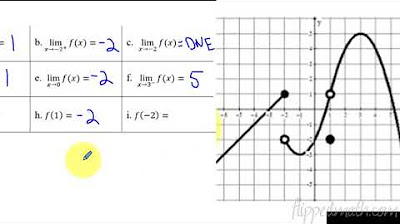
This paragraph introduces the concept of one-sided limits, which are limits taken as a variable approaches a certain value from either the left or right side. The importance of one-sided limits is highlighted in cases where a function has a discontinuity at a point, as seen with the function approaching different values from each side of the point x=3. The notation for left and right limits is explained, with the use of superscripts to indicate the direction of approach. The paragraph also clarifies that a limit exists only if both one-sided limits are equal to the same value, otherwise, the limit does not exist. Examples are given to illustrate the concept, including a function with a discontinuity at x=3 and another at x=1, where the function approaches different values from the left and right.
📈 Understanding Absolute Value Functions and Limits
The second paragraph delves into the specifics of the absolute value function, explaining its definition and graphical representation. It discusses how the absolute value behaves differently for positive and negative inputs, resulting in a 'V' shaped graph. The paragraph uses the absolute value function to explore the existence of limits as x approaches zero and other values, emphasizing the need for the left and right limits to be equal for the overall limit to exist. An example is given where the limit does not exist due to the left and right limits yielding different results. Additionally, the paragraph explores how to evaluate limits involving absolute values, such as approaching x=1 from both sides and demonstrating the process to find the limit.
🔍 Analyzing Limits and Factorization to Determine a Variable
The final paragraph presents a problem-solving approach to determine the value of a variable 'k' in a given expression to ensure the existence of a limit as x approaches -2. It explains the process of taking one-sided limits and the importance of factorization in simplifying expressions. The paragraph demonstrates how to identify a root of a polynomial to ensure the cancellation of terms in the numerator and denominator, leading to a determinable limit. The solution involves setting up an equation based on the condition that the polynomial has a root at x=-2, solving for 'k', and verifying the result by substituting the value back into the expression to confirm that the left and right limits are equal, thus proving the limit exists and is equal to -1.
Mindmap
Keywords
💡One-sided limits
💡Discontinuity
💡Limit notation
💡Left-hand limit
💡Right-hand limit
💡Absolute value function
💡Piecewise function
💡Continuity
💡Factoring
💡Roots of a polynomial
Highlights
Introduction to one-sided limits and their importance in calculus.
Explanation of discontinuity in a function and the concept of a jump or break in the graph.
Notation for left-hand and right-hand limits with examples.
Condition for the existence of a limit when left and right limits are equal.
Illustration of how to determine if a limit does not exist due to unequal left and right limits.
Example of evaluating limits for a function approaching a point from both sides.
Demonstration of how to find the limit as x approaches 1 and its existence.
Analysis of the limit as x approaches 3 from the left and right, showing non-existence due to different values.
Explanation of evaluating the function at a specific point versus finding the limit at that point.
Application of the absolute value function in limit problems and its piecewise definition.
Use of the absolute value function to find the limit as x approaches zero.
Counterexample showing the non-existence of a limit due to different left and right limits.
Method to evaluate limits involving absolute value expressions by considering different approaches to zero.
Determination of the value of k for which a limit exists in a given rational function expression.
Process of factoring and simplifying expressions to find the value of k that ensures limit existence.
Final conclusion on the value of k that makes the limit of the expression exist, which is 15.
Emphasis on understanding the absolute value function and its role in solving limit problems.
Encouragement for students to review concepts and practice on their own to solidify understanding.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: