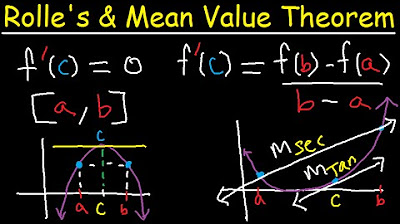Calculus AB Homework 5.2: Existence Theorems
TLDRThe video script offers a detailed walkthrough of applying the Mean Value Theorem and other calculus concepts to various functions. It covers determining the theorem's applicability, finding the value of C, and calculating derivatives and average rates of change. The script also discusses the conditions for the Mean Value Theorem, the Intermediate Value Theorem, and Rolle's Theorem, providing step-by-step analysis and graphical interpretations to solve problems involving functions like temperature change and bed occupancy in a hospital.
Takeaways
- 📚 The script discusses the Mean Value Theorem and its conditions for applicability to functions on specific intervals.
- 🔍 It emphasizes the importance of checking for continuity on a closed interval and differentiability on an open interval for the Mean Value Theorem to hold.
- 📉 The video provides a step-by-step analysis of a function to determine if it meets the criteria for the Mean Value Theorem, using the function f(x) = -2 + 0.5 * |x - 3| as an example.
- 📈 The script uses graphical analysis to determine differentiability, showcasing how the presence of a corner point affects the application of the Mean Value Theorem.
- 📝 It demonstrates how to find the derivative of a function using a calculator and explains the significance of the derivative in context, such as the rate of temperature change for a cup of coffee.
- 🏥 The script applies the Mean Value Theorem to a hospital bed occupancy function, illustrating how to find the rate of change in bed usage over time.
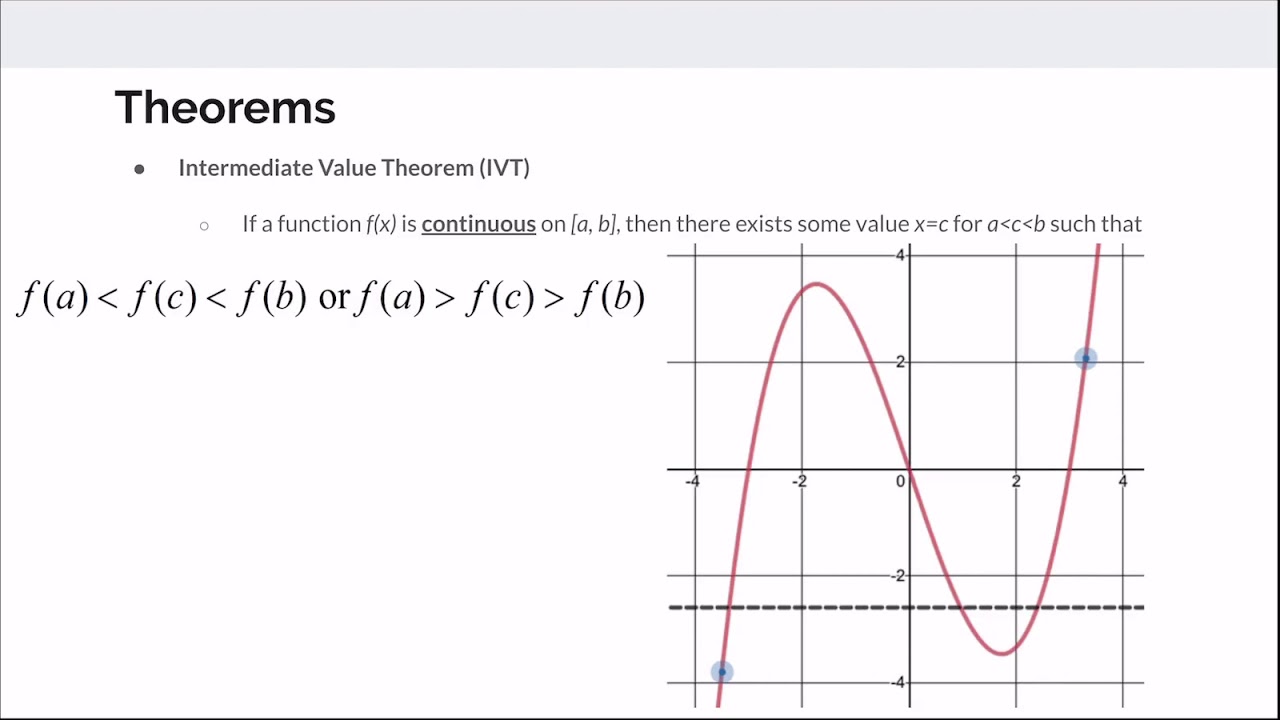
- 📊 The video uses a table of values to estimate derivatives and discusses the use of the Intermediate Value Theorem to guarantee the existence of certain function values within an interval.
- 🤔 The script introduces Rolle's Theorem as a special case of the Mean Value Theorem, requiring the function to be continuous and differentiable with equal y-coordinates at endpoints.
- 🔢 It guides through the process of finding intervals where the average rate of change equals a specific value, using the Mean Value Theorem to guarantee the existence of a derivative with that value.
- 📚 The final takeaway is the importance of verifying the conditions of theorems before applying them and understanding what each theorem guarantees about the function in question.
Q & A
What is the Mean Value Theorem and what conditions must be met for it to apply?
-The Mean Value Theorem states that if a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one point c in (a, b) such that the derivative at c is equal to the average rate of change of the function over the interval. The conditions are that the function must be continuous on the closed interval and differentiable on the open interval.
Why does the Mean Value Theorem not apply to the function f(x) = -2 + 1/2 * |x - 3| on the interval [0, 5]?
-The Mean Value Theorem does not apply because the function f(x) is not differentiable at x = 3, which is within the interval [0, 5]. The absolute value function has a corner point at x = 3, making the function non-differentiable at this point.
How can we determine if a function is continuous on a given interval?
-A function is continuous on a given interval if there are no breaks, jumps, or asymptotes in the graph of the function within that interval. It can be determined by visual inspection of the graph or by checking that the function's limit at every point in the interval exists and is equal to the function's value at that point.
What is the process to find the value of C guaranteed by the Mean Value Theorem for the function G(x) = 2x + sin^2(x) on the interval [0, 5]?
-To find the value of C, first confirm the function is continuous on the closed interval [0, 5] and differentiable on the open interval (0, 5). Then, calculate the average rate of change of G(x) over the interval, which is (G(5) - G(0))/(5 - 0). Next, find the derivative G'(x) and set it equal to the average rate of change to solve for the values of x (C) where the derivative equals the average rate of change.
How do you find the derivative of a function using a calculator?
-To find the derivative of a function using a calculator, first enter the function into the calculator. Then, use the calculator's derivative function, often labeled as 'Dx' or a similar notation, to calculate the derivative at a specific point or over an interval. For example, if the function is stored in Y1, you can use 'Y1' followed by the derivative function and the value at which you want to evaluate the derivative.
What does the negative value of the derivative indicate about the function?
-A negative value of the derivative indicates that the function is decreasing at the point where the derivative is evaluated. The rate at which the function is decreasing is given by the absolute value of the derivative.
How can you find the maximum number of beds in use on the interval [12, 20] using the function B(T) = 20 * sin(T/10) + 50?
-To find the maximum number of beds in use, first determine if the function B(T) is continuous and differentiable on the interval [12, 20]. Then, look for relative maximums on the graph of the function within the interval and compare them with the function values at the endpoints. The highest value among these will be the absolute maximum on the interval.
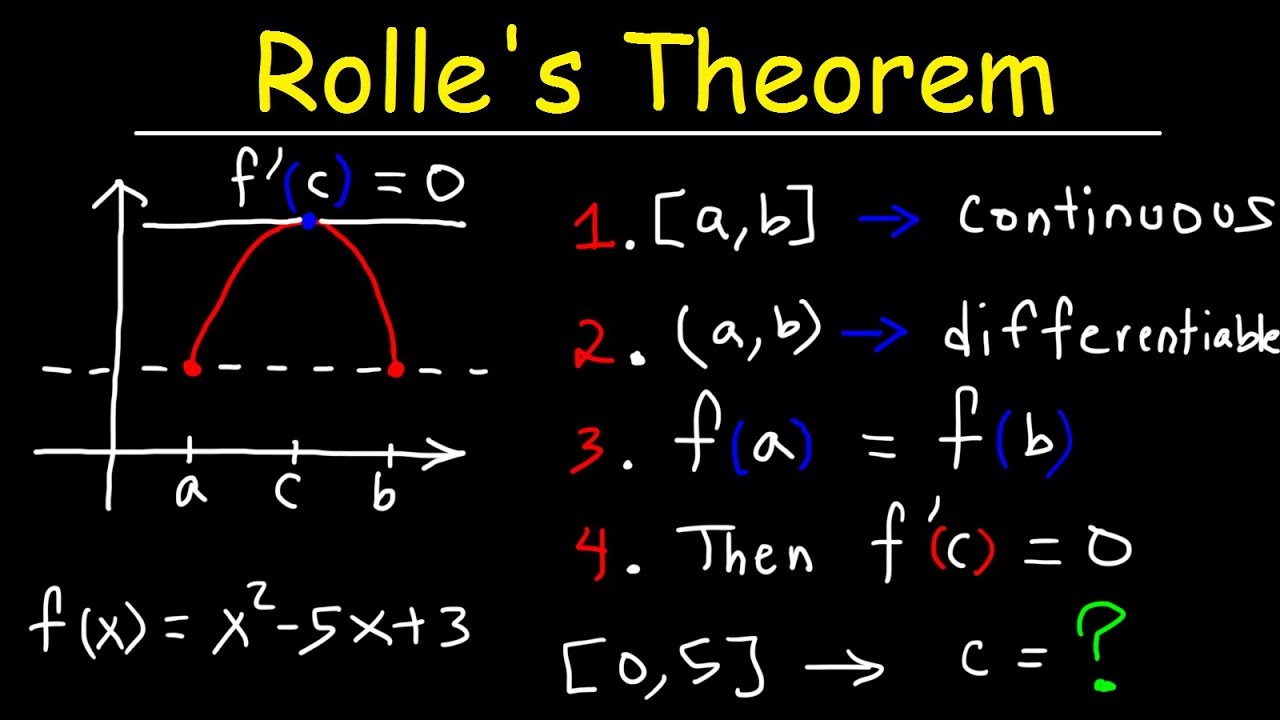
What is Rolle's Theorem and what are the conditions for it to hold?
-Rolle's Theorem states that if a function is continuous on a closed interval [a, b], differentiable on the open interval (a, b), and the function values at the endpoints are equal (f(a) = f(b)), then there exists at least one point c in (a, b) where the derivative of the function is zero. The conditions are continuity on the closed interval, differentiability on the open interval, and equal function values at the endpoints.
How do you estimate the value of a derivative at a specific point using a table of function values?
-To estimate the value of a derivative at a specific point using a table, find the two closest points to the desired point and calculate the average rate of change over the interval between these two points. This average rate of change is the best estimate for the instantaneous rate of change at the specific point.
What does it mean if the average rate of change of a function over an interval is 4?
-If the average rate of change of a function over an interval is 4, it means that the function is increasing or decreasing at a rate of 4 units per unit of the independent variable over that interval. According to the Mean Value Theorem, this implies that there is at least one point within the interval where the instantaneous rate of change (the derivative) is also 4.
How can you determine if a function will have a value equal to a specific number using the Intermediate Value Theorem?
-To determine if a function will have a value equal to a specific number using the Intermediate Value Theorem, ensure that the function is continuous on the interval in question. Then, find two points within the interval where the function values are less than and greater than the specific number, respectively. The theorem guarantees that there is at least one point between these two points where the function value equals the specific number.
Outlines
📚 Mean Value Theorem Application
This paragraph discusses the application of the Mean Value Theorem to two different functions. The first function, f(x) = -2 + 0.5 * |x-3|, is analyzed for continuity and differentiability on the interval [0, 5], concluding that the Mean Value Theorem does not apply due to non-differentiability at x=3. The second function, g(x) = 2x + sin^2(x), is confirmed to be both continuous and differentiable on the interval [0, 5], satisfying the conditions for the Mean Value Theorem. The value of C that guarantees the theorem's application is found by setting the derivative equal to the average rate of change over the interval, resulting in multiple points of intersection that satisfy the theorem.
🔍 Derivative Calculation and Interpretation
The paragraph focuses on calculating and interpreting derivatives in the context of specific problems. For a coffee temperature function, f(T) = 68 + 93 * 0.91^T, the derivative at T=4 is calculated using a calculator, resulting in a negative value indicating a decreasing temperature rate. For a hospital bed occupancy function, B(T) = 20 * sin(T/10) + 50, the derivative at T=7 is found, showing an increasing rate of bed occupancy. The paragraph emphasizes the importance of units of measure and the interpretation of derivative values in real-world contexts.
📈 Analyzing Bed Occupancy Function
This section involves a detailed analysis of the function representing the number of hospital beds in use, B(T) = 20 * sin(T/10) + 50, with T in days. The derivative B'(T) is calculated at T=7 to understand the rate of change in bed occupancy. The paragraph then shifts focus to finding the absolute maximum number of beds in use between days 12 and 20. By examining the graph and considering endpoints and relative maxima, it is determined that the maximum occupancy is 70 beds, occurring at T=15.708.
📊 Estimating Derivatives and Applying Theorems
The paragraph explores the estimation of the derivative of a function G at a specific point using the average rate of change between surrounding points. It also discusses the application of the Intermediate Value Theorem to guarantee the existence of a value C where G(C) equals -1, given the continuity of G on the interval from 0 to 6. Additionally, Rolle's Theorem is considered for finding a value C where the derivative equals zero, concluding that such a C exists on the interval from 2 to 6 due to the matching y-coordinates at the endpoints and the function's differentiability.
🔧 Applying Mean Value Theorem for Specific Derivative Values
This paragraph delves into the Mean Value Theorem to find intervals where the derivative of a function G equals specific values. It starts by identifying an interval where G' equals 4 by comparing average rates of change to the desired value. The theorem's conditions are verified: continuity on a closed interval and differentiability on an open interval. The conclusion is that there exists a C on the interval from 2 to 3 where G'(C) equals 4, satisfying the theorem's requirements.
Mindmap
Keywords
💡Mean Value Theorem
💡Differentiable
💡Continuous
💡Absolute Value
💡Derivative
💡Average Rate of Change
💡Rolle's Theorem
💡Intermediate Value Theorem
💡Graph
💡Endpoint
💡Instantaneous Rate of Change
Highlights
Introduction to working through Unit 5 homework problems 13 through 24.
Exploring the Mean Value Theorem for the function f(x) = -2 + 0.5 * |x - 3| on the interval [0, 5].
Requirement for the function to be continuous on the closed interval and differentiable on the open interval for the Mean Value Theorem to apply.
Analysis of the graph of f(x) to determine differentiability and continuity.
Conclusion that the Mean Value Theorem does not apply to f(x) due to non-differentiability at x = 3.
Investigation of the Mean Value Theorem for the function g(x) = 2x + sin^2(x) on the interval [0, 5].
Verification of the function g(x) being continuous and differentiable on the interval [0, 5].
Application of the Mean Value Theorem to find the guaranteed value of C for g(x).
Calculation of g'(x) using the derivative of sine squared x.
Determination of the average rate of change for g(x) and setting it equal to g'(x).
Finding multiple points of intersection indicating values of C that satisfy the theorem.
Problem 15 involves modeling the temperature of coffee with the function f(T) and finding f'(4).
Explanation of the negative value of f'(4) indicating the rate at which the coffee's temperature is decreasing.
Problem 16 examines the number of hospital beds in use with function B(T) and finding B'(7).
Interpretation of B'(7) as the rate of increase in the number of beds in use on day 7.
Problem 17 estimates G'(2.5) using the average rate of change between points on the interval [2, 3].
Application of the Intermediate Value Theorem in problem 18 to guarantee the existence of a value for G(x) equal to -1.
Rolle's Theorem is applied in problem 19 to guarantee the existence of a point where the derivative equals zero.
Problem 20 uses the Mean Value Theorem to find an interval where G'(x) equals 4.
Final summary emphasizing the importance of checking conditions and correctly applying theorems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: