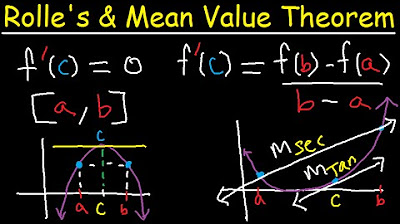Rolle's Theorem
TLDRThe video script offers an insightful exploration of Rolle's Theorem, a fundamental concept in calculus. It explains the theorem's main idea—that if a function is continuous on a closed interval and differentiable on the open interval, with the same value at the endpoints, there exists a point within the interval where the derivative is zero. The script supports this explanation with graphical examples and applies the theorem to various functions, demonstrating its applicability and limitations. The examples cover polynomial, sinusoidal, and power functions, as well as absolute value functions, highlighting the conditions for the theorem's use and the process for identifying points of interest.
Takeaways
- 📌 Rolle's Theorem states that if a function is continuous on a closed interval and differentiable on the open interval, with the same function values at the endpoints, there exists at least one point C in the interval where the derivative is zero.
- 📈 The function must satisfy three conditions for Rolle's Theorem to apply: continuity on the closed interval, differentiability on the open interval, and equal function values at the endpoints.
- 🔍 To apply Rolle's Theorem, one must verify the function's continuity and differentiability, and check if the function values at the interval's endpoints are equal.
- 🤔 The theorem does not apply if the function is not differentiable at some point within the interval, such as at sharp turns or cusps.
- 📊 Graphical examples help illustrate the theorem, showing where horizontal tangents exist and where the derivative equals zero.
- 👉 Examples include polynomial functions, which are continuous and differentiable everywhere, and thus can have Rolle's Theorem applied.
- 🌟 The theorem can be applied to find critical numbers by setting the first derivative equal to zero and solving for the variable.
- 🛠️ The product rule and chain rule are useful in finding the first derivative of composite functions, which is necessary to apply Rolle's Theorem.
- 🔢 The theorem can be used to approximate values within an interval where the horizontal tangent occurs, even if the exact value is a decimal.
- ❌ Functions with absolute value or sharp changes in derivative, such as at points of non-differentiability, do not satisfy the conditions for Rolle's Theorem.
Q & A
What is Rolle's Theorem and what are the three conditions that must be met for it to apply?
-Rolle's Theorem states that if a function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), with f(a) = f(b), then there exists at least one number c in (a, b) such that the derivative f'(c) is zero. The three conditions are: 1) the function must be continuous on [a, b], 2) the function must be differentiable on (a, b), and 3) f(a) must equal f(b).
How can you determine if a function is continuous on a given interval?
-A function is continuous on an interval if there are no breaks, jumps, or vertical asymptotes in the graph within that interval. It means the function can be traced without lifting the pen from the paper.
What does it mean for a function to be differentiable on an interval?
-A function is differentiable on an interval if its derivative can be calculated at every point within that interval, indicating that the function has a smooth, well-defined slope at each point.
What is the significance of the condition f(a) = f(b) in Rolle's Theorem?
-The condition f(a) = f(b) ensures that the function has the same value at the endpoints of the interval. This is important for the theorem because it implies that there must be at least one point in the interval where the function's rate of change is zero, leading to a horizontal tangent line.
How can you find the value of c that satisfies Rolle's Theorem?
-To find the value of c that satisfies Rolle's Theorem, you first need to ensure that all conditions of the theorem are met. Then, you find the first derivative of the function and set it equal to zero to solve for c, which is the point where the function has a horizontal tangent.
What happens if a function does not meet the second condition of Rolle's Theorem?
-If a function does not meet the second condition of Rolle's Theorem (i.e., it is not differentiable on the open interval), the theorem cannot be applied. For example, if there is a sharp turn or cusp in the graph, the function is not differentiable at that point, and Rolle's Theorem does not guarantee the existence of a horizontal tangent.
Can you provide an example of a function that does not meet the conditions of Rolle's Theorem?
-An example of a function that does not meet the conditions of Rolle's Theorem is f(x) = |x| on the interval [-1, 2]. This function is not differentiable at x = 1 due to the sharp turn in its graph, and thus, Rolle's Theorem does not apply.
How does the graph of a function that satisfies all conditions of Rolle's Theorem typically look?
-The graph of a function that satisfies all conditions of Rolle's Theorem will be continuous and without any breaks or vertical asymptotes on the closed interval [a, b]. It will also be differentiable on the open interval (a, b), with no sharp turns orcusps, and f(a) will equal f(b).
What is the role of the first derivative in applying Rolle's Theorem?
-The first derivative of the function plays a crucial role in applying Rolle's Theorem. It is used to find the critical points where the function might have a horizontal tangent, which is the condition for the existence of a point c that satisfies the theorem. By setting the first derivative equal to zero, we can find the potential values of c.
What is the product rule and how is it applied in differentiation?
-The product rule is a fundamental rule in differentiation that applies when differentiating a product of two functions. According to the product rule, if you have a function that is the product of two other functions, say u(x) and v(x), then the derivative of this function is given by u'(x)v(x) + u(x)v'(x). This means you differentiate each function separately and then add the product of the derivative of the first function with the second function and the product of the first function with the derivative of the second function.
How can you determine if a function has a horizontal tangent at a certain point?
-A function has a horizontal tangent at a certain point if the first derivative of the function at that point is zero. This means the slope of the tangent line to the graph of the function at that point is zero, indicating a horizontal line.
What is the significance of finding the point where f'(c) = 0 in Rolle's Theorem?
-Finding the point where f'(c) = 0 is significant in Rolle's Theorem because it is the point at which the function has a horizontal tangent. This point is of particular interest because it indicates a local extremum or a point of inflection in the function where the function's rate of change transitions from increasing to decreasing or vice versa.
Outlines
📚 Introduction to Rolle's Theorem and its Conditions
This paragraph introduces Rolle's Theorem, a fundamental concept in calculus. It explains that the theorem applies when a function f(x) is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), with f(a) = f(b). If these conditions are met, there exists at least one number c in the interval (a, b) where the derivative f'(c) is zero, indicating a horizontal tangent on the graph of the function. The explanation is accompanied by a graphical representation to illustrate the concept. The paragraph also provides an example to test the application of the theorem and emphasizes the importance of differentiability for the theorem to hold.
🔍 Applying Rolle's Theorem to Specific Functions
This paragraph delves into the application of Rolle's Theorem to various specific functions. It begins with a quadratic function, f(x) = x^2 - 5x + 3, on the interval [0, 5], confirming that the theorem can be applied as all conditions are met. The calculation shows that the function has the same value at the endpoints, and the first derivative equals zero at x = 2.5, within the interval. The paragraph then discusses the sine function on the interval [0, 2π], noting that there are two points, π/2 and 3π/2, where the derivative is zero, thus satisfying Rolle's Theorem. The discussion continues with examples of functions where the theorem does not apply, such as those with cusps or those not differentiable on the open interval, reinforcing the importance of the theorem's conditions.
🧮 Calculating the Point of Application for Rolle's Theorem
This paragraph focuses on the calculation of the specific point where Rolle's Theorem applies. It presents a function, f(x) = x * √(4 - x), on the interval [0, 4], and confirms that the theorem is applicable. The process of finding the first derivative using the product rule is detailed, leading to the calculation of the critical point where the derivative equals zero. The explanation includes the steps of factoring out the greatest common factor and applying the chain rule to find the derivative. The final calculation shows that the value of x, and thus the point of application for Rolle's Theorem, is approximately 2.67.
🚫 Functions Where Rolle's Theorem Does Not Apply
This paragraph discusses functions to which Rolle's Theorem cannot be applied. It starts with a function involving a square root, x^(2/3) + 1, on the interval [-4, -4], noting that the graph has a cusp at x = 0, making it non-differentiable at that point and thus ineligible for the theorem. The paragraph then examines an absolute value function, |x - 1|, on the interval [-1, 2], highlighting that it is not differentiable at x = 1 due to a sharp turn, and therefore, Rolle's Theorem does not apply. The explanation emphasizes the necessity of differentiability and the absence of sharp turns or cusps for the theorem to be applicable.
Mindmap
Keywords
💡Rolle's Theorem
💡Continuous Function
💡Differentiable Function
💡Closed Interval
💡Open Interval
💡Horizontal Tangent
💡Derivative
💡Critical Number
💡Polynomial Function
💡Sinusoidal Function
💡Absolute Value Function
Highlights
Rolle's Theorem is introduced with a focus on its application through example problems.
A function must be continuous on a closed interval and differentiable on the open interval to satisfy Rolle's Theorem conditions.
Rolle's Theorem states that if a function meets certain conditions, there exists a point with a horizontal tangent between the interval.
The theorem is visually illustrated with a graph example, showing a function that meets all conditions.
An example of a function that does not meet the differentiability condition of Rolle's Theorem is provided, with a graphical explanation.
A quadratic function is used as an example to demonstrate the application of Rolle's Theorem, with a step-by-step analysis.
The sine function is analyzed over a specific interval, showing that Rolle's Theorem can be applied twice due to its periodic nature.
A function with a cusp is shown to not meet the criteria for Rolle's Theorem due to the lack of differentiability at a certain point.
A function involving a square root and polynomial is examined for Rolle's Theorem applicability with a graphical sketch.
The application of Rolle's Theorem is confirmed for the given function, with the calculation of the first derivative and the critical point.
An absolute value function is discussed, explaining why it does not meet the criteria for Rolle's Theorem due to the lack of differentiability at a specific point.
The importance of differentiability for the application of Rolle's Theorem is emphasized through the examples of functions with and without sharp turns.
The process of finding the first derivative of a function to apply Rolle's Theorem is demonstrated with a detailed example.
The concept of horizontal tangent and its significance in Rolle's Theorem is clarified through various function examples.
The conditions for Rolle's Theorem are reiterated, highlighting the necessity of the function values at the interval endpoints being equal.
The graphical representation of functions helps in understanding the applicability of Rolle's Theorem and identifying critical points.
The video provides a comprehensive overview of Rolle's Theorem, including its conditions, implications, and examples of its application.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: