Rolle's Theorem Explained and Mean Value Theorem For Derivatives - Examples - Calculus

The Organic Chemistry Tutor

28 Sept 201633:46

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the Rolle's Theorem and Mean Value Theorem, focusing on their applications to various mathematical problems. It begins by explaining the conditions for Rolle's Theorem, which involves a function being continuous on a closed interval and differentiable on the open interval, with matching function values at the interval endpoints. The script then applies these concepts to several examples, including polynomial and rational functions, to find the value of 'c' where the derivative equals zero. The Mean Value Theorem is also discussed, highlighting its relationship with the slope of the tangent and secant lines. The video provides a comprehensive understanding of these theorems and their significance in calculus.

Takeaways

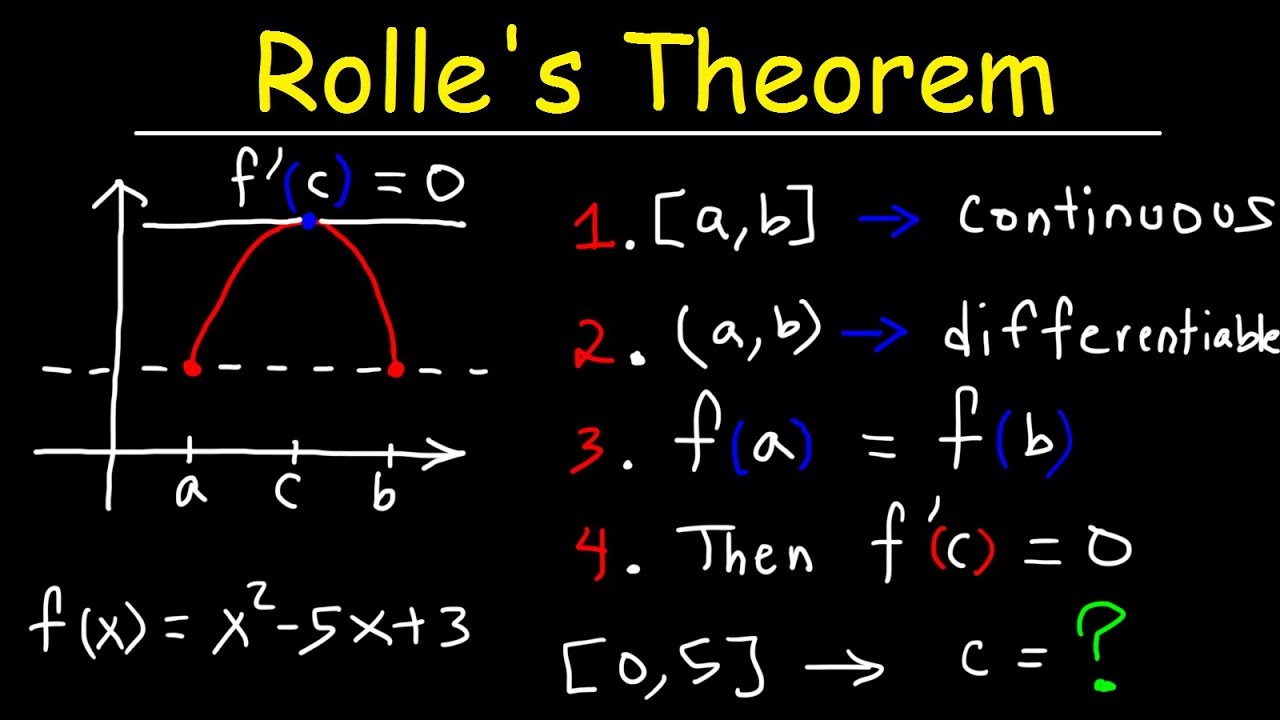
📝 The Rolle's Theorem (RSTM) states that if a function F is continuous on a closed interval [a, b] and differentiable on the open interval (a, b) with F(a) = F(b), then there exists at least one c in (a, b) such that F'(c) = 0.
📈 To apply RSTM, verify the function's continuity and differentiability on the given interval, and check if the function values at the endpoints are equal.
🔍 When working with polynomial functions, they are generally continuous and differentiable across their domain, with no issues arising from discontinuities.
🌀 For rational functions, be cautious of points where the denominator is zero, as these can cause discontinuities and affect the applicability of theorems like RSTM.
🛠️ When finding the value of c in RSTM, first calculate the derivative of the function, then set it equal to zero and solve for c, ensuring that c lies within the interval (a, b).
📊 The Mean Value Theorem (MVT) extends RSTM, stating that for a continuous function on a closed interval [a, b] and differentiable on the open interval (a, b), there exists a c such that the slope of the tangent line at c is equal to the slope of the secant line between (a, F(a)) and (b, F(b)).
🔢 The slope of the secant line is calculated as the change in y divided by the change in x, which is the ratio of the function values at the interval endpoints.
🌟 RSTM and MVT are powerful tools in calculus for understanding the behavior of functions, particularly in relation to their extrema and the existence of critical points.
📚 When solving problems involving RSTM and MVT, always verify all conditions before proceeding, as failure to meet the criteria can lead to incorrect conclusions.
🧠 Understanding the geometric interpretation of these theorems is crucial; the theorems relate the behavior of a function's graph (tangent and secant lines) to its derivatives.
📈📊 The theorems can be applied to a variety of functions, including polynomial, rational, and radical functions, but always be mindful of their domain and any restrictions that may impact their continuity and differentiability.

Q & A

What does RSTM stand for and what are the conditions for it to apply?
-RSTM stands for Rolle's Theorem. The conditions for it to apply are that the function F must be continuous on a closed interval [a, b] and differentiable on the open interval (a, b), with F(a) being equal to F(b).
What does it mean for a function to be differentiable on an interval?
-A function is differentiable on an interval if it has a derivative at every point within that interval, meaning the slope of the tangent line can be calculated for any point in the interval.
What is the significance of a function having the same y-value at the endpoints of an interval according to Rolle's Theorem?
-If a function has the same y-value at the endpoints of an interval, then according to Rolle's Theorem, there must exist at least one point c in the open interval (a, b) where the derivative of the function (the slope of the tangent line) is equal to zero.
How can you determine if a polynomial function is continuous on a given interval?
-A polynomial function is continuous on a given interval if there are no restrictions on its domain, meaning there are no points of discontinuity such as fractions with zero in the denominator, square root functions with negative inside, or natural log functions with zero or negative numbers.
What is the Mean Value Theorem and how does it relate to Rolle's Theorem?
-The Mean Value Theorem states that if a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one point c in the open interval (a, b) where the derivative of the function at c (the slope of the tangent line) is equal to the slope of the secant line between the points [a, b]. Rolle's Theorem is a special case of the Mean Value Theorem where F(a) = F(b).
What is the role of the first derivative in applying Rolle's Theorem?
-The first derivative of the function is used to find the value of c in the open interval (a, b) where the derivative is equal to zero, indicating a horizontal tangent line and a potential point of local minimum or maximum.
How does the video script demonstrate the application of Rolle's Theorem to the function f(x) = x^2 - 3x + 2 on the interval [0, 3]?
-The script verifies that f(x) = x^2 - 3x + 2 is continuous and differentiable on the interval [0, 3] and that f(0) = f(3). It then finds the first derivative, sets it equal to zero, and solves for c, which results in c = 3/2 being the value where the function has a horizontal tangent line.
Why does the video script conclude that Rolle's Theorem does not apply to the function f(x) = x / (x - 3) on the interval [1, 5]?
-The script concludes that Rolle's Theorem does not apply because the function f(x) = x / (x - 3) is not continuous on the closed interval [1, 5] due to a point of discontinuity at x = 3, where the denominator becomes zero, leading to an undefined value.
How does the video script apply the Mean Value Theorem to the function f(x) = x^2 + 4x + 5 on the closed interval [0, 4]?
-The script applies the Mean Value Theorem by verifying that f(x) = x^2 + 4x + 5 is continuous on the closed interval [0, 4] and differentiable on the open interval (0, 4). It then finds the first derivative, applies the theorem's formula to equate the derivative at c to the slope of the secant line, and solves for c, resulting in c = 2 being the value where the slope of the tangent line equals the slope of the secant line.
What is the main difference between the conditions required for the application of Rolle's Theorem and the Mean Value Theorem?
-The main difference is that Rolle's Theorem requires the function to have the same y-value at the endpoints of the interval (F(a) = F(b)), whereas the Mean Value Theorem does not require this condition; it only needs the function to be continuous on the closed interval [a, b] and differentiable on the open interval (a, b).
How does the video script handle the function f(x) = √(4 - x) on the closed interval [0, 4]?
-The script determines that the function f(x) = √(4 - x) is continuous on the closed interval [0, 4] because the square root function is defined for all x in the interval, including x = 4. However, it notes that the function is differentiable on the open interval (0, 4) but not on the closed interval because the derivative is undefined at x = 4.
What is the conclusion for the value of c in the function f(x) = x / (x + 3) on the closed interval [-1, 3] according to the video script?
-The script concludes that the value of c in the function f(x) = x / (x + 3) on the closed interval [-1, 3] is c = 4/3, as this is the value within the interval where the slope of the tangent line equals the slope of the secant line, according to the Mean Value Theorem.

Outlines

00:00

📚 Introduction to Rolle's Theorem and Mean Value Theorem

This paragraph introduces the concepts of Rolle's Theorem (RSTM) and the Mean Value Theorem. RSTM states that if a function F is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), and F(a) = F(b), then there exists a number c in the interval (a, b) such that F'(c) = 0. The explanation includes a graphical interpretation of the theorem, where the y-values of points a and b are the same, indicating a horizontal tangent line at some point c between them. The paragraph also discusses how to apply this theorem to a given function and verify its conditions.

05:00

🧐 Application of Rolle's Theorem to Specific Functions

This paragraph delves into the application of Rolle's Theorem to specific functions. It begins by examining a polynomial function f(x) = x^2 - 3x + 2 on the closed interval [0, 3]. The function satisfies the conditions of RSTM, and the paragraph demonstrates how to find the value of c that makes F'(c) = 0. The explanation continues with examples of functions that do not meet the criteria for RSTM, such as a rational function with a point of discontinuity at x = 3, and a polynomial function that does meet the criteria but has multiple c values within the interval.

10:02

🔍 Further Exploration of Rolle's Theorem and Differentiability

This paragraph continues the exploration of Rolle's Theorem, focusing on the differentiability of functions. It examines a function f(x) = x * √(4 - x) on the closed interval [0, 4], discussing the continuity and differentiability of the function within this interval. The paragraph clarifies that while the function is continuous on the closed interval, it is not differentiable at x = 4, which is a point of discontinuity in the derivative. The explanation emphasizes the importance of differentiability for the application of RSTM.

15:02

📈 Mean Value Theorem and Graphical Analysis

The Mean Value Theorem is introduced in this paragraph, which states that if a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there exists a point c in the interval (a, b) where the slope of the tangent line (f'(c)) is equal to the slope of the secant line (F(b) - F(a) / (b - a)). The paragraph provides a graphical interpretation of the theorem, explaining the concepts of tangent and secant lines and their relationship to the slope. It also presents a problem involving a quadratic function f(x) = x^2 + 4x + 5 on the interval [0, 4], demonstrating how to find the value of c that satisfies the conclusion of the Mean Value Theorem.

20:06

🤔 Analysis of Continuous and Differentiable Functions

This paragraph analyzes the conditions for a function to be continuous and differentiable on a given interval. It examines a rational function f(x) = x / (x + 3) on the closed interval [-1, 3]. The function is continuous on this interval except at x = -3, where the function is undefined due to division by zero. The paragraph then discusses the derivative of the function and its continuity, noting that the function is differentiable on the open interval (-1, 3) but not on the closed interval [-1, 3]. The explanation includes the application of the Mean Value Theorem to find the value of c that makes the slopes of the tangent and secant lines equal.

25:09

🌟 Solving for Tangent and Secant Line Slopes

The final paragraph focuses on solving for the values of c that make the slopes of the tangent and secant lines equal. It presents a problem with the function f(x) = x / (x + 3) on the closed interval [-1, 3] and shows how to apply the Mean Value Theorem to find the specific value of c. The paragraph details the process of setting the derivative equal to the ratio of the function values at the endpoints of the interval, solving for c, and verifying that the found value is within the interval. The explanation includes the mathematical steps and the final result, which is a positive value for c that satisfies the theorem's conditions.

Mindmap

Keywords

💡Rolle's Theorem

Rolle's Theorem is a fundamental concept in calculus that states if a function is continuous on a closed interval [a, b], differentiable on the open interval (a, b), and its values at the endpoints of the interval are equal (f(a) = f(b)), then there exists at least one c in the open interval (a, b) where the first derivative of the function (f'(c)) is zero. This theorem is used to find horizontal tangents or to prove that a function has a point where the slope is zero. The video uses graphs to illustrate instances where Rolle's Theorem applies, such as a function that starts and ends at the same y-value, indicating the existence of at least one point where the slope of the tangent line is zero.

💡Differentiable

Differentiability refers to a property of a function where it has a derivative at each point in its domain. For a function to be differentiable on an interval, it must not have any points of discontinuity, sharp points, or vertical tangent lines within that interval. The video emphasizes the importance of differentiability in the context of Rolle's Theorem and the Mean Value Theorem, explaining that for these theorems to apply, the function must be differentiable on the open interval (a, b). Examples are provided to clarify that polynomial functions are differentiable everywhere, unlike some functions with fractions, square roots, or logarithms that might have restrictions.

💡Continuous

Continuity in the context of the video is described as a characteristic of functions where they do not have any breaks, jumps, or points of discontinuity in their domain. For Rolle's Theorem and the Mean Value Theorem to apply, a function must be continuous on a closed interval [a, b]. The script details that polynomial functions are continuous everywhere, which qualifies them for analysis under these theorems. Continuity ensures that the function’s graph can be drawn without lifting the pencil from the paper, symbolizing a constant connection of points within the interval.

💡Closed Interval

A closed interval, denoted as [a, b], includes the endpoints a and b along with all the points between them. In the context of the video, Rolle's Theorem and the Mean Value Theorem require the function to be continuous on a closed interval. This ensures that the endpoints of the interval are considered in the analysis, which is crucial for the application of these theorems, as they both involve conditions that include the values of the function at these endpoints.

💡Mean Value Theorem

The Mean Value Theorem is a key concept in calculus that builds upon the foundation of Rolle's Theorem. It states that if a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one c in (a, b) such that the derivative of the function at c is equal to the average rate of change of the function over [a, b]. The video explains this by illustrating that the slope of the tangent line at this point c is the same as the slope of the secant line connecting the start and end points of the function on the interval, emphasizing the theorem's utility in connecting differential and average changes.

💡Polynomial Functions

Polynomial functions are expressed as sums of terms consisting of a variable raised to a non-negative integer power, multiplied by a coefficient. The video highlights polynomial functions for their continuity and differentiability across their entire domain, making them prime examples for the application of Rolle's Theorem and the Mean Value Theorem. Through examples, the video illustrates how polynomial functions, due to their nature, do not possess points of discontinuity or non-differentiability under standard conditions, thus often satisfying the prerequisites of these theorems.

💡Derivative

The derivative of a function at a point represents the rate at which the function's value changes at that point, often visualized as the slope of the tangent line to the function's graph at the point. The video frequently discusses derivatives in the context of finding points where the derivative equals zero (horizontal tangents) as stipulated by Rolle's Theorem, or in calculating the specific value required by the Mean Value Theorem to demonstrate the slope of the tangent line equals the slope of the secant line over an interval.

💡Tangent Line

A tangent line to a curve at a given point is a straight line that touches the curve at that point without crossing it. The slope of the tangent line at a point is equal to the derivative of the function at that point. In the video, the concept of tangent lines is crucial for visualizing and understanding the geometric implications of Rolle's Theorem and the Mean Value Theorem, where the existence of a point with a horizontal tangent line (slope of zero) or a point where the tangent line's slope matches the secant line's slope is demonstrated.

💡Secant Line

A secant line is a line that intersects two points on a curve. In the context of the Mean Value Theorem as discussed in the video, the secant line connects the endpoints of the function over a closed interval [a, b]. The theorem posits that there exists at least one point within this interval where the slope of the tangent line to the curve equals the slope of this secant line, emphasizing a fundamental connection between average rates of change (secant slope) and instantaneous rates of change (tangent slope).

💡Horizontal Tangents

Horizontal tangents refer to tangent lines to the graph of a function that are parallel to the x-axis, indicating that the derivative of the function at those points is zero. The concept of horizontal tangents is central to the explanation of Rolle's Theorem in the video, where the theorem's conditions guarantee the existence of at least one point within a specific interval where the function exhibits a horizontal tangent, thereby illustrating a stationary point or a point of inflection on the function's graph.

Highlights

Introduction to Rolle's Theorem (R STM) and its conditions for applicability.

Explanation of the necessity for a function to be continuous and differentiable on a given interval for R STM to apply.

Illustration of the concept using a graphical representation of a function where the y-value of points a and b are the same.

Application of R STM to a polynomial function, emphasizing its continuity and differentiability on a closed interval.

Verification of the conditions for R STM and calculation of the value of c where the derivative is zero for the function f(x) = x^2 - 3x + 2.

Discussion on the discontinuity in a rational function and how it affects the applicability of Rolle's Theorem.

Demonstration of the application of R STM to a cubic function and the process of finding the value of c where the derivative equals zero.

Explanation of the Mean Value Theorem and its difference from Rolle's Theorem in terms of the slope of the tangent and secant lines.

Application of the Mean Value Theorem to a quadratic function and the derivation of the value of c where the slopes of the tangent and secant lines are equal.

Analysis of the domain restrictions for a function involving a square root and its continuity on a closed interval.

Process of finding the derivative of a function involving a square root and the determination of the c value where the derivative is zero.

Graphical analysis of a function and the identification of the c value where the slope of the tangent line is zero.

Revisiting the conditions of Rolle's Theorem and the importance of the function being differentiable on the open interval.

Application of Rolle's Theorem to a rational function and the calculation of the c value where the derivative is undefined.

Explanation of the quotient rule for finding the derivative of a rational function and its application to a specific problem.

Solution of a problem using the Mean Value Theorem for a rational function and the determination of the c value where the slopes are equal.

Conclusion of the transcript with a summary of the problem-solving process and the application of both Rolle's and Mean Value Theorems.

Transcripts

Browse More Related Video

Calculus 1 Lecture 3.2: A BRIEF Discussion of Rolle's Theorem and Mean-Value Theorem.

The MEAN Value Theorem is Actually Very Nice

Mean Value Theorem

Calculus AB Homework 5.1 Rolle's and Mean Value Theorem

Mean Value Theorem and Rolle's Theorem

Rolle's Theorem

Related Tags

Rolle's Theorem Mean Value Theorem Mathematics Derivatives Continuous Functions Differentiable Functions Polynomial Functions Rational Functions Quadratic Functions Math Tutorial