Calculus AB Homework 5.1 Rolle's and Mean Value Theorem

Michelle Krummel

24 Jan 201833:52

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script guides viewers through applying Rolle's Theorem and the Mean Value Theorem to various functions. It explains the necessary conditions for the theorems' applicability, including continuity on a closed interval and differentiability on an open interval. The script provides step-by-step solutions for finding values of 'C' where the derivative equals zero or the average rate of change, using polynomial, trigonometric, and rational functions as examples. It also discusses situations where these theorems do not apply due to discontinuities or non-differentiability.

Takeaways

📚 The video is a tutorial on applying Rolle's Theorem to determine if it can be used for given functions on specific intervals and to find the values of C that satisfy the theorem's conditions.
🔍 To apply Rolle's Theorem, three conditions must be met: the function must be continuous on a closed interval, differentiable on the open interval, and the function values must be equal at the endpoints.
📉 The script provides step-by-step examples of applying the theorem to polynomial functions, which are inherently continuous and differentiable everywhere, simplifying the verification process.
📝 For non-polynomial functions, the script suggests visualizing the graph to determine continuity and differentiability, which is crucial for verifying the conditions of Rolle's Theorem.
📌 The video demonstrates solving for the value of C by taking the derivative of the function and setting it equal to zero, which is a key step in applying Rolle's Theorem.
📈 The Mean Value Theorem is introduced as a more general principle that guarantees the existence of a point where the derivative equals the average rate of change, without requiring the derivative to be zero.
📊 The script explains that the Mean Value Theorem requires only continuity on the closed interval and differentiability on the open interval, without the need for endpoint function values to be equal.
🚫 The video uses examples to show when Rolle's Theorem cannot be applied, such as when a function is not continuous or differentiable on the given interval.
📐 The script includes examples of rational functions and trigonometric functions, highlighting the importance of understanding their properties to apply the theorems correctly.
📘 The tutorial emphasizes the importance of checking the function's behavior at endpoints and within intervals, especially when the function is not a polynomial, to ensure the theorems' conditions are met.
📝 The final examples illustrate how to determine if Rolle's Theorem or the Mean Value Theorem can be applied by analyzing the function's graph and properties within the given intervals.

Q & A

What are the conditions required for Rolle's Theorem to apply to a function on a given interval?
-Rolle's Theorem applies if the function is continuous on the closed interval, differentiable on the open interval, and the function values are equal at the endpoints of the interval.
Why are polynomial functions easy to work with when checking for Rolle's Theorem conditions?
-Polynomial functions are continuous and differentiable everywhere for all real numbers, which means they automatically satisfy the first two conditions of Rolle's Theorem.
What is the derivative of the function f(x) = x^2 - 4x used to find in the script?
-The derivative f'(x) = 2x - 4 is used to find the value of x where the derivative equals zero, which is a requirement of Rolle's Theorem.
What is the value of C found in the script for the function f(x) = x + 4(x - 3)^2 when applying Rolle's Theorem?
-The value of C found is 2/3, which is the point where the derivative of the function equals zero and lies within the interval (-4, 3).
Why does the script mention that the function f(x) = 4 - |x - 2| does not satisfy the conditions for Rolle's Theorem on the interval (-3, 7)?
-The function is not differentiable at x = 2, which is within the interval (-3, 7), thus failing to meet one of the conditions required for Rolle's Theorem.
What is the significance of the endpoints' function values being equal in Rolle's Theorem?
-The equal function values at the endpoints ensure that there is a possibility for the function to have a derivative equal to zero within the interval, which is the main conclusion of Rolle's Theorem.
How does the script use the Mean Value Theorem differently from Rolle's Theorem?
-The Mean Value Theorem requires the function to be continuous on the closed interval and differentiable on the open interval, but it does not require the function values to be equal at the endpoints. It guarantees that the derivative will equal the average rate of change over the interval, not necessarily zero.
What is the average rate of change for the function f(x) = x^3 - x^2 - 2x on the interval (-1, 1) according to the script?
-The average rate of change is calculated as f(1) - f(-1) divided by the difference in the interval, which results in -1 for this function on the given interval.
Why is the function f(x) = sqrt(x - 3) not differentiable at x = 3?
-The function is not differentiable at x = 3 because the square root function has a domain restriction, and the derivative would involve division by zero at this point.
What is the solution for x when the derivative of the function f(x) = x + 2/x is set equal to the average rate of change on the interval (1/2, 2)?
-The solution for x is found to be 1, after setting the derivative equal to the average rate of change and solving the resulting equation.
How does the script determine the applicability of Rolle's Theorem or the Mean Value Theorem for the function f(x) on the interval (-5, -1)?
-The script determines that neither Rolle's Theorem nor the Mean Value Theorem can be applied because the function is not continuous or differentiable on the interval due to a discontinuity at x = -3.

Outlines

00:00

📚 Application of Rolle's Theorem to Polynomial Functions

The paragraph discusses the application of Rolle's Theorem to a polynomial function on the interval [0, 4]. It explains the three conditions necessary for Rolle's Theorem to apply: continuity on the closed interval, differentiability on the open interval, and equality of function values at endpoints. The function f(x) = x^2 - 4x is analyzed, and it is found to meet all conditions, leading to the conclusion that there exists a point C where the derivative f'(x) = 2x - 4 equals zero, which is solved to be C = 2.

05:01

🔍 Rolle's Theorem Application with a Quadratic Function

This paragraph examines the use of Rolle's Theorem for the function f(x) = x + 4x^2 - 3 on the interval [-4, 3]. It confirms the function's continuity and differentiability on the given interval and checks the function values at the endpoints, finding them equal. The derivative f'(x) = 2x + 4 is factored to find the points where it equals zero, yielding solutions x = -4 and x = 2/3. The interval-specific solution C = 2/3 is selected as the value satisfying Rolle's Theorem.

10:03

🚫 Failure to Apply Rolle's Theorem Due to Non-Differentiability

The paragraph addresses the function f(x) = 4 - |x - 2| on the interval [-3, 7] and determines that Rolle's Theorem cannot be applied. Although the function is continuous, the presence of a corner point at x = 2 means it is not differentiable on the interval, thus failing to meet one of the necessary conditions for Rolle's Theorem. The graph of the function is visualized to illustrate this, showing the non-differentiability at x = 2.

15:04

🌀 Applying Rolle's Theorem to Sine Function

The paragraph applies Rolle's Theorem to the sine function f(x) = sin(x) on the interval [0, 2π]. It confirms the sine function's continuity and differentiability on the interval and checks the function values at the endpoints, both equal to zero. The derivative f'(x) = cos(x) is set to zero to find the points where the derivative equals zero, yielding solutions x = π/2 and x = 3π/2, both within the interval, thus satisfying Rolle's Theorem.

20:05

📉 Mean Value Theorem Application to Polynomial Functions

The paragraph discusses the Mean Value Theorem's application to the function f(x) = x^3 - x^2 - 2x, which is a polynomial and thus continuous and differentiable everywhere. The theorem's conditions are met, and the derivative f'(x) = 3x^2 - 2x - 2 is found. The average rate of change over the interval [-1, 1] is calculated and set equal to the derivative to find the point C = -1/3 where the derivative equals the average rate of change.

25:08

📈 Mean Value Theorem for a Square Root Function

The paragraph examines the function f(x) = √(x - 3) on the interval [3, 7], confirming its continuity and differentiability on the interval, except at the endpoint x = 3. The derivative f'(x) = 1/(2√(x - 3)) is found, and the average rate of change is calculated. The equation is solved to find the point C = 4 where the derivative equals the average rate of change, verifying the Mean Value Theorem's application.

30:09

🔢 Mean Value Theorem for a Rational Function

The paragraph discusses the function f(x) = (x + 2)/x on the interval [1/2, 2]. It confirms the function's continuity and differentiability on the interval, except at x = 0, which is not part of the interval. The derivative f'(x) = -2/x^2 is found, and the average rate of change is calculated. The equation is solved to find the point C = 1 where the derivative equals the average rate of change, applying the Mean Value Theorem.

📊 Mean Value Theorem for Trigonometric Functions

The paragraph applies the Mean Value Theorem to the function H(x) = 2cos(x) + cos(2x) on the interval [0, π]. The function's continuity and differentiability on the interval are confirmed, and the derivative H'(x) = -2sin(x) - 2sin(2x) is found. The average rate of change is calculated, and the equation is solved graphically to find the points C ≈ 0.217 and C ≈ 1.748 where the derivative equals the average rate of change, both within the interval.

🚫 Inapplicability of Rolle's and Mean Value Theorems

The final paragraph assesses the applicability of Rolle's and Mean Value Theorems to various functions on different intervals. It determines that for the interval [-5, -1], Rolle's Theorem cannot be applied due to discontinuity and non-differentiability at x = -3. For the interval [-2, 8], Rolle's Theorem is not applicable due to non-differentiability at x = -1. However, the Mean Value Theorem applies to the interval [-1, 8] as the function is continuous and differentiable on the open interval, satisfying the necessary conditions.

Mindmap

Keywords

💡Rolle's Theorem

Rolle's Theorem is a fundamental concept in calculus that states if a function is continuous on a closed interval and differentiable on the open interval within that, and the function values are equal at the endpoints, then there is at least one point in the interval where the derivative of the function is zero. In the video, Rolle's Theorem is applied to various functions to determine if the conditions are met, and if so, to find the value(s) of 'C' where the derivative equals zero.

💡Differentiable

A function is 'differentiable' at a point if it has a derivative at that point, meaning the function's rate of change can be calculated. In the context of the video, differentiability is one of the key conditions checked for applying Rolle's Theorem, as the function must be differentiable on the open interval between the endpoints where the function values are equal.

💡Continuous

Continuity in a function means that the function does not have any breaks or jumps in its graph; it is unbroken and can be drawn without lifting the pen. The video script emphasizes the importance of a function being continuous on a closed interval as a prerequisite for applying Rolle's Theorem.

💡Polynomial Function

A 'polynomial function' is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The script mentions polynomial functions as examples of functions that are both continuous and differentiable everywhere, making them suitable for Rolle's Theorem applications.

💡Derivative

The 'derivative' of a function measures the rate at which the function's output (or value) changes with respect to changes in its input. In the video, finding the derivative of a function is a step towards applying Rolle's Theorem, as the theorem seeks the point(s) where this derivative is zero.

💡Mean Value Theorem

The 'Mean Value Theorem' is a generalization of Rolle's Theorem and states that if a function is continuous on a closed interval and differentiable on the open interval, then there exists a point 'C' where the derivative of the function equals the average rate of change of the function over that interval. The script contrasts Rolle's Theorem with the Mean Value Theorem, explaining that the latter does not require the derivative to be zero but rather equal to the average rate of change.

💡Average Rate of Change

The 'average rate of change' of a function over an interval is the difference in the function values at the endpoints of the interval divided by the difference in the input values. In the context of the Mean Value Theorem discussed in the video, the average rate of change is compared to the derivative to find the point where they are equal.

💡Trigonometric Function

A 'trigonometric function' is a function of an angle, involving sine, cosine, and other related functions. The video script mentions trigonometric functions as examples of functions that are continuous and differentiable everywhere, which is why they can be considered for the application of Rolle's Theorem.

💡Absolute Value Function

The 'absolute value function' is a mathematical function that takes a number and returns its non-negative magnitude, effectively reflecting the graph across the x-axis at the origin. The script uses the absolute value function to illustrate a case where a function is not differentiable at certain points, hence not satisfying the conditions for Rolle's Theorem.

💡Endpoint

An 'endpoint' in the context of an interval refers to the starting or ending value of that interval. The script discusses the importance of the function having equal values at the endpoints for Rolle's Theorem to apply and checks these endpoint values for various functions to determine if the theorem can be applied.

💡Discontinuity

A 'discontinuity' in a function occurs where the function is not defined or the limit exists but is not the same as the function's value at that point. The video script uses the concept of discontinuity to explain why certain functions do not meet the criteria for applying Rolle's Theorem, as they are not continuous over the specified interval.

Highlights

Introduction to applying Rolle's Theorem to determine the existence of a point where the derivative of a function equals zero within a given interval.

Necessity of checking three conditions for Rolle's Theorem: continuity on a closed interval, differentiability on an open interval, and equality of function values at endpoints.

Polynomial functions are inherently continuous and differentiable everywhere, simplifying the application of Rolle's Theorem.

Verification of function values at endpoints to ensure they are equal, a requirement for Rolle's Theorem.

Derivation of a specific function and solving for when the derivative equals zero to find the value of C.

Application of the product rule in finding the derivative of a function involving a squared term multiplied by a linear term.

Factoring techniques to simplify derivatives and solve for critical points where the derivative equals zero.

Discussion on the limitations of Rolle's Theorem when a function is not differentiable at a point within the interval.

Visualization of function graphs to determine continuity and differentiability, particularly for non-polynomial functions.

Application of the Mean Value Theorem as a generalization of Rolle's Theorem, requiring fewer conditions.

Use of the quotient rule for derivatives of rational functions and solving for where the derivative equals the average rate of change.

Graphical interpretation of the Mean Value Theorem to find the interval where the derivative equals the average rate of change.

Analysis of trigonometric functions and their properties of continuity and differentiability for theorem application.

Solution of derivative equations for trigonometric functions to find points where the sine equals zero.

Determination of the interval for which the Mean Value Theorem applies, based on the function's continuity and differentiability.

Identification of discontinuities and non-differentiability in functions to ascertain the inapplicability of Rolle's Theorem.

Final review of the conditions required for the Mean Value Theorem and verification of their satisfaction for a given function.

Transcripts

Browse More Related Video

Calculus 1: Lecture 3.2 Rolle's Theorem and the Mean Value Theorem

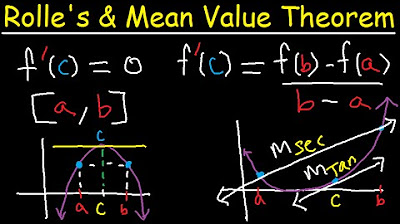
Rolle's Theorem Explained and Mean Value Theorem For Derivatives - Examples - Calculus

Mean Value Theorem and Rolle's Theorem

Using IVT, MVT, and EVT

Calculus 1 Lecture 3.2: A BRIEF Discussion of Rolle's Theorem and Mean-Value Theorem.

Mean Value Theorem

Related Tags

Rolle's Theorem Mean Value Theorem Calculus Problems Polynomial Functions Trigonometric Functions Derivative Applications Continuous Functions Differentiable Functions Mathematical Analysis Educational Content