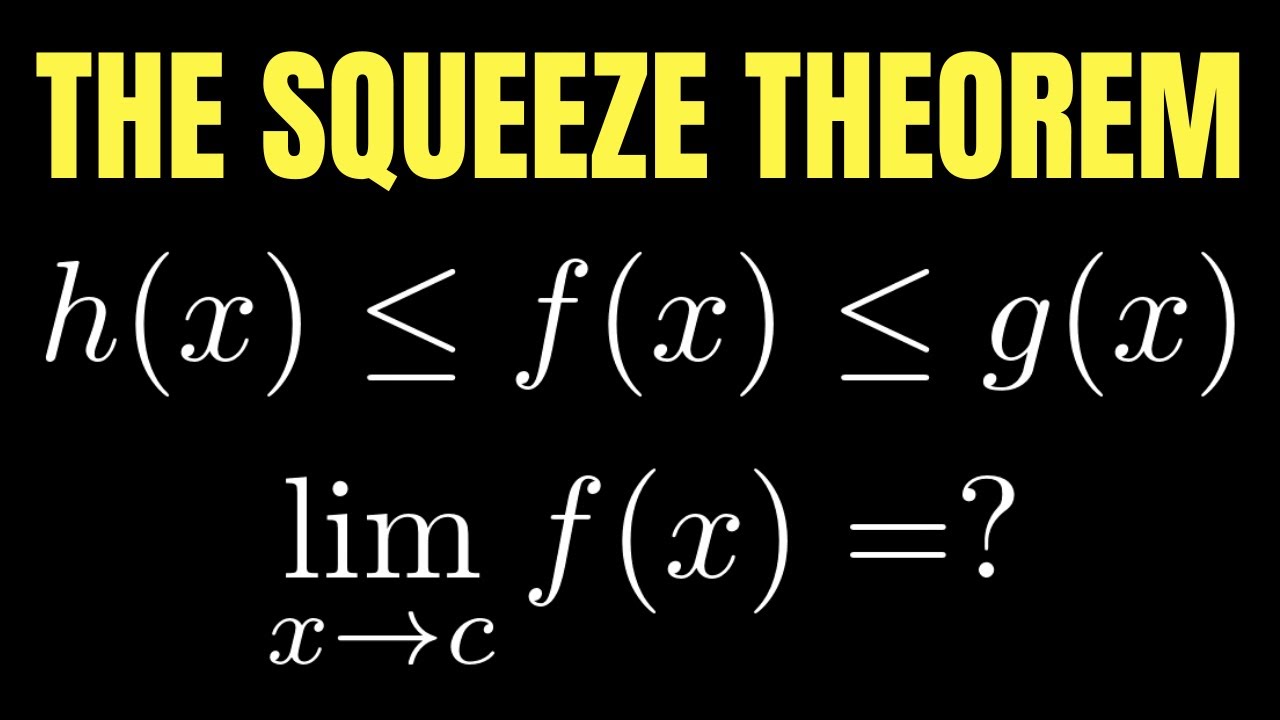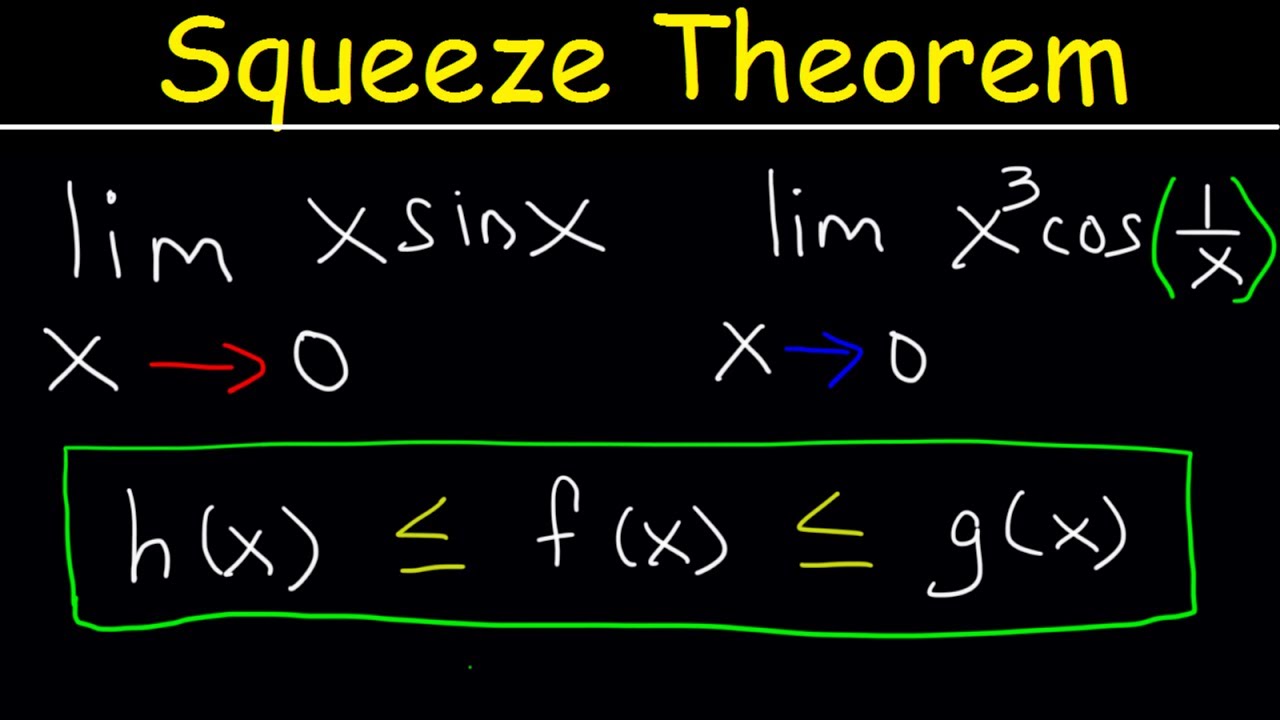The Squeeze Theorem for Limits, Example 1
TLDRThis video script introduces the Squeeze Theorem, a concept in calculus dealing with limits. The theorem states that if a function H(x) is trapped between two other functions f(x) and G(x), and both lim_{x o a} f(x) and lim_{x o a} G(x) equal a certain value L, then lim_{x o a} H(x) must also equal L. The script illustrates the theorem with two examples: one involving a straightforward application to find the limit of a function f(x) bounded by 3x and x^3 + 2 as x approaches 1, and another where the limit of x^2 * cos(1/x^2) as x approaches 0 is determined by bounding the cosine function between -1 and 1. The video aims to clarify the application of the theorem and offers assistance for further questions.
Takeaways
- 📚 The Squeeze Theorem is a mathematical concept used to find limits of functions.
- 📈 The theorem involves comparing a function 'f(x)' to two other functions 'G(x)' and 'H(x)' where 'f(x)' is greater than or equal to 'G(x)' and less than or equal to 'H(x)'.
- 🔍 If the limits of 'G(x)' and 'H(x)' as 'x' approaches 'a' are equal, then the limit of 'f(x)' as 'x' approaches 'a' is also that value.
- 🤔 The challenge often lies in identifying the outer functions 'G(x)' and 'H(x)' that can be used to 'squeeze' the middle function.
- 🔢 An example provided is where 'f(x)' is bounded by '3x' and 'x^3 + 2', and the limit as 'x' approaches 1 of 'f(x)' is found to be 3 using the Squeeze Theorem.
- 🚫 The Squeeze Theorem is particularly useful when direct substitution into the function results in an undefined expression.
- 🌟 The example of 'x^2 * cos(1/x^2)' as 'x' approaches 0 demonstrates how to apply the Squeeze Theorem when direct substitution is not possible.
- 📉 In the 'x^2 * cos(1/x^2)' example, the function is bounded by 'x^2' and '-x^2', and the limit is found to be 0.
- 🧩 The process involves identifying the bounds and then using the Squeeze Theorem to determine the limit of the function of interest.
- 📝 The script suggests that sometimes the trick is to use the properties of trigonometric functions, like the range of cosine, to establish the bounds.
- 💌 The video offers help for further questions via email, emphasizing a willingness to assist with additional queries.
Q & A
What is the Squeeze Theorem?
-The Squeeze Theorem is a mathematical principle used to find the limit of a function when direct substitution into the function yields an indeterminate form. It states that if two functions 'f(x)' and 'g(x)' converge to the same limit 'L' as 'x' approaches 'a', and another function 'h(x)' is trapped between 'f(x)' and 'g(x)', then the limit of 'h(x)' as 'x' approaches 'a' is also 'L'.
How does the Squeeze Theorem relate to limits?
-The Squeeze Theorem is specifically used to evaluate limits. It helps determine the limit of a function when direct substitution results in an undefined or indeterminate form, by 'squeezing' the function of interest between two other functions whose limits are known.
What is the condition for the Squeeze Theorem to be applicable?
-The Squeeze Theorem can be applied when there exists a function 'h(x)' that is greater than or equal to 'g(x)' and less than or equal to 'f(x)' for all 'x' in a certain interval around 'a', and both 'f(x)' and 'g(x)' have the same limit 'L' as 'x' approaches 'a'.
Can you explain the first example given in the transcript using the Squeeze Theorem?
-In the first example, the function 'f(x)' is bounded between '3x' and 'x^3 + 2' for all 'x' between 0 and 2. The limit as 'x' approaches 1 of both '3x' and 'x^3 + 2' is 3. Since 'f(x)' is squeezed between these two functions, by the Squeeze Theorem, the limit of 'f(x)' as 'x' approaches 1 is also 3.
What is the significance of the second example in the transcript?
-The second example demonstrates how to use the Squeeze Theorem when dealing with a function that involves an indeterminate form, such as '0/0'. Here, 'x^2 * cos(1/x^2)' as 'x' approaches 0 is bounded by '-x^2' and 'x^2'. Since both bounds approach 0, the Squeeze Theorem implies that the limit of the function is also 0.
Why can't we directly substitute 'x = 0' in the second example?
-Direct substitution of 'x = 0' in the second example results in an undefined expression because 'cos(1/0)' is not defined. Hence, the Squeeze Theorem is used to find the limit by bounding the function with known limits.
What is a common trick mentioned in the transcript for using the Squeeze Theorem with trigonometric functions?
-A common trick mentioned is to use the fact that the cosine function is always between -1 and 1. By multiplying the inside of the cosine function by 'x^2', the resulting expression is bounded between '-x^2' and 'x^2', which can be used to apply the Squeeze Theorem.
How does the Squeeze Theorem help in situations where direct calculation of a limit is not possible?
-The Squeeze Theorem helps by allowing the evaluation of a limit through the limits of simpler functions that 'squeeze' the function of interest. This is particularly useful when direct substitution leads to an indeterminate form, such as 0/0 or infinity/infinity.
What is the role of the function 'h(x)' in the context of the Squeeze Theorem?
-In the context of the Squeeze Theorem, 'h(x)' is the function whose limit is being sought. It must be greater than or equal to 'g(x)' and less than or equal to 'f(x)', and as 'x' approaches 'a', both 'f(x)' and 'g(x)' converge to the same limit 'L', thus implying that 'h(x)' also converges to 'L'.
Can the Squeeze Theorem be applied to functions that are not continuous?
-The Squeeze Theorem can be applied to any function that can be bounded between two other functions, regardless of their continuity. The key is that the bounding functions must have the same limit as 'x' approaches 'a'.
What is the main challenge when applying the Squeeze Theorem?
-The main challenge is often identifying or creating the bounding functions 'f(x)' and 'g(x)' that have known limits and can effectively 'squeeze' the function 'h(x)' of interest. This requires a good understanding of the behavior of the functions involved.
Outlines
📚 Introduction to the Squeeze Theorem
This paragraph introduces the Squeeze Theorem, a fundamental concept in calculus that deals with limits. The theorem is explained through a graphical representation where a function f(x) is sandwiched between two other functions, G(x) and H(x), at a specific point 'a'. The key takeaway is that if the limits of the outer functions as x approaches 'a' are equal, then the limit of the function in between (H(x)) must also be the same. The explanation is supported by an example where the function f(x) is bounded by 3x and x^3 + 2, and the limit as x approaches 1 is evaluated using the theorem.
🔍 Applying the Squeeze Theorem to a Trigonometric Limit
The second paragraph delves into applying the Squeeze Theorem to evaluate the limit of a function involving a trigonometric expression, x^2 * cos(1/x^2), as x approaches zero. The direct substitution is not possible due to the undefined nature of the cosine function at the point of interest. Instead, the theorem is used to bound the expression between -x^2 and x^2, leveraging the fact that the cosine function always lies between -1 and 1. By recognizing the limits of these bounding functions as x approaches zero, the paragraph concludes that the original function's limit must also be zero, thus demonstrating a practical application of the Squeeze Theorem in a non-obvious scenario.
Mindmap
Keywords
💡Squeeze Theorem
💡Limits
💡Function
💡Intersection
💡Cosine
💡Trigonometric Functions
💡X-coordinate
💡Y-coordinate
💡Cubed
💡Inequality
Highlights
Introduction to the Squeeze Theorem and its application in calculating limits.
The Squeeze Theorem is used when dealing with limits of functions where direct substitution is not possible.
Explanation of how the Squeeze Theorem works with a graphical representation of functions f(x) and g(x).
Condition for the Squeeze Theorem: a function H(x) is trapped between f(x) and g(x).
If the limits of f(x) and g(x) as x approaches a are equal, then H(x) must also have the same limit.
Demonstration of the Squeeze Theorem with an example involving the function f(x) being greater than or equal to 3x and less than or equal to x cubed plus 2.
Calculating the limit as x approaches 1 of f(x) using the limits of 3x and x cubed plus 2, both yielding 3.
Application of the Squeeze Theorem to conclude that the limit of f(x) as x approaches 1 is 3.
Introduction of a second problem involving the limit of x squared times the cosine of one over x squared as x approaches zero.
Explanation of why direct substitution is not possible for the second problem due to the undefined nature of the expression.
Use of the range of the cosine function to establish bounds for x squared times cosine of one over x squared.
Finding the limits of the bounding functions as x approaches zero and applying the Squeeze Theorem to determine the limit of the original function.
Conclusion that the limit of x squared times cosine of one over x squared as x approaches zero is 0.
Emphasis on the importance of identifying bounding functions when using the Squeeze Theorem, especially with trigonometric functions.
Encouragement for viewers to reach out with questions and an offer of assistance via email.
Final summary of the Squeeze Theorem's utility and a reminder of its application in finding limits of functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: