Calculus: The Squeeze Theorem Full Tutorial

The Math Sorcerer
6 May 202210:59
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the Squeeze Theorem, also known as the Pinching Theorem or Sandwich Theorem, which is a fundamental concept in calculus. The theorem is introduced with two conditions: a function f(x) is bounded by two other functions h(x) and g(x) for all x in an interval containing c, except possibly at c itself. If the limits of h(x) and g(x) as x approaches c are equal to a real number l, then the limit of f(x) as x approaches c is also l. The script proceeds to illustrate the theorem with two classic examples involving the sine and cosine functions. The first example calculates the limit as x approaches 0 of x times the sine of 1/x, while the second example deals with the limit as x approaches 0 of x squared times the cosine of 2022/x to the power of 2021. Both examples demonstrate the application of the Squeeze Theorem by showing that the limits of the bounding functions are equal, thereby concluding that the limit of the function in question also equals zero. The explanation is designed to be accessible and engaging for students learning calculus.

Takeaways
  • 📚 The Squeeze Theorem, also known as the Pinching Theorem or Sandwich Theorem, is a mathematical theorem used to find limits of functions.
  • 🤏 The theorem states that if a function f(x) is trapped between two other functions g(x) and h(x), and both g(x) and h(x) approach the same limit L as x approaches c, then f(x) also approaches L.
  • ✅ The first condition for applying the theorem is that h(x) ≤ f(x) ≤ g(x) for all x in an interval containing c, except possibly at c itself.
  • 🔍 The second condition is that the limits of h(x) and g(x) as x approaches c both exist and are equal to L.
  • 🚫 If you plug in the value of c into the function and it results in an undefined expression (like division by zero), the Squeeze Theorem can be a useful tool to find the limit.
  • 📉 A common example used to illustrate the theorem is the limit as x approaches 0 of x times the sine of 1/x.
  • 📈 To apply the theorem, you can use known inequalities such as the range of the sine function, which is between -1 and 1.
  • 💡 Multiply the inequality by x to get the bounds of the function you're interested in, which in the example is x * sin(1/x).
  • 🧮 Take the limit of the bounds as x approaches the value in question (e.g., 0), and if both bounds approach the same limit, apply the Squeeze Theorem to conclude the limit of the function.
  • 📌 The process involves finding a lower bound (h(x)) and an upper bound (g(x)) for the function f(x), then showing that the limits of h(x) and g(x) are the same as x approaches c.
  • 📝 When writing out the solution, it's common to clearly state that by the Squeeze Theorem, the limit of the function f(x) as x approaches c is equal to L.
  • 🔑 Memorizing the structure of the Squeeze Theorem and practicing with various examples can help solidify understanding and make it easier to apply in calculus problems.
Q & A

  • What is the Squeeze Theorem also known as?

    -The Squeeze Theorem is also referred to as the Pinching Theorem and the Sandwich Theorem.

  • What are the two conditions required for the Squeeze Theorem?

    -The two conditions are: 1) h(x) ≤ f(x) ≤ g(x) for all x in some interval containing c, except possibly at c itself, and 2) the limits of h(x) and g(x) as x approaches c both exist and are equal to the same value l.

  • What happens to the function f(x) when it is 'squeezed' between h(x) and g(x)?

    -If f(x) is trapped between h(x) and g(x) and both h(x) and g(x) approach the same limit l as x approaches c, then f(x) must also approach l.

  • Why is the Squeeze Theorem useful when evaluating limits that are indeterminate?

    -The Squeeze Theorem is useful for indeterminate forms because it allows us to find the limit of a function by 'squeezing' it between two other functions whose limits are known and equal.

  • What is the range of the sine function?

    -The range of the sine function is from -1 to 1, inclusive.

  • How is the limit of x * sin(1/x) as x approaches 0 evaluated using the Squeeze Theorem?

    -By using the inequalities -x ≤ x * sin(1/x) ≤ x and taking the limit as x approaches 0, which shows that the limit of x * sin(1/x) is 0.

  • What is the limit of x^2 * cos(2022/x)^2021 as x approaches 0?

    -The limit is 0, as shown by applying the Squeeze Theorem and using the inequalities -x^2 ≤ x^2 * cos(2022/x)^2021 ≤ x^2, with both -x^2 and x^2 approaching 0 as x approaches 0.

  • What is the significance of the Squeeze Theorem in calculus?

    -The Squeeze Theorem is significant in calculus as it provides a method to find limits of functions that may not be directly computable, especially when dealing with indeterminate forms.

  • Why might a student struggle with understanding the Squeeze Theorem?

    -A student might struggle with the Squeeze Theorem if they have difficulty grasping the concept of limits, understanding the inequalities involved, or visualizing how the functions 'squeeze' the middle function towards a limit.

  • What is the key to successfully applying the Squeeze Theorem?

    -The key to successfully applying the Squeeze Theorem is to identify suitable functions h(x) and g(x) that bound the function f(x) and to show that their limits as x approaches c are equal.

  • Can the Squeeze Theorem be used for limits where x does not approach a specific value like 0 or a number?

    -Yes, the Squeeze Theorem can be applied to limits where x approaches any value, including infinity or a specific number other than 0, as long as the conditions of the theorem are met.

  • Why is the Squeeze Theorem particularly useful for evaluating limits involving trigonometric functions?

    -The Squeeze Theorem is particularly useful for evaluating limits involving trigonometric functions because these functions often naturally provide the bounding needed for the theorem, given their well-known ranges and periodicity.

Outlines
00:00
📚 Introduction to the Squeeze Theorem

The Squeeze Theorem, also known as the Pinching or Sandwich Theorem, is introduced with a detailed explanation of its conditions and applications. The theorem is predicated on the existence of three functions, h(x), f(x), and g(x), where f(x) is bounded by h(x) and g(x) within an interval around a point c, except possibly at c itself. If the limits of h(x) and g(x) as x approaches c are equal to a certain value l, and f(x) is 'squeezed' between them, then f(x) also approaches l as x approaches c. An example is given involving the limit of x times the sine of 1/x as x approaches 0, demonstrating how to set up the necessary inequalities and apply the theorem to prove the limit.

05:01
🔍 Applying the Squeeze Theorem with Examples

Further application of the Squeeze Theorem is illustrated through examples, starting with the limit as x approaches 0 of x times the sine of 1/x. The approach involves establishing an inequality using the properties of the sine function and then calculating the limit of the bounding functions as x approaches 0 to demonstrate that they converge to the same value, thus proving that the function of interest does as well. Another example features the limit of x^2 times the cosine of 2022/x to the power of 2021 as x approaches 0, employing a similar strategy by leveraging the properties of the cosine function to establish bounds and apply the theorem.

10:02
🧮 Advanced Example and Summary of the Squeeze Theorem

A continuation of the application of the Squeeze Theorem to more complex functions, focusing on the limit of x^2 times the cosine of 2022/x to the power of 2021 as x approaches 0. This example reinforces the method of applying the theorem by establishing upper and lower bounds using the properties of the cosine function. The summarization underscores the utility and versatility of the Squeeze Theorem in handling limits where direct substitution fails, highlighting it as a fundamental concept in calculus education. The section also touches on the presenter’s personal anecdotes, including technical difficulties encountered during the explanation, adding a human element to the instructional content.

Mindmap
Keywords
💡Squeeze Theorem
The Squeeze Theorem, also known as the Pinching Theorem or Sandwich Theorem, is a fundamental concept in calculus used to find the limit of a function when direct substitution results in an indeterminate form. It states that if a function f(x) is bounded between two other functions h(x) and g(x) for all x in an interval around a certain point c (except possibly at c itself), and the limits of h(x) and g(x) as x approaches c are equal, then the limit of f(x) as x approaches c is also equal to that common limit. In the video, the theorem is applied to solve limits involving trigonometric functions, such as sin(1/x) and cos(2022/x^2021).
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are mathematical functions that describe the relationship between the angles and sides of a triangle. In the context of the video, the sine and cosine functions are used to illustrate the application of the Squeeze Theorem. The video mentions that the range of the sine function is between -1 and 1, which is a key property used to create the necessary inequalities for the Squeeze Theorem.
💡Indeterminate Form
An indeterminate form occurs in calculus when the direct substitution of a variable into an expression results in a value that is undefined or ambiguous, such as 0/0 or ∞/∞. The video script discusses how the Squeeze Theorem can be used to find limits when direct substitution leads to an indeterminate form, such as when evaluating the limit of x * sin(1/x) as x approaches 0.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input (or index) approaches some value. The concept of a limit is central to understanding continuity, derivatives, and integrals. The video focuses on using the Squeeze Theorem to find the limit of certain functions as the variable x approaches a specific value, such as 0.
💡Inequality
An inequality is a mathematical statement that relates expressions that are not necessarily equal, using symbols such as <, >, ≤, or ≥. In the video, inequalities are used to create bounds for the function f(x) in relation to h(x) and g(x), which is essential for applying the Squeeze Theorem. For example, the script mentions that sine of an angle is always less than or equal to 1, which helps establish the upper and lower bounds needed for the theorem.
💡Real Number
A real number is a value that can be found on the continuous number line, which includes all rational and irrational numbers. In the context of the video, the Squeeze Theorem is used to show that the limit of a function, as x approaches a certain point, is a real number. The script emphasizes that if the limits of h(x) and g(x) are equal real numbers as x approaches c, then the limit of f(x) is also that real number.
💡Absolute Value
The absolute value of a number is its distance from zero on the number line, denoted by the symbol | |. It is used to express the magnitude of a number without considering its sign. In the video, the absolute value function is mentioned as an alternative method to create inequalities for the Squeeze Theorem, although it is not explicitly used in the examples provided.
💡Function
A function is a mathematical relationship between two variables, where each value of one variable (the independent variable) uniquely determines a value of the other variable (the dependent variable). In the video, functions f(x), h(x), and g(x) are discussed in the context of the Squeeze Theorem, where f(x) is the function whose limit is being sought, and h(x) and g(x) are functions that bound f(x).
💡Interval
In mathematics, an interval is a set of real numbers with a lower and upper bound. The video script refers to an interval containing a point c, which is the point at which the limit of the function is being evaluated. The Squeeze Theorem applies to functions that satisfy the theorem's conditions for all x within this interval, except possibly at the point c itself.
💡Approaching
In the context of limits, 'approaching' refers to the process of getting arbitrarily close to a particular value or point. The video discusses how, as x approaches a certain value (like 0), the functions h(x) and g(x) approach a common limit l, which implies that the function f(x) also approaches l. This concept is central to the application of the Squeeze Theorem.
💡QED
QED is an abbreviation for the Latin phrase 'quod erat demonstrandum', which means 'what was to be demonstrated'. It is used in mathematical proofs to indicate that the proof is complete. In the video, the presenter uses a box with an 'x' to symbolize the completion of a proof using the Squeeze Theorem, which is a nod to the traditional use of QED in formal proofs.
Highlights

The Squeeze Theorem, also known as the Pinching Theorem or Sandwich Theorem, is introduced.

The theorem is applicable when a function f(x) is bounded by two other functions h(x) and g(x) on an interval containing c, except possibly at c itself.

If the limits of h(x) and g(x) as x approaches c both equal to l, then the limit of f(x) as x approaches c is also l.

The Squeeze Theorem is used to find limits that are otherwise difficult to compute directly.

An example is given where x times the sine of 1/x as x approaches 0 is evaluated using the Squeeze Theorem.

The sine function is bounded by -1 and 1, which is used to create the necessary inequality for the Squeeze Theorem.

The concept of upper and lower bounds is explained in the context of the sine function.

By multiplying the bounds of the sine function by x, the inequality for the Squeeze Theorem is formed.

The limits of the bounding functions are evaluated as x approaches 0, leading to the conclusion that the original function's limit is also 0.

A second example involves x squared times the cosine of 2022/x to the power of 2021, again approaching 0.

The cosine function is also bounded by -1 and 1, similar to the sine function, and is used to form the inequality.

The process of applying the Squeeze Theorem is demonstrated by evaluating the limits of the bounding functions as x approaches 0.

The conclusion that the limit of the second example is also 0 is reached by the Squeeze Theorem.

The Squeeze Theorem is a common technique in calculus courses, particularly in Calc 1.

The theorem is particularly useful for limits involving trigonometric functions multiplied by x as x approaches 0.

The video provides a step-by-step guide on how to apply the Squeeze Theorem, making it accessible to learners.

The practical application of the Squeeze Theorem is demonstrated through two classic examples, enhancing understanding.

Transcripts

Browse More Related Video

The Squeeze Theorem for Limits, Example 1

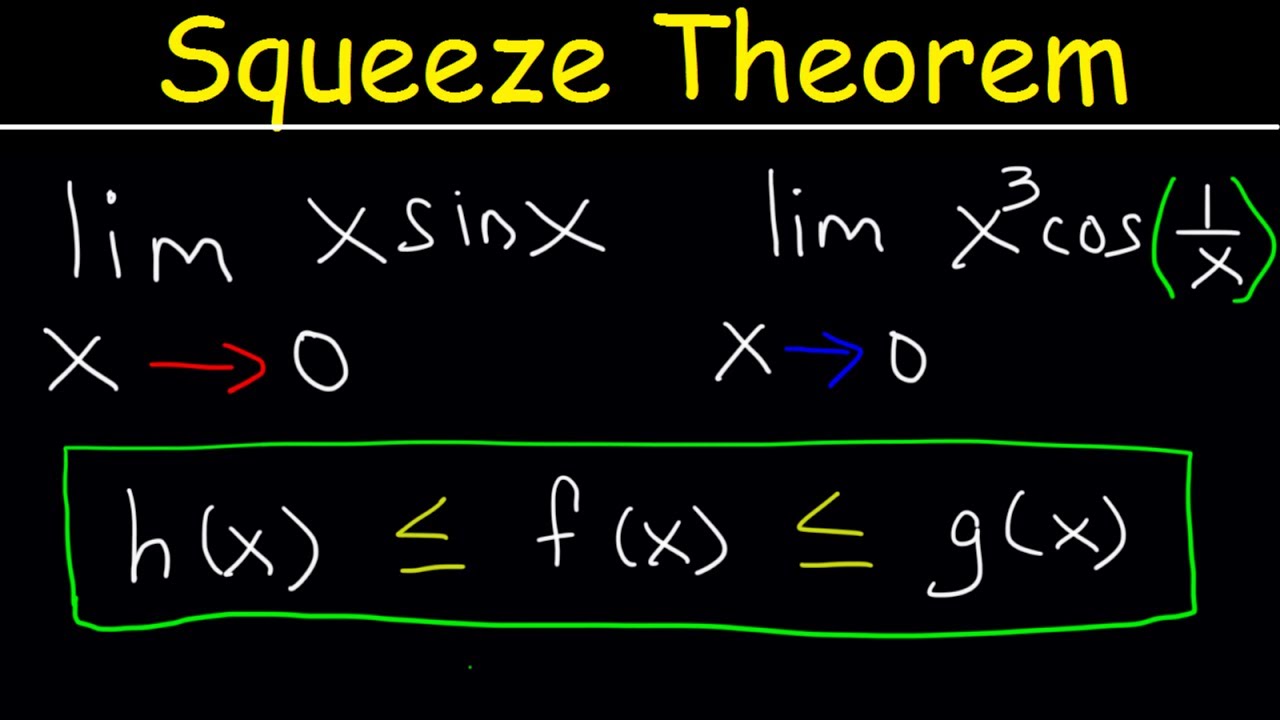
Squeeze Theorem

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

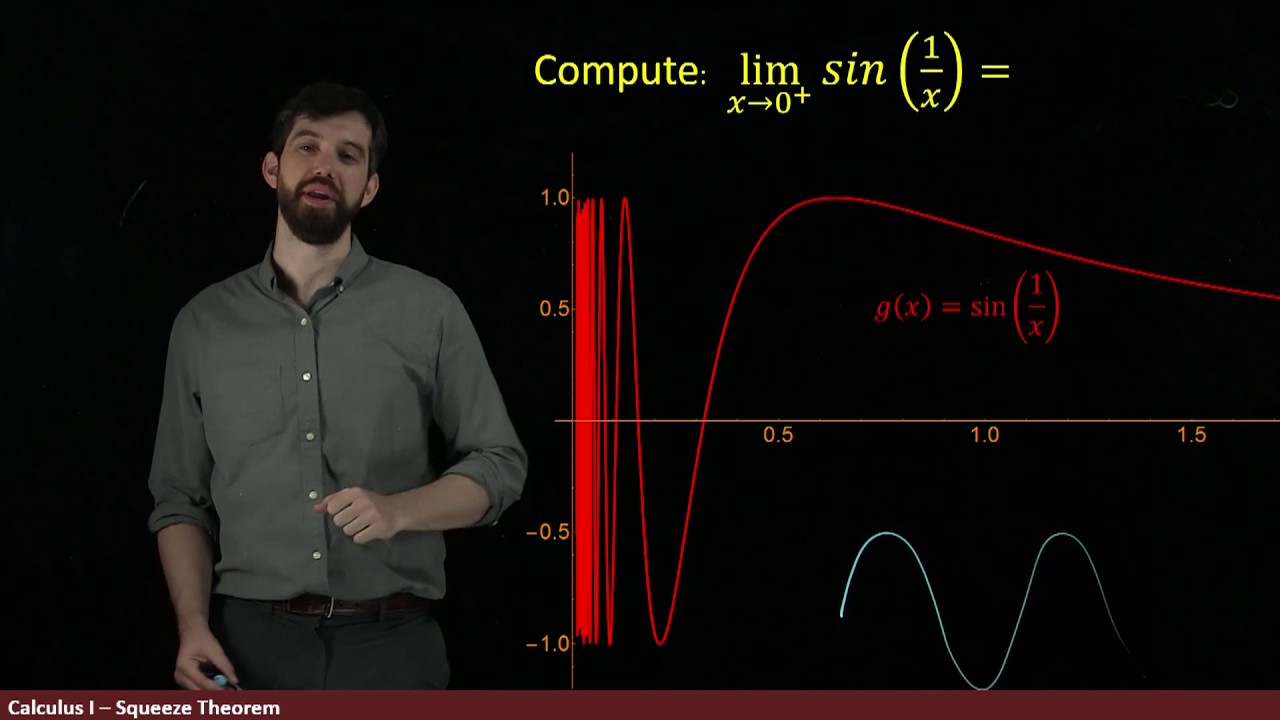
Limits of Oscillating Functions and the Squeeze Theorem

Calculus AB/BC – 1.8 Determining Limits Using the Squeeze Theorem

Squeeze theorem (sandwich theorem) | Limits | Differential Calculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Squeeze TheoremCalculusLimit FindingTrigonometric FunctionsMathematical TechniquesEducational ContentTheoretical MathProblem SolvingX Approaches ZeroSine and Cosine