Squeeze Theorem
TLDRThe video script discusses the concept of the squeeze theorem, a fundamental idea in calculus that helps determine limits of functions. It explains that if a function f(x) is sandwiched between two other functions H(x) and G(x), and the limits of H(x) and G(x) as x approaches a certain value are equal and denoted by L, then the limit of f(x) as x approaches that value must also be L. The script provides several examples to illustrate the application of the theorem, demonstrating how to find limits of functions by applying the squeeze theorem. The examples cover a range of scenarios, including when the functions are polynomials and trigonometric functions, and emphasize the importance of the theorem in understanding the behavior of functions as they approach certain values.
Takeaways
- 📌 The squeeze theorem is a method used to find the limit of a function when it's 'squeezed' between two other functions with known limits.
- 🔢 To apply the squeeze theorem, the given function f(x) must be between two other functions H(x) and G(x), where H(x) ≤ f(x) ≤ G(x).
- 🎯 The key condition for using the squeeze theorem is that the limits of H(x) and G(x) as x approaches a certain value must be equal.
- 🌟 If the limits of the lower and upper bounding functions are the same at a point, then the limit of the middle function at that point must also be equal to this value.
- 📚 Example 1: If f(x) is between 8 - x^3 and 8 + x^3, then the limit as x approaches 0 for f(x) is 8, as demonstrated by direct substitution and the squeeze theorem.
- 📈 Example 2: For the function f(x) between 5x + 2 and x^2 + 8, the limit as x approaches 2 for f(x) is 12, found by evaluating the limits of the bounding functions.
- 🦋 The graph of sin(x) oscillates between -1 and 1, which allows us to apply the squeeze theorem to find that the limit as x approaches 0 for x*sin(x) is 0.
- 🌀 For the function x^3*cos(1/x), since |cos(1/x)| ≤ 1, it follows that the limit as x approaches 0 for x^3*cos(1/x) is also 0.
- 📝 The squeeze theorem can be applied in multiple ways, including direct substitution, dividing parts of the inequality, or evaluating limits at specific points.
- 🎓 Understanding the squeeze theorem is crucial for solving limits, especially when direct substitution or other techniques may not be immediately applicable.
Q & A
What is the main idea behind the squeeze theorem?
-The main idea behind the squeeze theorem is that if a function f(x) is sandwiched between two other functions H(x) and G(x), and the limits of H(x) and G(x) as x approaches a certain value are equal and denoted by L, then the limit of the middle function f(x) as x approaches that value must also be equal to L.
How do you apply the squeeze theorem to find the limit of a function?
-To apply the squeeze theorem, you first identify functions H(x) and G(x) such that H(x) <= f(x) <= G(x) for the values of interest. Then, you find the limits of H(x) and G(x) as x approaches the point in question. If these limits are equal, that common value is the limit of f(x) at that point.
What is the limit as x approaches 0 for the function f(x) = 8 - x^3 and f(x) = 8 + x^3?
-The limit as x approaches 0 for the function f(x) = 8 - x^3 and f(x) = 8 + x^3 is 8. This is because the limit of 8 - 0^3 is 8 and the limit of 8 + 0^3 is also 8, so by the squeeze theorem, the limit of f(x) as x approaches 0 must be 8.
What is the limit as x approaches 2 for the function f(x) that is between 5x + 2 and x^2 + 8?
-The limit as x approaches 2 for the function f(x) that is between 5x + 2 and x^2 + 8 is 12. By evaluating the two bounding functions at x = 2, we get 5*2 + 2 = 12 and 2^2 + 8 = 12, so by the squeeze theorem, the limit of f(x) at x = 2 is 12.
How does the amplitude of the sine function relate to the squeeze theorem?
-The amplitude of the sine function, which is 1, indicates that the function oscillates between -1 and 1, including these values. This property can be used in the squeeze theorem to state that xsinx is between x and x (since x is multiplied by a value between -1 and 1), allowing us to find the limit as x approaches 0, which is 0.
What is the limit as x approaches 0 for the function f(x) = x * sin(x)?
-The limit as x approaches 0 for the function f(x) = x * sin(x) is 0. This is because both x and sin(x) approach 0 as x approaches 0, and their product, according to the squeeze theorem, must also approach 0.
How does the squeeze theorem apply to the function f(x) = x^3 * cos(1/x) as x approaches 0?
-The squeeze theorem applies to the function f(x) = x^3 * cos(1/x) as x approaches 0 by recognizing that cos(1/x) oscillates between -1 and 1. Therefore, the inequality x^3 * -1 <= x^3 * cos(1/x) <= x^3 * 1 holds. As x approaches 0, the limits of x^3 * -1 and x^3 * 1 are both 0, so by the squeeze theorem, the limit of f(x) as x approaches 0 is also 0.
What are the conditions under which the squeeze theorem can be applied?
-The squeeze theorem can be applied when you have a function f(x) that is bounded above and below by two other functions H(x) and G(x), and you can find the limits of these bounding functions as x approaches a certain value. If the limits are equal, you can conclude that the limit of f(x) at that point is also equal to this common limit.
How does direct substitution play a role in applying the squeeze theorem?
-Direct substitution is often used to evaluate the limits of the bounding functions H(x) and G(x) as x approaches the point of interest. By substituting the value into these functions, we can determine the bounds for the limit of the middle function f(x) using the squeeze theorem.
What is the significance of the squeeze theorem in calculus?
-The squeeze theorem is significant in calculus as it provides a powerful tool for finding limits of functions, especially in cases where direct substitution or other standard limit-finding techniques may not be applicable or straightforward. It offers a way to approach complex limits by simplifying them through bounding functions.
Can the squeeze theorem be used for functions that do not have defined limits?
-The squeeze theorem can be used for functions that do not have defined limits in certain circumstances. If the bounding functions H(x) and G(x) have the same one-sided limits and the middle function f(x) is sandwiched between them, the squeeze theorem can still be applied to find the value of the limit, which may be infinite or undefined (±∞).
Outlines
📚 Introduction to the Squeeze Theorem
This paragraph introduces the concept of the Squeeze Theorem, a fundamental idea in calculus used to determine limits of functions. It explains that if a function f(x) is bounded between two other functions H(x) and G(x), and the limits of H(x) and G(x) as x approaches a certain value are equal and denoted by L, then the limit of f(x) as x approaches that value must also be L. The explanation is supported by an example where f(x) is bounded by 8 - x^3 and 8 + x^3, and the limit as x approaches 0 is determined to be 8 by applying the theorem.
📈 Application of the Squeeze Theorem with sin(x)
In this paragraph, the Squeeze Theorem is applied to the function f(x) = x * sin(x) as x approaches 0. The graph of sin(x) is discussed, noting that it oscillates between -1 and 1. By multiplying sin(x) by x, the function is bounded between x and positive X, and the limits at x approaches 0 are evaluated for both bounds, resulting in a value of 0. This demonstrates that the limit of x * sin(x) as x approaches 0 is also 0, confirming the validity of the Squeeze Theorem for this scenario.
🔢 Solving Limits with X Cubed and Cosine Function
The final paragraph discusses another application of the Squeeze Theorem, this time with the function f(x) = x^3 * cos(1/x). It explains that since the cosine function oscillates between -1 and 1, multiplying it by x^3 results in a function bounded between negative x^3 and positive x^3. By evaluating the limits as x approaches 0 for each part of the inequality, it is determined that the limit must be 0. This reinforces the understanding and application of the Squeeze Theorem for different types of functions.
Mindmap
Keywords
💡squeeze theorem
💡limit
💡function
💡inequality
💡approaches
💡direct substitution
💡amplitude
💡oscillate
💡range
💡domain
Highlights
The main idea of the squeeze theorem is introduced, which states that if a function f(x) is between two other functions H(x) and G(x), and the limits of H(x) and G(x) as x approaches a certain value are equal, then the limit of f(x) as x approaches that value must also be equal to that value.
A practical example is given where f(x) is between 8 - x^3 and 8 + x^3, and the limit of f(x) as x approaches 0 is determined to be 8 by applying the squeeze theorem.
The process of applying the squeeze theorem is demonstrated by applying limits to each expression in the inequality and then using direct substitution to find the common limit.
Another example is solved where f(x) is between 5x + 2 and x^2 + 8, and the limit as x approaches 2 of f(x) is found to be 12 using the squeeze theorem.
The graph of sin(x) is discussed, noting that its amplitude is one, and thus sin(x) lies between -1 and 1, including those values.
By multiplying the inequality x sin(x) by x, the squeeze theorem is applied to find that the limit as x approaches 0 for x sin(x) must be 0.
The squeeze theorem is applied to a more complex function involving x^3 and the cosine function, where the limit as x approaches 0 is also determined to be 0.
The transcript provides a clear and detailed explanation of the squeeze theorem, its application, and its significance in understanding limits.
The use of direct substitution in conjunction with the squeeze theorem is demonstrated to solve for limits in a straightforward manner.
The transcript emphasizes the importance of understanding the relationship between the limits of the upper and lower functions in the squeeze theorem and how they dictate the limit of the middle function.
The concept of the squeeze theorem is reinforced through multiple examples, each with a step-by-step breakdown of the process.
The transcript highlights the versatility of the squeeze theorem in solving for limits of various types of functions, including polynomial and trigonometric functions.
The practical applications of the squeeze theorem in determining limits are clearly illustrated, providing a solid foundation for further study and understanding of calculus concepts.
The transcript effectively uses visual aids, such as graphs and inequalities, to enhance the reader's comprehension of the squeeze theorem.
The transcript concludes with a summary that reinforces the key points and leaves the reader with a clear understanding of how to apply the squeeze theorem.
Transcripts
Browse More Related Video

The Squeeze Theorem for Limits, Example 1
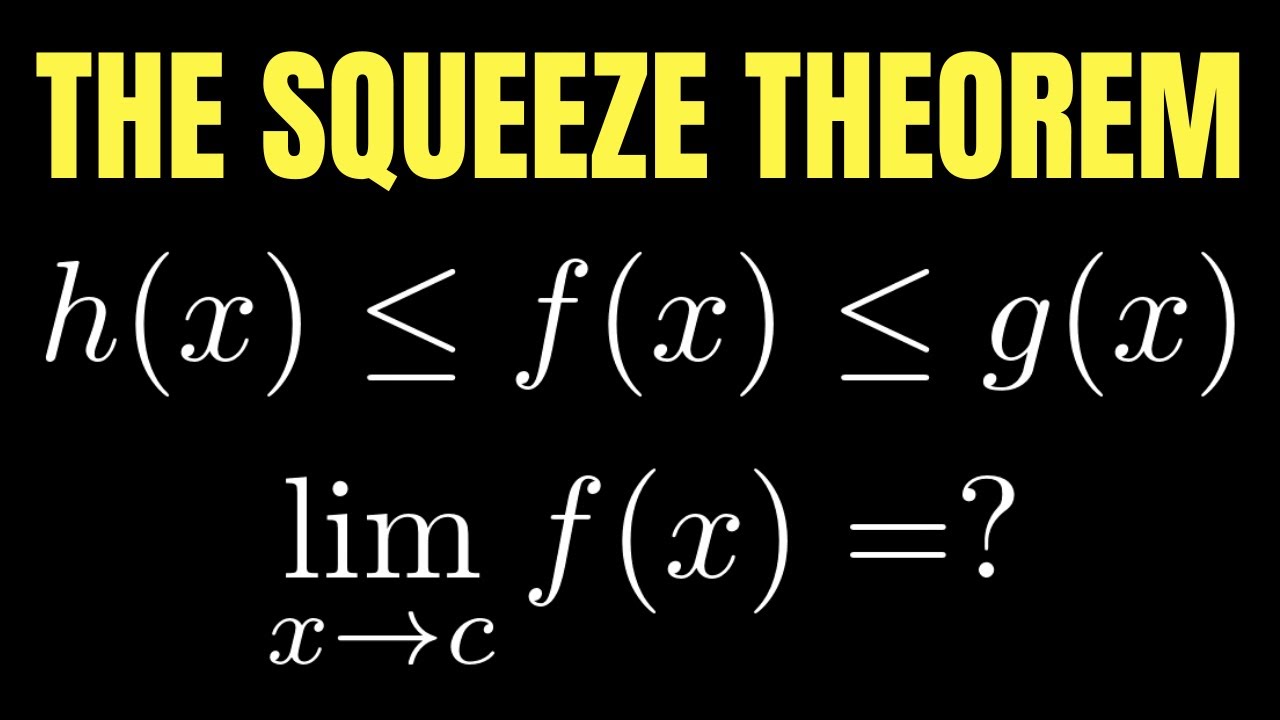
Calculus: The Squeeze Theorem Full Tutorial

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus
2019 AP Calculus AB FRQ #6

A Tale of Three Functions | Intro to Limits Part II
A Tale of Three Functions | Intro to Limits Part I
5.0 / 5 (0 votes)
Thanks for rating: