What Is Circular Motion? | Physics in Motion
TLDRIn this episode of 'Physics In Motion,' Adrian Monte explores the physics behind circular motion, explaining that even at constant speed, objects in a circle are accelerating due to changing direction. He delves into centripetal force, which keeps objects moving in a circle, and illustrates this with examples like swinging a bucket of water and the forces at play during a roller coaster ride. The video clarifies misconceptions about centrifugal force, emphasizing it's not a real force but a result of inertia. The script also covers concepts such as tangential velocity, period of revolution, and centripetal acceleration, providing a comprehensive look at the physics of circular motion.
Takeaways
- 🔄 Objects moving in a circle at a constant speed are still accelerating due to the continuous change in direction.
- 📉 Velocity is a vector quantity with both magnitude and direction, and a change in either results in acceleration.
- 🪣 Centripetal force, represented as ( F_c ), is the net force that keeps an object moving in a circular path.
- 🔗 Different forces such as friction, tension, normal force, or gravity can act as centripetal forces depending on the situation.
- 🚿 When swinging a bucket of water, the combination of gravity and tension force creates the centripetal force that keeps the bucket moving in a circle.
- 🌐 At the bottom of a circular path, the normal force from the bucket's bottom, along with tension, keeps the water moving in a circle.
- 🪢 The tension of a rope is what keeps a satellite in orbit around Earth, with gravity acting as the centripetal force.
- 🛤️ Frictional force helps keep a cart moving in a circular track by allowing the tires to grip the track.
- 💥 The sensation of being thrown to one side in a car during a sharp turn is due to inertia, not centrifugal force.
- 🎢 Tangential velocity ( V_T ) is the velocity of an object moving in a circle along the tangent to the circle's path.
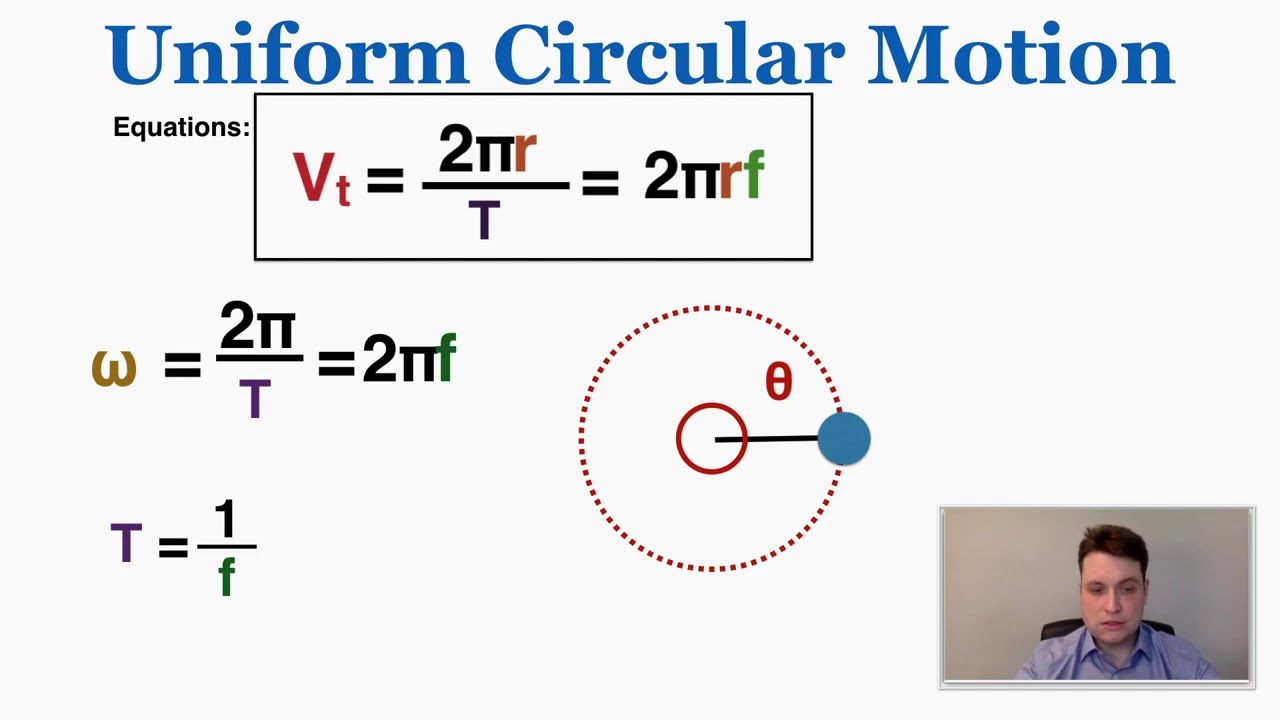
- ⏱ The period of revolution (T) is the time it takes for an object to complete one full circle in uniform circular motion.
- 📐 Centripetal acceleration is perpendicular to the tangential velocity and is calculated as ( V_T^2 / r ), where ( V_T ) is the tangential velocity and ( r ) is the radius of the circle.
Q & A
What is the primary reason for the object's acceleration when it is moving in a circular path at a constant speed?
-An object is accelerating when moving in a circular path at a constant speed because its direction is constantly changing. Even though the speed (magnitude of velocity) is constant, the direction of the velocity vector changes, resulting in acceleration.
Can you explain the concept of centripetal force?
-Centripetal force is the net force acting on an object that keeps it moving in a circular path. It is often referred to as 'center seeking' and is represented as F_sub_C. It can be caused by various forces such as friction, tension, the normal force, or gravity, depending on the situation.
Why doesn't water spill out of a bucket when it is swung in a circle?
-The water doesn't spill out of the bucket because of the centripetal force acting on it. This force, which can be provided by tension in the rope holding the bucket, keeps the water moving in a circular path and prevents it from falling out due to inertia.
What are the forces acting on the bucket when it is at the top of the swing?
-At the top of the swing, the forces acting on the bucket are gravity (F_sub_G), which acts downward, and tension (F_sub_T), which acts towards the center of the circle. These forces combine to create the centripetal force that keeps the bucket moving in a circle.
What force keeps the water in the bucket when it is at the bottom of the loop?
-At the bottom of the loop, the normal force from the bucket's bottom on the water's inertia keeps the water in the bucket. This normal force, combined with the tension force that keeps the bucket moving in a circle, ensures the water stays inside.
How does gravity act as a centripetal force for a satellite orbiting Earth?
-Gravity pulls the satellite toward Earth, providing the necessary centripetal force to keep the satellite in orbit. This force acts as a tether, preventing the satellite from flying off into space and keeping it moving around a central point.
What is the difference between the forces acting on a cart in a circular track compared to a bucket of water swinging in vertical circles?
-The main difference is the orientation of the circular motion. While the bucket swings in vertical circles, the cart moves in a horizontal circular track. However, the principle of centripetal force remains the same, with frictional force helping the tires grip the track and maintain the cart's circular path.
What is the misconception about the force felt when making a sharp turn in a car?
-The misconception is that the force felt is due to centrifugal force. In reality, it is caused by Newton's First Law, which states that an object in motion tends to stay in motion. When the car turns, the body wants to continue in a straight line due to inertia, and the force felt is the car's seat pushing against you as it turns.
What is tangential velocity and why is it significant in the context of circular motion?
-Tangential velocity (V_sub_T) is the velocity of an object moving along the tangent to the circle at any given point in its circular path. It is significant because if the centripetal force were to suddenly disappear, the object would move in a straight line at this tangential velocity.
What is the relationship between the period of revolution and the tangential velocity of an object in uniform circular motion?
-The tangential velocity of an object in uniform circular motion is equal to the distance around the circumference (which is 2π times the radius) divided by the period of revolution (T). This relationship shows how the object's speed and the time it takes to complete one full circle are related.
How is centripetal acceleration calculated and what is its direction?
-Centripetal acceleration is calculated as the tangential velocity squared, divided by the radius of the circle. It is always perpendicular to the tangential velocity and acts in the same direction as the centripetal force, which is toward the center of the circle.
Can you provide an example of how to calculate the normal force exerted on a person at the bottom of a roller coaster loop?
-Using Newton's Second Law, the normal force (N) can be calculated by rearranging the equation N - mg = m(V_t^2 / r), where m is mass, g is acceleration due to gravity, V_t is tangential velocity, and r is the radius of the loop. By substituting the given values and solving for N, you can find the normal force experienced.
Outlines
🎢 Physics of Circular Motion and Centripetal Force
In this paragraph, Adrian Monte explores the physics behind circular motion, particularly at an amusement park. He explains that even when moving at a constant speed in a circle, an object is still accelerating due to the continuous change in direction. This acceleration is due to the centripetal force, which is the net force acting on an object to keep it in a circular path. Monte uses the example of swinging a bucket of water to illustrate centripetal force, explaining how gravity and tension work together to keep the bucket moving in a circle and the water inside it. He further discusses the role of different forces such as friction, tension, normal force, and gravity in providing centripetal force in various scenarios, including satellites orbiting Earth. The paragraph concludes with a look at the forces at play when a cart moves around a circular track, emphasizing the role of frictional force in maintaining the cart's circular path.
🌀 Understanding Tangential Velocity, Period, and Centripetal Acceleration
This paragraph delves into the concepts of tangential velocity, period of revolution, and centripetal acceleration in the context of uniform circular motion. Monte explains that tangential velocity is the velocity of an object moving along the circumference of a circle and is directed tangentially to the circle. He describes the period of revolution as the time taken for one complete circular motion. Using the formula for circumference and the definition of tangential velocity, Monte demonstrates how to calculate the centripetal acceleration, which is perpendicular to the tangential velocity and directed toward the center of the circle. He also applies Newton's Second Law to explain how the sum of centripetal forces equals the mass times the centripetal acceleration. The paragraph includes a practical example involving a roller coaster ride, where Monte calculates the normal force experienced by a rider at the bottom of a loop using the concepts discussed. The segment ends with a reminder of the importance of these principles in understanding the physics of motion in various real-world scenarios.
Mindmap
Keywords
💡Acceleration
💡Velocity
💡Centripetal Force
💡Inertia
💡Tangential Velocity
💡Period of Revolution
💡Circumference
💡Centripetal Acceleration
💡Normal Force
💡Newton's Laws
Highlights
Visiting Wild Adventures to learn about physics through circular motion.
Explaining that constant speed in a circular path still involves acceleration due to changing direction.
Clarification of velocity as a vector quantity with magnitude and direction.
Introduction to centripetal force with the example of swinging a bucket of water.
Centripetal force defined as the net force keeping objects moving in a circle.
Different types of centripetal forces such as friction, tension, normal force, and gravity.
Analysis of forces acting on a bucket of water at the top of a swing.
Explanation of how gravity and tension create centripetal force.
Discussion on the forces at work when the bucket is at the bottom of a loop.
The role of the normal force in keeping water in the bucket during circular motion.
Satellite orbiting Earth as an example of centripetal force being Earth's gravity.
The importance of velocity for a satellite to maintain orbit.
Frictional force as the key to keeping a cart in a circular path on a track.
Centrifugal force debunked as not a real force, explained by Newton's First Law.
Inertia's role in the sensation of being slammed against a car door during a sharp turn.
Tangential velocity and its relationship with the object's motion in a circle.
Period of revolution and its calculation for objects in circular motion.
Calculating tangential velocity using the circumference and period.
Centripetal acceleration formula and its perpendicular direction to tangential velocity.
Newton's Second Law applied to centripetal forces and acceleration.
Example calculation of normal force during a roller coaster ride.
Comparing the normal force felt on a roller coaster to standing on the ground.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: