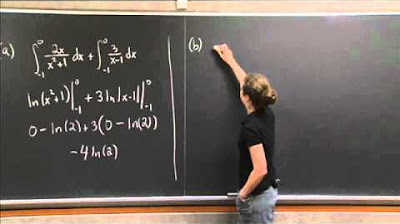7.5 WebAssign Discussion
TLDRThis video offers an in-depth discussion on strategies for integration, covering techniques such as integration by parts, trigonometric substitution, and partial fraction decomposition. The instructor provides step-by-step guidance on when and how to apply these methods to various integrals, using specific examples to illustrate the process. The session is designed to prepare students for exams by practicing these fundamental calculus skills.
Takeaways
- 📚 The video discusses various integration strategies covered in section 7.5, including integration by parts, trigonometric substitution, and partial fraction decomposition.
- 🔍 The script emphasizes the importance of choosing the right technique for different integral expressions, such as recognizing when to use trigonometric substitution based on the form of the polynomial inside a square root.
- 📉 The video clarifies that certain expressions, like '1 + x', do not lend themselves to certain substitutions due to the absence of specific derivatives in the integral.
- 🌟 A key point is made about setting 'u' equal to functions like '1 - sin^2(theta)' which simplifies to 'cos^2(theta)', illustrating the use of trigonometric identities in substitutions.
- 🔑 The script introduces a method for substitution when dealing with expressions like 'x + 5', where 'u' is set to 'x + 5' and 'du' is 'dx', simplifying the integral.
- 📝 The video provides examples of integrals that require different techniques, such as using integration by parts for '(1 + x^2)^3' and inverse trigonometric functions for '1/(1 + x^2)'.
- 📉 For integrals involving logarithmic functions, the video suggests using substitution with 'u = ln(x)', which simplifies the process by canceling out terms.
- 🔄 The script explains the use of integration by parts for integrals with logarithmic functions, where 'u' is set to 'ln(x)' and 'dv' is determined accordingly.
- 📈 The video highlights the use of trigonometric identities for integrals with powers of sine and cosine, such as using the identity for 'sin^3(x)' when integrating odd powers.
- 📌 The script touches on the concept that not all elementary functions have elementary anti-derivatives, pointing out that 'ln(x)' is transcendental and not elementary.
- 🎓 The final takeaway is that mastering these integration techniques is excellent preparation for a final exam, emphasizing the practical application of the concepts discussed.
Q & A
What is the main topic of the video?
-The main topic of the video is discussing various strategies for integration, including techniques such as integration by parts, trigonometric substitution, and partial fraction decomposition.
Why is the expression with a square root and a degree 2 polynomial inside a classic trigonometric substitution scenario?
-It is a classic trigonometric substitution scenario because the square root often simplifies when the polynomial inside can be expressed in terms of trigonometric identities, making the integral more manageable.
What substitution is suggested for the integral involving 1 - sin squared theta?
-The substitution suggested is u = cos(theta), because 1 - sin squared theta is equivalent to cos squared theta, simplifying the integral.
Why is the substitution u = x + 5 used in the integral with x + 5 under a square root?
-The substitution u = x + 5 is used because it simplifies the expression under the square root to u, making the integral easier to solve by separating the dx and du.
What is the first integral technique used in the video for the expression with 1 + x squared in the denominator?
-The first integral technique used is integration by parts, because the derivative of (1 + x) squared is related to the function in the integral.
Why can't the integral with 1 over 1 plus x squared be solved using u-substitution?
-It can't be solved using u-substitution because the expression does not simplify in a way that allows for a straightforward substitution to be made.
What is the reason for using inverse trigonometric functions for the integral with 1 over 1 plus x squared?
-Inverse trigonometric functions are used because the integral can be expressed in terms of an inverse trigonometric identity, which simplifies the process of integration.
How does the video suggest solving the integral with a logarithmic function in the denominator?
-The video suggests using u-substitution with u = ln(x), as the derivative of ln(x) is 1/x, which simplifies the integral.
Why is integration by parts suggested for the integral with ln(x) and a factor of 2x?
-Integration by parts is suggested because the product of ln(x) and 2x does not have a straightforward antiderivative, and integration by parts allows for breaking down the integral into simpler parts.
What is the reason for using partial fraction decomposition for the integral with 1 - x squared in the denominator?
-Partial fraction decomposition is used because the denominator can be factored into linear terms, allowing for the integral to be broken down into simpler fractions that are easier to integrate.
What is the significance of the statement 'Every elementary function has an elementary derivative' in the context of the video?
-The statement highlights the fact that while every elementary function can be differentiated to get another elementary function, not every elementary function has an elementary antiderivative, as some require non-elementary functions like the natural logarithm.
Outlines
📚 Integration Techniques Overview
This paragraph introduces a discussion on integration strategies, focusing on section 7.5. It covers various techniques such as integration by parts, trigonometric substitution, and partial fraction decomposition. The speaker emphasizes the importance of choosing the right technique for different integrals, such as recognizing when to use trigonometric substitution based on the form of the polynomial under the square root. The paragraph also discusses specific substitution scenarios, like setting u equal to x + 5 to simplify the integral, and highlights the need to understand when to apply each technique for effective problem-solving in calculus.
🔍 Advanced Integration Strategies and Examples
The second paragraph delves deeper into the application of integration techniques with a variety of examples. It discusses the use of substitution (u-sub) for integrals involving logarithmic functions and even powers of trigonometric functions, as well as integration by parts for cases with odd powers of sine and cosine. The speaker also addresses the use of inverse trigonometric functions for certain integrals and the process of partial fraction decomposition for rational functions. The paragraph provides a comprehensive overview of how to approach complex integrals by applying the appropriate method, including handling definite integrals and the use of trigonometric identities.
📘 Reflections on Elementary Functions and Integration Practice
In the final paragraph, the speaker reflects on the nature of elementary functions and their anti-derivatives, noting that while all elementary functions have elementary derivatives, not all have elementary anti-derivatives, such as 1/x which anti-derives to the transcendental function ln(x). The paragraph concludes with a summary of the importance of practicing various integration techniques, emphasizing that mastering these methods is crucial for success in exams. The speaker encourages students to use the exercises provided as a means to prepare thoroughly for their final exams.
Mindmap
Keywords
💡Integration Techniques
💡Integration by Parts
💡Trigonometric Substitution
💡Partial Fraction Decomposition
💡U-Substitution
💡Inverse Trigonometric Functions
💡Elementary Functions
💡Transcendental Functions
💡Double Angle Formulas
💡Definite Integral
💡Irreducible Degree
Highlights
Introduction to Section 7.5 focusing on integration strategies.
Discussion of various integration techniques including integration by parts, trigonometric substitution, and partial fraction decomposition.
Identification of a classic trigonometric substitution scenario with a square root and a degree 2 polynomial.
Explanation of why U-substitution won't work due to the derivative of 1+x not being present in the integral.
Introduction of a U-substitution with 1-sin^2(theta) equaling cosine^2, for an odd power of sine and cosine.
Strategy for U-substitution with x + 5 as the inside function and the simplification it brings.
Evaluation of integrals using U-substitution, inverse trigonometric functions, and partial fraction decomposition.
Explanation of how to handle integrals with the LM function using U-substitution with ln(x).
Use of integration by parts for integrals involving the natural logarithm function.
Discussion on trigonometric integrals with even powers of sine and the application of double angle formulas.
Strategy for dealing with odd powers of sine and cosine using U-substitution with u = cos(x).
Evaluation of an integral with 6 - sin(x) using U-substitution and the simplification it provides.
Approach to partial fraction decomposition for integrals with quadratic factors in the denominator.
Use of U-substitution for an integral with an exponential function inside another function.
Discussion on powers of tangent and secant and the use of U-substitution with u = tan(x).
Trigonometric substitution for an integral with 81x^2 + 1 using x = 1/sqrt(81) * tan(θ).
Reflection on the statement that every elementary function has an elementary anti-derivative, with a clarification on transcendental functions.
Conclusion emphasizing the value of the exercise set for final exam preparation.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: