Pre Calculus - Solving System of Nonlinear Equations | Systems of Equations

MATH TEACHER GON
2 Oct 202119:33
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script introduces viewers to solving systems of non-linear equations, a topic that extends beyond the linear equations taught in junior high. The script provides two examples of such systems and demonstrates the use of the substitution method to find solutions. It guides through the process of isolating variables, substituting values, and simplifying equations to solve for x and y. The video also emphasizes the importance of verifying solutions by substituting them back into the original equations.

Takeaways
  • 📚 The video is about solving systems of non-linear equations, which are sets of two or more equations with at least one non-linear equation.
  • 🔍 Non-linear equations are distinguished from linear ones by having variables raised to a power higher than one, such as quadratic equations.
  • 📝 The script provides two examples of non-linear systems: one with x^2 + y^2 = 25 and 3x + 4y = 0, and another with x^2 + y = 2 and y = -x + 2.
  • 🛠 The substitution method is used to solve the second example, where a linear equation is manipulated to express one variable in terms of the other.
  • 🔢 After substituting the expression for y into the non-linear equation, the script demonstrates the process of expanding and simplifying to form a quadratic equation.
  • 🔍 The quadratic equation is then factored and solved for x, yielding x = 1 as one of the solutions.
  • 📐 Subsequently, the value of x is substituted back into the linear equation to solve for y, resulting in y = 1.
  • 🔄 The script emphasizes the importance of checking the solution by substituting the values of x and y back into the original equations to ensure they satisfy both.
  • 📉 For the first example, the script isolates y in the linear equation to express it in terms of x, and then substitutes this into the non-linear equation to solve for x.
  • 🔢 The solution process involves simplifying the equation to form a quadratic in terms of x, which is then solved to find the possible values of x.
  • 📌 After finding the values of x, the script shows how to find the corresponding y values using the linear equation, resulting in multiple solutions for the system.
  • 🗣️ The video concludes with an invitation for viewers to ask questions in the comments and a reminder to like, subscribe, and hit the bell for updates.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving systems of non-linear equations.

  • What is a system of non-linear equations?

    -A system of non-linear equations consists of two or more equations with at least one equation that is not linear, meaning the highest exponent of the variable is not one.

  • What are the common methods to solve systems of linear equations?

    -The common methods to solve systems of linear equations are the elimination method, the substitution method, and the graphical method.

  • How does the degree of an equation relate to it being linear or non-linear?

    -An equation is linear if the degree of the given equation is one, meaning the highest exponent of the variable is one. If the degree is higher than one, it is considered non-linear.

  • What substitution method does the teacher use in the video to solve the first example?

    -The teacher uses the substitution method by first solving the linear equation for y and then substituting this expression for y into the non-linear equation.

  • In the first example, what is the process of solving for y after finding the value of x?

    -After finding the value of x, the teacher substitutes this value into the linear equation (y = -x + 2) to solve for y.

  • What is the purpose of checking the solution in the context of the video?

    -The purpose of checking the solution is to verify whether the found values of x and y satisfy both equations in the system of non-linear equations.

  • What is the strategy used in the second example to solve for y in terms of x?

    -The strategy used in the second example is to isolate y in the linear equation (3x + 4y = 0) and express y in terms of x as y = -3x/4.

  • How does the teacher simplify the equation after substituting y in terms of x in the second example?

    -The teacher multiplies the entire equation by 16 to eliminate the fraction and then simplifies it to a quadratic equation in terms of x.

  • What are the final solutions for the second example of the system of non-linear equations?

    -The final solutions for the second example are (x, y) = (4, -3) and (x, y) = (-4, 3).

  • How can viewers get updates on the latest uploads from the channel?

    -Viewers can hit the like and subscribe button and also hit the bell button to get updates on the latest uploads from the channel.

Outlines
00:00
📚 Introduction to Solving Non-linear Systems

The video script begins with an introduction to the topic of solving systems of non-linear equations. The instructor explains the difference between linear and non-linear equations, emphasizing that non-linear systems involve at least one equation where the highest exponent of the variable is greater than one. Two examples of non-linear systems are provided, illustrating the concept with a quadratic equation and a linear one combined, and another with a non-linear equation and a linear equation for y in terms of x.

05:01
🔍 Substitution Method for Non-linear Systems

The second paragraph delves into the substitution method for solving non-linear systems. The instructor demonstrates how to isolate a variable in a linear equation and then substitute this expression into a non-linear equation to solve for the other variable. Using the example of the system where y is expressed in terms of x, the instructor shows the process of substitution and simplification, leading to a quadratic equation in terms of x, which is then factored and solved for x.

10:04
📉 Solving for x and Verifying the Solution

In the third paragraph, the instructor continues the solution process by finding the value of y using the previously determined value of x. The solution for y is found by substituting x back into one of the original equations. The instructor then explains the importance of verifying the solution by substituting the values of x and y back into both original equations to ensure they satisfy the system. The verification confirms that the solution is correct.

15:04
🔧 Solving the Second Non-linear System Example

The final paragraph presents the solution to the second example of a non-linear system. The instructor chooses to isolate y in the linear equation and then substitute this expression into the quadratic equation to solve for x. After finding the values of x, the instructor proceeds to find the corresponding values of y by substituting x back into the linear equation. Two sets of solutions for x and y are obtained and presented, and the instructor encourages viewers to check the solutions in the original equations.

Mindmap
Keywords
💡Systems of Non-Linear Equations
A system of non-linear equations refers to a collection of two or more equations where at least one equation is not linear, meaning it has a variable raised to a power higher than one. In the video's context, these systems are the main focus, and the teacher discusses methods for solving them. For example, the script mentions equations like 'x squared plus y squared is equal to 25', which is non-linear due to the squared terms.
💡Degree of an Equation
The degree of an equation is the highest power of the variable in the equation. It is used to distinguish between linear and non-linear equations. In the script, the teacher explains that linear equations have a degree of one, while non-linear equations, which are the focus of the video, have a degree greater than one, as seen in 'x squared'.
💡Substitution Method
The substitution method is a technique used to solve systems of equations by expressing one variable in terms of another and then substituting this expression into the other equation(s). The script illustrates this method by solving for 'y' in terms of 'x' and then substituting this into the non-linear equation to find the values of 'x' and 'y'.
💡Linear Equation
A linear equation is an algebraic equation in which the highest power of the variable is one. The video contrasts linear equations with non-linear ones, explaining that linear equations can be solved using methods like elimination, substitution, or graphical methods, which are different from those used for non-linear equations.
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two, which typically takes the form ax^2 + bx + c = 0. In the script, the teacher encounters a quadratic equation when substituting 'y' in terms of 'x' into the first equation, resulting in an equation that can be solved by factoring or using the quadratic formula.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of its factors. In the video, after expanding and simplifying the equation, the teacher factors out a common term to solve for 'x', demonstrating how factoring can be used to simplify and solve quadratic equations.
💡Graphical Method
The graphical method involves plotting the equations on a graph and finding the point(s) of intersection, which represent the solution(s) to the system of equations. Although not explicitly used in the script's examples, the teacher mentions it as one of the methods for solving systems of linear equations, which can also be applied to non-linear systems.
💡Elimination Method
The elimination method is a technique for solving systems of equations by adding or subtracting the equations to eliminate one variable, making it possible to solve for the other. The script briefly mentions this method as one used for linear systems, but it is not demonstrated in the non-linear examples given.
💡Checking Solutions
Checking solutions involves substituting the found values of variables back into the original equations to verify that they satisfy all equations in the system. The script emphasizes the importance of this step to ensure the correctness of the solutions obtained for the non-linear systems.
💡Variable
In algebra, a variable represents an unknown value that can change. In the context of the video, variables 'x' and 'y' are used in the equations to be solved. The teacher discusses isolating variables and solving for them, as seen when solving for 'y' in terms of 'x' or vice versa.
💡Exponent
An exponent indicates the number of times a base number is multiplied by itself. In non-linear equations, variables can have exponents greater than one, which distinguishes them from linear equations. The script uses terms like 'x squared' to illustrate the presence of exponents in non-linear equations.
Highlights

Introduction to the topic of solving systems of non-linear equations.

Definition of a system of non-linear equations, consisting of two or more equations with at least one non-linear equation.

Explanation of linear equations and their degree, contrasting with non-linear equations.

Overview of methods to solve systems of linear equations: elimination, substitution, and graphical methods.

Two example systems of non-linear equations are presented for demonstration.

Description of the first example with a quadratic equation and a linear equation.

Description of the second example with a non-linear equation and a linear equation.

Introduction of the substitution method for solving non-linear systems, starting with the linear equation.

Step-by-step substitution process using the linear equation to solve for a variable.

Expansion of the substituted expression using the FOIL method.

Simplification of the equation to form a quadratic equation.

Factoring and solving the quadratic equation to find the value of x.

Using the found value of x to solve for y using the second equation.

Verification of the solution by substituting x and y back into the original equations.

Introduction of the second example with a different pair of equations.

Isolating y in the linear equation to temporarily solve for y in terms of x.

Substituting the expression for y into the quadratic equation to solve for x.

Simplifying and solving the resulting quadratic equation for x.

Finding the corresponding values of y for each x using the linear equation.

Consolidating the solutions for the system of equations and verifying them.

Conclusion of the tutorial with an invitation for questions and further engagement.

Transcripts

Browse More Related Video

Logarithmic Equations

7.1.1 Solving a System of Equations Using Substitution

Solving Systems of Equations By Elimination & Substitution With 2 Variables

Cramer's Rule - 2x2 & 3x3 Matrices - Solving Systems of Linear Equations - 2 & 3 Variables

PreCalculus - Matrices & Matrix Applications (26 of 33) Solving Sys of Linear Eqn with Inverse

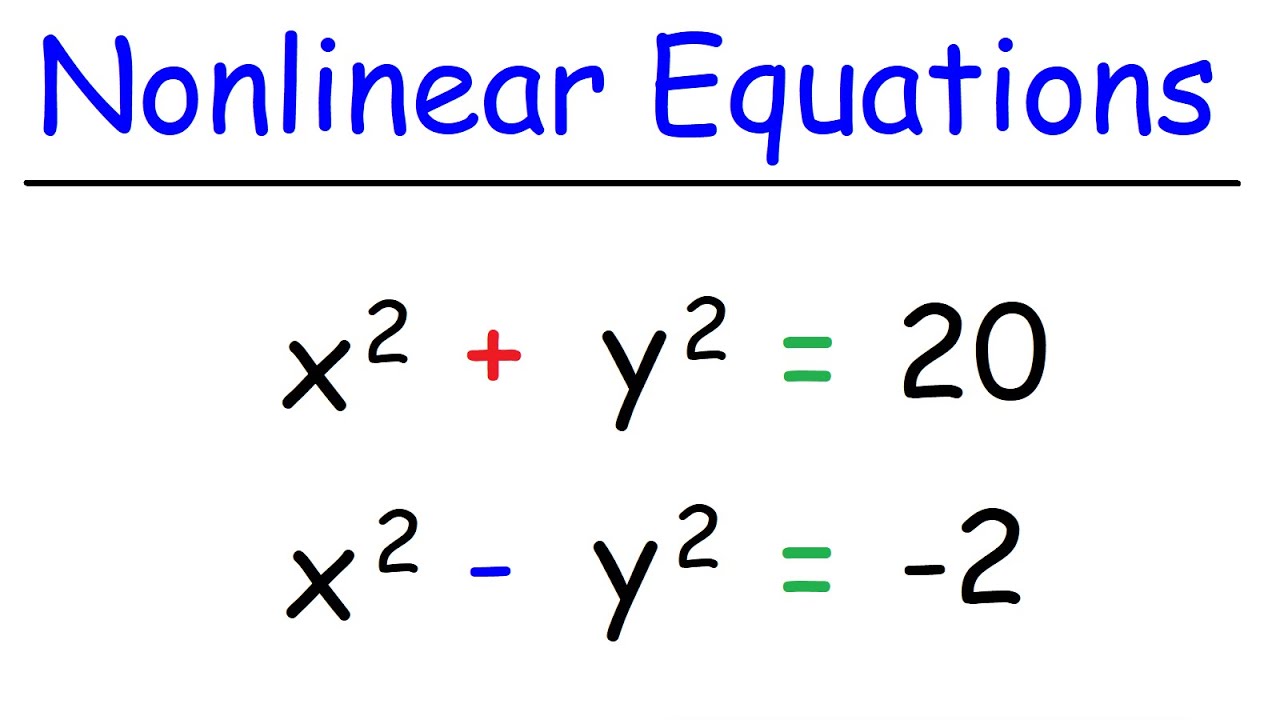
How To Solve Systems of Nonlinear Equations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Non-linear SystemsEquation SolvingMathematics TutorialEducational ContentSubstitution MethodAlgebraic TechniquesQuadratic EquationsLinear EquationsGraphical MethodMath Teaching