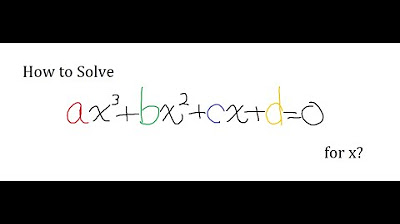so you want to see the cubic formula

blackpenredpen

18 Apr 202340:16

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script guides viewers through solving cubic equations by deriving the cubic formula. It begins with a review of solving quadratic equations, introducing the PQ formula, and then transitions into tackling cubic equations. The process involves a series of algebraic manipulations, including completing the square and the use of the Cardano's substitution. The script also touches on complex analysis and introduces the concept of cube roots of unity to find all three solutions to the cubic equation, promising a follow-up on applying the cubic formula to trigonometric problems.

Takeaways

📚 The video begins with a review of solving quadratic equations, introducing the standard form \( ax^2 + bx + c = 0 \) and the process of completing the square.
🔍 The presenter explains the concept of 'translating' the graph of a quadratic equation to eliminate the first power term by substituting \( x = y - \frac{b}{2a} \).
📈 The method of completing the square is demonstrated through a visual approach, showing the transformation of the quadratic equation into a form that allows for easy root extraction.
📝 The script transitions into solving cubic equations, emphasizing the standard form and the goal of eliminating the second power term through a similar translation technique.
🧠 The 'Tschirnhaus substitution' is introduced as a method to transform a cubic equation into a quadratic form in terms of \( z \), where \( y = z - \frac{b}{3a} \).
🔑 The video demonstrates the algebraic manipulation required to achieve the Tschirnhaus substitution, resulting in a quadratic equation in terms of \( z^3 \).
📉 The presenter uses the PQ formula derived from the quadratic review to solve the transformed cubic equation, highlighting the connection between solving quadratic and cubic equations.
🤔 The script delves into complex analysis, discussing the implications of taking cube roots and the potential for multiple solutions, including complex numbers.
🌐 The concept of 'cube roots of unity' is introduced to generate additional solutions for the cubic equation, showing how multiplying the initial solution by these roots yields the other two solutions.
🔍 The video concludes with the complete derivation of the cubic formula, illustrating how to express the solutions in terms of the coefficients of the original cubic equation.
🎓 The final takeaway is the importance of understanding the underlying principles and techniques for solving polynomial equations, as demonstrated through the step-by-step process of deriving the cubic formula.

Q & A

What is the standard form of a quadratic equation?
-The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants and x represents the variable.
How does dividing the quadratic equation by 'a' simplify the process?
-Dividing the quadratic equation by 'a' simplifies the equation to x^2 + (b/a)x + (c/a) = 0, which eliminates the coefficient 'a' and allows us to use the PQ formula more easily.
What is the PQ formula in the context of solving quadratic equations?
-The PQ formula is a method to solve quadratic equations where 'P' is the new coefficient of x (b/a) and 'Q' is the constant term (c/a) after dividing the original equation by 'a'.
What is the purpose of completing the square in the given script?
-Completing the square is a technique used to solve quadratic equations by transforming them into a perfect square trinomial plus a constant, which can then be solved by taking the square root of both sides.
How does the substitution of x with y help in solving the quadratic equation?
-The substitution of x with y, and then adding a horizontal shift (k), helps in eliminating the x^1 term, which simplifies the equation to a form where the square root can be applied directly.
What is the significance of the horizontal shift (k) in the quadratic equation?
-The horizontal shift (k) is used to move the parabola left or right on the coordinate plane, which helps in eliminating the x term and transforming the equation into a form that is easier to solve.
What is the Cardano's method mentioned in the script for solving cubic equations?
-Cardano's method, also known as the cubic formula, is a technique for solving cubic equations of the form x^3 + px + q = 0 by transforming them into a quadratic equation in terms of z^3 and then solving for z.
What is the 'theater substitution' used for in the script?
-The 'theater substitution' is a specific substitution used in the context of solving cubic equations, where y is substituted with z minus some value, to transform the cubic equation into a quadratic form in terms of z^3.
How does the script connect the solution of quadratic equations to the solution of cubic equations?
-The script connects the solutions by first demonstrating the process of solving a quadratic equation and then using similar techniques, such as substitution and transformation, to solve a cubic equation.
What are the cube roots of unity mentioned in the script, and how are they used in solving cubic equations?
-The cube roots of unity are complex numbers that, when raised to the third power, equal one. They are used in solving cubic equations to find all possible solutions, especially when dealing with complex roots.

Outlines

00:00

📚 Solving Quadratic Equations as an Introduction

The script begins with a review of solving quadratic equations in standard form, ax^2 + bx + c = 0, by dividing through by 'a' to simplify and using the PQ formula. It introduces the concept of completing the square by graphing the equation and translating the parabola to eliminate the x term, resulting in a new equation y^2 = p^2/4 - q, from which the roots are derived as x = -b/2 ± sqrt(p^2/4 - q). This method is contrasted with the traditional approach and sets the stage for the cubic equation solution that follows.

05:08

🔍 Transitioning to Cubic Equations and Transformations

The script transitions from quadratic to cubic equations, discussing the goal of eliminating the x^2 term through a series of transformations. It introduces the substitution y = z - K to simplify the cubic equation into a form that resembles a quadratic equation in terms of z. The process involves careful manipulation of terms to achieve a solvable equation, emphasizing the importance of the substitution and the resulting equation as key steps towards solving cubic equations.

10:13

🔑 The Cardano/Substitution Method for Cubic Equations

This paragraph delves into the Cardano substitution, a method for solving cubic equations by transforming them into a quadratic form. The goal is to eliminate the x^2 term, leading to an equation in y that can be solved using the previously discussed quadratic formula. The script outlines the steps of this transformation, including the substitution y = z + K/z, and the algebraic manipulation required to achieve a quadratic equation in terms of z^3.

15:18

📉 Graphical Interpretation and Algebraic Manipulation

The script provides a detailed walkthrough of the algebraic steps involved in transforming the cubic equation using the Cardano substitution. It explains how to manipulate the equation to isolate y terms and how to combine like terms to simplify the equation further. The process involves distributing, factoring, and canceling terms to reach a simplified form that can be solved using the quadratic formula.

20:30

🧩 Solving the Resulting Quadratic Equation

After transforming the cubic equation into a quadratic form in terms of z, the script explains how to solve for z using the quadratic formula. It details the process of multiplying through by z^3 to clear the denominators and then applying the formula to find the roots of the equation. The explanation includes the algebraic simplification required to reach a solvable quadratic equation.

25:35

🤔 Considering Complex Solutions and the Nature of Cubic Equations

The script acknowledges the complexity of cubic equations and the potential for multiple solutions, including complex ones. It discusses the implications of taking cube roots and how this can lead to six possible solutions for z. However, it clarifies that for the purpose of finding y, the specific choice of z solution is less critical, as different choices will lead to equivalent results for y.

30:37

🌐 Introducing Cube Roots of Unity for Complete Solutions

To find all three roots of the cubic equation, the script introduces the concept of cube roots of unity, denoted as Omega. It explains how these roots, when multiplied with the solutions for z, yield all three solutions for y. The paragraph includes the derivation of the cube roots of unity and how they relate to each other, setting the stage for finding the complete set of solutions for the cubic equation.

35:39

🎯 Finalizing the Cubic Formula and Future Applications

The final paragraph wraps up the process by showing how to combine all the derived solutions into the final cubic formula. It hints at the practical applications of the cubic formula, teasing a future demonstration of how to use it to find the sine of 10 degrees. The script concludes by emphasizing the satisfaction of reaching the final solution and the comprehensive nature of the explanation provided.

Mindmap

Keywords

💡Cubic Equation

A cubic equation is a polynomial equation of degree three, typically written in the form ax^3 + bx^2 + cx + d = 0, where a, b, c, and d are constants, and x represents an unknown variable. In the video's context, the focus is on deriving and solving a cubic equation, demonstrating the process of eliminating higher-degree terms to simplify the equation to a solvable form.

💡Quadratic Equation

A quadratic equation is a second-degree polynomial equation in a single variable, with the general form ax^2 + bx + c = 0, where a, b, and c are constants, and a is not zero. The script begins by reviewing the solution to quadratic equations, which serves as a foundation for understanding the more complex cubic equations.

💡Standard Form

Standard form in algebra refers to the arrangement of terms in a polynomial so that the powers of the variable are in descending order. For instance, in the script, both quadratic and cubic equations are discussed in their standard forms, which is essential for applying solution methods like completing the square or the PQ formula.

💡PQ Formula

The PQ formula is a method used to solve quadratic equations once they have been simplified to the form x^2 + Px + Q = 0. It involves dividing through by 'a' to get the equation in a form where the coefficients of x^2 and the constant term are P and Q, respectively. The script mentions this formula as a precursor to the more complex cubic formula derivation.

💡Completing the Square

Completing the square is a technique used to solve quadratic equations by transforming the equation into a perfect square trinomial plus a constant, which can then be solved by taking the square root of both sides. The script discusses an alternative to this method by graphing and translating the parabola to eliminate the x term.

💡Theater Substitution

The Theater substitution, also known as the Tschirnhaus transformation, is a method used to simplify the solution of cubic equations by reducing them to a quadratic form. In the script, this substitution is applied to transform the cubic equation into a form that can be solved using the PQ formula, illustrating its utility in solving higher-degree polynomials.

💡Cube Root

The cube root of a number is a value that, when multiplied by itself three times, gives the original number. The script discusses taking the cube root of both sides of an equation to simplify the process of solving for the variable, particularly in the context of finding the solutions to the cubic equation.

💡Unity

In the context of the script, 'unity' refers to the number 1, specifically when discussing the cube roots of unity. These are complex numbers that, when raised to the power of three, equal one. The cube roots of unity are used in the script to find all possible solutions to the cubic equation.

💡Complex Numbers

Complex numbers are numbers that consist of a real part and an imaginary part, usually written in the form a + bi, where 'i' is the imaginary unit with the property that i^2 = -1. The script mentions complex numbers in the context of solving cubic equations, particularly when considering the cube roots of unity.

💡Polar Form

Polar form is a way of representing complex numbers based on their magnitude (distance from the origin) and angle (direction from the positive real axis). The script briefly touches on converting complex numbers to polar form to simplify calculations, specifically when dealing with the cube roots of unity.

💡Conjugate

In mathematics, a conjugate of a complex number is obtained by changing the sign of the imaginary part while keeping the real part the same. The script uses the concept of conjugates to simplify expressions involving complex numbers, particularly when multiplying top and bottom by the conjugate to remove the imaginary unit 'i'.

Highlights

Introduction to deriving the cubic formula by first reviewing the solution of a quadratic equation.

Transformation of the standard form quadratic equation by dividing by 'a' and introducing variables p and q.

Explanation of the process to eliminate the linear term in the quadratic equation by horizontal translation.

Graphical representation of the parabola and the effect of horizontal translation on the equation.

Substitution method to eliminate the first power term in the quadratic equation, leading to a perfect square.

Derivation of the PQ formula for quadratic equations using the completed square method.

Transition to cubic equations and the challenge of eliminating higher power terms.

Introduction of the Tschirnhaus substitution for transforming cubic equations into a solvable form.

Guideline for the transformation process to eliminate the quadratic term in the cubic equation.

Substitution of y for x and the addition of a variable k to facilitate the elimination of the quadratic term.

Detailed algebraic manipulation to derive a quadratic equation from the transformed cubic equation.

Use of the PQ formula to solve the derived quadratic equation in terms of z.

Complex analysis involved in solving the cubic equation and the introduction of cube roots.

Explanation of the cube root of unity and its role in finding all solutions to the cubic equation.

Final steps to combine all parts of the solution and express the roots in terms of the original coefficients.

Presentation of all three roots of the cubic equation derived from the completed process.

Discussion on the practical applications and the significance of the derived cubic formula.

Transcripts

Browse More Related Video

[Algebra] Is there any cubic formula?

How To Find The Real & Imaginary Solutions of Polynomial Equations

Calculus grade 12: Exam

EXTREME quintic equation! (very tiring)

Solving Quadratics by Using the Quadratic Formula

Solving Polynomial Equations By Factoring and Using Synthetic Division

Related Tags

Cubic Formula Mathematics Quadratic Equation PQ Formula Theater Substitution Roots of Unity Educational Content Math Tutorial Solving Equations Algebraic Methods