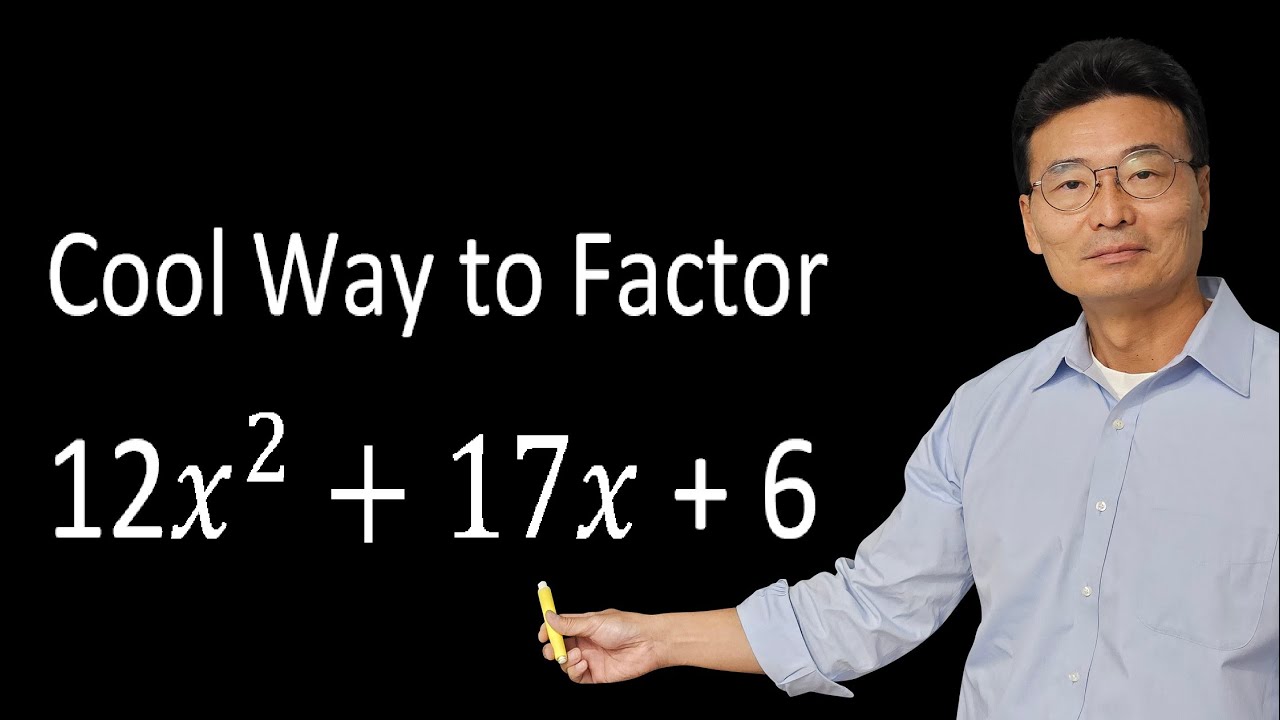algebra tutorial: factoring a quartic trinomial vs a quadratic trinomials
TLDRIn this educational video, the presenter explores the factorability of two algebraic expressions that appear similar but differ in their powers. The audience is challenged to determine which is factorable. The presenter explains that one expression cannot be factored due to the impossibility of combining terms using rational numbers. The other expression, despite its different powers, is factorable through a process of grouping and recognizing patterns, ultimately leading to a factored form that includes a perfect square and a difference of squares. The video aims to engage viewers in the intricacies of algebraic factoring.
Takeaways
- 🔍 The video discusses the factorability of algebraic expressions, emphasizing that even similar-looking expressions may have different factorability.
- 📚 The presenter invites viewers to pause and try factoring two given algebraic expressions before revealing the answer.
- 🚫 One of the expressions is not factorable, while the other is, highlighting the importance of recognizing patterns in algebraic expressions.
- 🔢 The expressions involve powers of 'x' and real numbers, with the presenter focusing on the factorability of quadratic and higher powers.
- ❌ The first expression is deemed non-factorable after attempting to break down the numbers 9 and 49 using rational numbers.
- 📉 The presenter explains that the non-factorable expression cannot be broken down into simpler factors, despite initial attempts.
- 📈 The second expression, despite having different powers, is factorable, and the presenter suggests thinking about alternative approaches to factor it.
- 🤔 The presenter uses trial and error to explore different combinations of factors, illustrating the process of factoring algebraic expressions.
- 🔄 The video emphasizes the importance of recognizing when an expression can be factored by grouping and using perfect square patterns.
- 📝 The presenter writes down the steps and thought process, showing how to transform the original expression into a factorable form.
- 🎯 The final takeaway is the successful factoring of the second expression using a combination of grouping and recognizing perfect square differences.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is factoring algebraic expressions, specifically focusing on the factorability of two similar-looking expressions with different powers.
Why does the script suggest pausing the video?
-The script suggests pausing the video to allow viewers to attempt the factoring problems themselves before revealing the solution.
What is the difference between the two expressions presented in the script?
-The difference between the two expressions is the powers of the variables. While they look similar, one expression is factorable, and the other is not.
Why is the first expression not factorable according to the script?
-The first expression is not factorable because, despite trying different combinations of real numbers to factor it, it does not break down into a product of simpler expressions.
What is the strategy used to determine if an expression is factorable?
-The strategy involves attempting to break down the expression into a product of simpler expressions using real numbers, specifically looking for pairs that multiply to give the constant terms and add up to the coefficients of the variable terms.
What is the second expression's fate in terms of factorability?
-The second expression is factorable, but it requires a different approach and understanding of patterns to successfully factor it.
What is the significance of the 'heart of one' in the script?
-The 'heart of one' seems to be a metaphor used by the speaker to describe the core or the key part of the problem-solving process, particularly in making the connection between the original problem and an easier version.
How does the script suggest making the connection between the original and an easier version of the problem?
-The script suggests making the connection by identifying patterns and similarities between the original problem and a simplified version, then using those insights to solve the original problem.
What is the method used to factor the second expression in the script?
-The method involves grouping terms and using the difference of squares pattern to factor the expression into a product of simpler expressions.
What is the final factored form of the second expression according to the script?
-The final factored form of the second expression is (x + 3)(x + 3)(x - 1), which is derived by recognizing and applying the difference of squares pattern.
How does the script conclude the discussion on factoring?
-The script concludes by successfully factoring the second expression and emphasizing the importance of recognizing patterns and applying algebraic strategies to solve problems.
Outlines
🧐 Factoring Challenges in Algebra
This paragraph discusses the intricacies of factoring algebraic expressions, particularly focusing on two seemingly similar problems with different outcomes. The speaker encourages viewers to pause and attempt the problems before revealing that only one is factorable. The non-factorable problem is identified due to the impossibility of breaking down the given numbers into a combination that would result in the original expression. The speaker also explains the importance of recognizing patterns and the limitations of certain algebraic identities in factoring.
📚 Mastering Factoring Through Grouping and Perfect Squares
The second paragraph delves into the process of factoring a trinomial by grouping and identifying perfect squares. The speaker illustrates a step-by-step approach to factor the given expression, which includes recognizing the pattern of a perfect square and applying the difference of squares formula. The summary highlights the method of grouping terms to simplify the expression and the successful factoring of the trinomial into a product of binomials, showcasing the beauty and logic behind algebraic manipulation.
Mindmap
Keywords
💡Intercourse
💡Patterns
💡Algebra
💡Factoring
💡Powers
💡Multinomial
💡Rational Numbers
💡Trinomial
💡Grouping
💡Perfect Square
💡Difference of Squares
Highlights
The presenter introduces two similar algebra factoring questions, suggesting that only one is factorable.
The challenge is to determine which of the two questions is factorable and why.
The presenter explains that a square multinomial must have even powers of x.
The first question is deemed not factorable due to the impossibility of breaking down 9 and 49 into factors that include x squared.
The second question is factorable despite the different powers, indicating a deeper analysis is needed.
The presenter attempts to factor the second question by opening two parentheses but finds it doesn't work as expected.
A crucial step is introduced where the presenter considers a modified version of the original question for easier factoring.
The presenter shows how to connect the easier version back to the original question through a series of transformations.
Grouping is used as a technique to factor the second question into a perfect square and a difference of squares.
The presenter demonstrates the factoring process step by step, emphasizing the importance of recognizing patterns.
The final factored form of the second question is revealed, showcasing the successful application of algebraic techniques.
The presenter emphasizes the importance of not giving up on challenging algebra problems and finding creative solutions.
A summary of the thought process and the steps taken to solve the factoring problem is provided.
The presenter concludes by highlighting the satisfaction and educational value of solving algebraic problems.
The video ends with a reminder of the joy of algebra, encouraging viewers to appreciate the beauty of mathematical problem-solving.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: