Finding Z Critical Values for a Given Confidence Level using the TI84

Dr. Roty's Tutorial Channel
26 Oct 201506:41
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Dr. Roadie demonstrates how to use a TI-84 calculator to find a critical value for a given confidence level. The concept is simplified by explaining that it's essentially finding a percentile using the inverse normal function. The video focuses on calculating for a 95% confidence interval, illustrating how to determine the 97.5 percentile, which corresponds to the area in the standard normal distribution. Dr. Roadie suggests visualizing the problem on paper for clarity and then guides viewers through the calculator steps, emphasizing the importance of setting the correct parameters for the mean and standard deviation. The final step yields a critical value of 1.96, rounded to two decimals, providing a practical example of statistical analysis using a common calculator.

Takeaways
  • 📚 The video is a tutorial by Dr. Roadie on using a TI-84 calculator to find a critical value for a given confidence level.
  • 🔍 The process involves finding a percentile in the standard normal distribution (mean = 0, standard deviation = 1).
  • 📈 The critical value is the point on the normal distribution curve that corresponds to a certain percentage of the area under the curve.
  • 🌐 For a 95% confidence interval, 95% of the probability lies between two limits, with 2.5% in each tail of the distribution.
  • 📝 The significance level (alpha) is related to the confidence level and is calculated as 1 - confidence level.
  • 📉 To find the critical value, calculate the percentile corresponding to the area in the tail of the distribution, which is (1 - alpha/2) * 100.
  • 📝 For a 95% confidence interval, alpha is 0.05, and the percentile to find is 97.5%.
  • 🎨 A visual approach is suggested by sketching the normal distribution curve and identifying the required percentile.
  • 🔢 The TI-84 calculator's inverse normal function is used to find the critical value, accessed through the '2nd', 'Vars', 'Distribution', and then selecting '3:invNorm'.
  • ⚙️ Ensure the calculator is set to a mean of 0 and a standard deviation of 1 for the standard normal distribution.
  • 📊 The calculator will provide the critical value, which for a 95% confidence interval is approximately 1.96 when rounded to two decimal places.
Q & A

  • What is the main topic of the video by Dr. Roadie?

    -The main topic of the video is to demonstrate how to use a TI-84 calculator to find a critical value for a given confidence level.

  • Why might the notation in the video seem complicated?

    -The notation might seem complicated because it involves statistical terms and concepts, but the essence of the task is to find a percentile using the inverse normal function.

  • What is a critical value in the context of this video?

    -A critical value is the value in the standard normal distribution (mean = 0, standard deviation = 1) that will give you a certain percentage surrounding the center, which corresponds to the desired confidence level.

  • What is the significance of the 95% confidence interval in the video?

    -A 95% confidence interval means that 95% of the probability of the normal curve is between the two limits, with the remaining 5% split equally into the two tails of the distribution.

  • How much of the total area under the normal curve is represented by the red areas (tails) in a 95% confidence interval?

    -In a 95% confidence interval, the red areas (tails) represent 5% of the total area, with each tail having 2.5% or 0.025 as a decimal.

  • What is the Z alpha over two in the context of finding a critical value?

    -Z alpha over two refers to the critical value that corresponds to the area in the tail of the normal distribution, which is used to find the percentile associated with the desired confidence level.

  • How can you determine the percentile needed for a given confidence level without a calculator?

    -You can determine the percentile needed by visualizing the normal distribution and calculating the area to the left of the tail that corresponds to the (1 - alpha/2) * 100%, where alpha is the significance level.

  • What is the significance level (alpha) in relation to the confidence level?

    -The significance level (alpha) is related to the confidence level in that alpha is equal to 1 minus the confidence level. It represents the probability of the tails in the normal distribution.

  • How does Dr. Roadie suggest finding the percentile needed for the critical value?

    -Dr. Roadie suggests visualizing the normal distribution, sketching it out on paper, and performing simple subtraction to find the percentile needed for the critical value.

  • What function on the TI-84 calculator is used to find the critical value?

    -The inverse normal function on the TI-84 calculator is used to find the critical value by entering the desired area as a decimal and setting the mean to 0 and the standard deviation to 1.

  • What is the critical value found in the video for a 95% confidence interval, rounded to two decimals?

    -The critical value found in the video for a 95% confidence interval, rounded to two decimals, is 1.96.

Outlines
00:00
📚 Understanding Confidence Intervals and Critical Values

Dr. Roadie introduces the concept of finding a critical value for a given confidence level using a TI-84 calculator. He simplifies the process by explaining that it's essentially finding a percentile from the standard normal distribution. The video focuses on a 95% confidence interval, illustrating how to determine the critical value by calculating the area under the normal curve. Dr. Roadie emphasizes that the normal curve is symmetric, and for a 95% confidence interval, 95% of the data lies within the interval with 2.5% in each tail. He explains that the critical value corresponds to the 97.5 percentile, which can be found using the inverse normal function on the calculator. He suggests visualizing the problem by sketching the normal distribution and identifying the required percentile, which in this case is 97.5%. The significance level, or alpha, is also discussed, relating it to the confidence level as 1 minus the confidence level.

05:01
🔢 Using the TI-84 Calculator to Find Critical Values

In this section, Dr. Roadie demonstrates how to use the TI-84 calculator to find the critical value for a 95% confidence interval. He instructs viewers to use the inverse normal function, which is accessed by navigating to the 'distribution' menu and selecting the 'inverse normal' option. The calculator is set to a standard normal distribution with a mean of 0 and a standard deviation of 1. The area to the left of the critical value, which corresponds to the desired percentile (97.5% in this case), is entered as a decimal (0.975). Dr. Roadie ensures that the calculator is set to the correct parameters and then calculates the critical value, which is approximately 1.96 when rounded to two decimal places. This step-by-step guide provides a clear method for finding critical values using the TI-84 calculator, making it accessible for those learning statistical concepts.

Mindmap
Keywords
💡TI-84 Calculator
The TI-84 Calculator is a graphing calculator used widely in mathematics and science education. In the context of the video, it serves as the primary tool for finding critical values for statistical analysis. The script demonstrates how to use the calculator to determine a critical value for a given confidence level, which is a common task in statistics.
💡Critical Value
A critical value is a specific value from a statistical distribution that is used to determine whether to reject a null hypothesis. In the script, the critical value is the value on the standard normal distribution that corresponds to a certain confidence interval, which is essential for hypothesis testing.
💡Confidence Level
The confidence level is a measure of the accuracy of an estimate. It represents the percentage of possible confidence intervals that contain the true value. In the video, the speaker is explaining how to find a critical value for a 95% confidence interval, which is a common level used in statistical analysis.
💡Percentile
A percentile is a value below which a given percentage of observations in a group of observations falls. In the video, the speaker discusses finding the percentile that corresponds to the critical value, which is crucial for determining the confidence interval.
💡Normal Distribution
The normal distribution, also known as Gaussian distribution, is a probability distribution that is important in statistics. In the script, the normal distribution is referenced as the standard normal distribution with a mean of 0 and a standard deviation of 1, which is used to find the critical value.
💡Standard Normal Distribution
A standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1. It is used in the video to find the critical value for a given confidence level, as it provides a common scale for comparing different sets of data.
💡Inverse Normal Function
The inverse normal function, also known as the quantile function, is used to find the value of a random variable corresponding to a given probability. In the video, the speaker uses the inverse normal function on the TI-84 calculator to find the critical value corresponding to a 97.5 percentile.
💡Significance Level (Alpha)
The significance level, denoted by alpha, is the probability of rejecting the null hypothesis when it is true. In the script, alpha is calculated as 1 minus the confidence level, and it is used to determine the critical value for the confidence interval.
💡Z-Score
A Z-score represents the number of standard deviations an element is from the mean. In the context of the video, the critical value is essentially a Z-score that corresponds to the desired percentile in the standard normal distribution.
💡Hypothesis Testing
Hypothesis testing is a statistical method used to make decisions about populations based on sample data. The critical value, as discussed in the video, plays a key role in hypothesis testing by helping to determine whether the null hypothesis should be rejected.
Highlights

Introduction to using a TI-84 calculator to find critical values for a given confidence level.

Explanation that finding a critical value involves identifying a specific percentile.

Clarification that the critical value is found in the standard normal distribution (mean = 0, standard deviation = 1).

Illustration of a 95% confidence interval and its relation to the normal distribution curve.

Description of the symmetry in the normal distribution and how it affects the tails.

Calculation of the area in the tails for a 95% confidence interval (2.5% in each tail).

Explanation of how to find the Z value for the upper tail (Z alpha over two).

Introduction of the concept of alpha as the significance level related to the confidence level.

Demonstration of calculating alpha by subtracting the confidence level from 1.

Conversion of alpha to find the percentile needed for the critical value (97.5th percentile).

Suggestion to visualize the process with a sketch for easier understanding.

Introduction to using the inverse normal function on the TI-84 calculator.

Instructions on navigating the calculator's menu to access the inverse normal function.

Guidance on entering the correct values for the mean and standard deviation in the calculator.

Step-by-step process of inputting the area as a decimal and calculating the critical value.

Final calculation of the critical value to two decimal places (1.96).

Summary of how to find a critical value for a given confidence level using the TI calculator.

Transcripts

Browse More Related Video

Normal Distribution: Calculating Quantiles {TI 84 Plus CE}

Find Critical Value Za/2 with Statcrunch

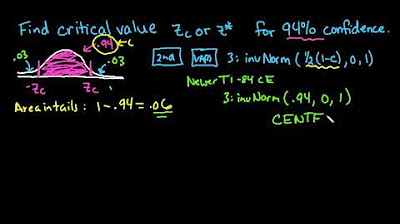
Find Critical Value Z for Confidence Intervals with TI-84

7.1.3 Estimating a Population Proportion - Critical Values, Rationale and How to Compute Them

Find the z-score given the confidence level

7.2.5 Estimating a Population Mean - Confidence Intervals with Known Pop. Standard Deviation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TI-84 CalculatorCritical ValueConfidence LevelStatistical AnalysisEducational VideoNormal DistributionInverse NormalPercentilesData AnalysisTutorial