Find Critical Value Z for Confidence Intervals with TI-84

Math and Stats Help
24 Mar 201904:36
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video demonstrates how to calculate critical values for a 94% confidence interval using the TI-84 graphing calculator. It begins by explaining the concept of critical values and their significance in capturing a specific percentage of samples within the normal distribution curve. The video then proceeds to show two methods for finding these values: one for the newer TI-84 Color Edition and another for older models. The presenter guides viewers through the calculator's interface, illustrating the steps to input the necessary parameters and retrieve the critical values, which in this case are -1.88 and 1.88. The video concludes with an invitation for viewers to ask questions or request additional topics.

Takeaways
  • 📚 The video is a tutorial on finding critical values for a 94% confidence interval using the TI-84 graphing calculator.
  • 📈 The critical values are the points on the normal curve that define the endpoints of the confidence interval.
  • 🔍 The goal is to capture 94% of the samples within the curve, leaving 6% in the tails.
  • 📊 The area in the middle of the curve represents the level of confidence, which is 0.94 in this case.
  • 🔢 To find the critical values, the calculator's inverse norm function is used, which calculates the z-score corresponding to the given confidence level.
  • 📱 For older TI-84 models, the user inputs 1/2, 1 minus the confidence level, and 0, 1 to find the area in the tails.
  • 💻 On newer TI-84 Color Edition calculators, there's an option to select 'Center' which simplifies the process.
  • 👉 The video demonstrates both methods: the older method and the newer method with the 'Center' option.
  • 📉 The critical values for a 94% confidence interval are found to be -1.88 and +1.88.
  • 📝 Typically, only the positive z-score is reported as the critical value for the confidence interval.
  • ❓ The video encourages viewers to ask questions or request additional topics for future tutorials.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is demonstrating how to find critical values zc or z* for a 94% confidence interval using a TI-84 graphing calculator.

  • What is the purpose of finding critical values in a normal curve?

    -The purpose of finding critical values is to determine the values that end the confidence interval, ensuring that a certain percentage (in this case, 94%) of the samples are captured within the curve.

  • What does a 94% confidence interval mean in terms of the normal curve?

    -A 94% confidence interval means that 94% of the area under the normal curve is within the interval, with 3% in each tail (0.06 total, divided by 2).

  • How does the video guide the viewer to find the critical values using the TI-84 calculator?

    -The video provides step-by-step instructions on using the inverse norm function on the TI-84 calculator, with options for both older and newer models.

  • What is the difference between using the inverse norm function on an older TI-84 and the newer TI-84 Color Edition?

    -The older TI-84 requires entering 1/2, 1 minus the level of confidence, and 0, 1, while the newer TI-84 Color Edition has a 'Center' option that simplifies the process by allowing you to input the level of confidence directly.

  • What is the critical z value for a 94% confidence interval according to the video?

    -The critical z values for a 94% confidence interval are -1.88 and +1.88, as demonstrated on the TI-84 calculator.

  • Why are both positive and negative z scores important for the confidence interval?

    -Both positive and negative z scores are important because they represent the symmetrical endpoints of the confidence interval on a normal curve.

  • How does the video handle the symmetry of the normal curve when finding critical values?

    -The video acknowledges the symmetry by showing that if the negative z score is -1.88, then the positive z score is +1.88, and only the positive value is typically reported.

  • What is the significance of the area in the tails of the normal curve in this context?

    -The area in the tails of the normal curve represents the remaining percentage of the data that falls outside the confidence interval, which in this case is 6% (0.06), divided equally between the two tails.

  • How can viewers get help if they have questions or need additional topics covered?

    -Viewers can ask questions or request additional topics by reaching out to the video creator, as suggested at the end of the video.

Outlines
00:00
📊 Finding Critical Values for 94% Confidence on TI-84 Calculator

This paragraph introduces the video's objective, which is to demonstrate how to calculate the critical value zc or z star for a 94% confidence interval using a TI-84 graphing calculator. The presenter emphasizes the importance of visualizing the process by explaining the concept of a normal curve and its critical values, which define the endpoints of the confidence interval. The goal is to capture 94% of the samples within the curve, with the remaining 6% (0.06) distributed equally in the two tails. The video will show two methods to find these critical values using the calculator's inverse norm function, one for older TI-84 models and another for the newer TI-84 Color Edition, which includes a 'Center' option.

Mindmap
Keywords
💡Critical Value
A critical value, denoted as zc or z* in the script, is a specific z-score on the standard normal distribution that corresponds to the cutoff point for a given confidence interval. In the context of the video, the critical value is crucial for determining the endpoints of a 94% confidence interval, which means that 94% of the data is expected to lie within this interval. The script illustrates how to find this critical value using a TI-84 graphing calculator, which is essential for statistical analysis.
💡Confidence Interval
A confidence interval is a range of values, derived from a statistical model, that is likely to contain the value of an unknown parameter. The video focuses on calculating a 94% confidence interval, which implies that there is a 94% probability that the interval contains the true population parameter. The critical values are the endpoints of this interval, and the script demonstrates how to find them using a calculator.
💡Normal Curve
The normal curve, also known as the Gaussian curve or bell curve, is a fundamental concept in statistics that represents the distribution of a variable that clusters around the mean, with the shape of the curve indicating how data points are distributed. In the video, the normal curve is used to visualize the distribution of sample data and to identify the critical values that define the 94% confidence interval.
💡Z Score
A z score is a standard score that indicates how many standard deviations an element is from the mean. In the script, the z score is used to find the critical values that correspond to the tails of the normal distribution outside the 94% confidence interval. The video explains that the positive and negative z scores are symmetrical and are used to determine the endpoints of the interval.
💡TI-84 Graphing Calculator
The TI-84 graphing calculator is a popular tool used for mathematical and statistical calculations. The script provides a tutorial on how to use this calculator to find the critical value for a 94% confidence interval. It mentions different methods for older and newer models of the calculator, showing how to input values and navigate the calculator's functions.
💡Inverse Norm
The inverse norm, or inverse normal distribution function, is used to find the value (z score) that corresponds to a given probability in the standard normal distribution. In the video, the inverse norm function on the TI-84 calculator is used to calculate the critical z score for the 94% confidence interval. This function is crucial for determining the endpoints of the interval.
💡Area in the Middle
The term 'area in the middle' refers to the proportion of the data that falls within the confidence interval on the normal curve. In the script, it is stated that the goal is to capture 94% of the samples, which means that 94% of the area under the normal curve is within the interval. This area is central to understanding confidence intervals and their significance.
💡Area in the Outside Tails
The 'area in the outside tails' is the portion of the data that falls outside the confidence interval. In the context of the video, after accounting for the 94% area in the middle, the remaining 6% is split equally between the two tails of the normal distribution, with 3% in each tail. The critical values are found by determining the z scores that correspond to these tail areas.
💡Level of Confidence
The level of confidence, mentioned as 0.94 in the script, is a measure of how certain we are that the true population parameter lies within the calculated confidence interval. The video demonstrates how to input this level of confidence into the TI-84 calculator to find the corresponding critical values for the 94% confidence interval.
💡Symmetry
Symmetry in the context of the normal distribution refers to the mirror-image reflection of the curve around the mean. The script explains that because the normal distribution is symmetrical, if one critical value is negative 1.88, the corresponding value on the other side of the distribution is positive 1.88. This symmetry is key to understanding how to find both critical values.
Highlights

The video demonstrates how to find a critical value zc or z star for a 94% confidence interval.

The process is explained using a TI-84 graphing calculator.

Critical values are the endpoints of the confidence interval on a normal curve.

A 94% confidence interval captures 94% of the samples in the normal curve.

The z score corresponding to the positive and negative endpoints for 94% confidence is sought.

The area outside the 94% confidence interval is calculated as 1 minus 0.94, resulting in 0.06.

The area in each tail is half of the total area outside the confidence interval, which is 0.03.

For older TI-84 calculators, the inverse norm function is accessed by pressing 2nd and Vars.

Input 1/2, 1 minus the level of confidence, and 0, 1 for the inverse norm function on older calculators.

The area in the tail is divided by 2 to find the area in each tail.

Newer TI-84 Color Edition calculators have a new feature for the inverse norm function.

On newer calculators, input the level of confidence, 0, 1, and select Center for the inverse norm.

The calculator provides the critical values that end the 94% area in the middle.

The critical values for a 94% confidence interval are -1.88 and 1.88.

Most calculators will provide only the negative critical value due to symmetry.

The positive z score of 1.88 is typically reported as the critical value for the confidence interval.

The critical value of 1.88 is the value that ends the confidence interval.

The video concludes with an invitation for viewers to ask questions or request additional topics.

Transcripts

Browse More Related Video

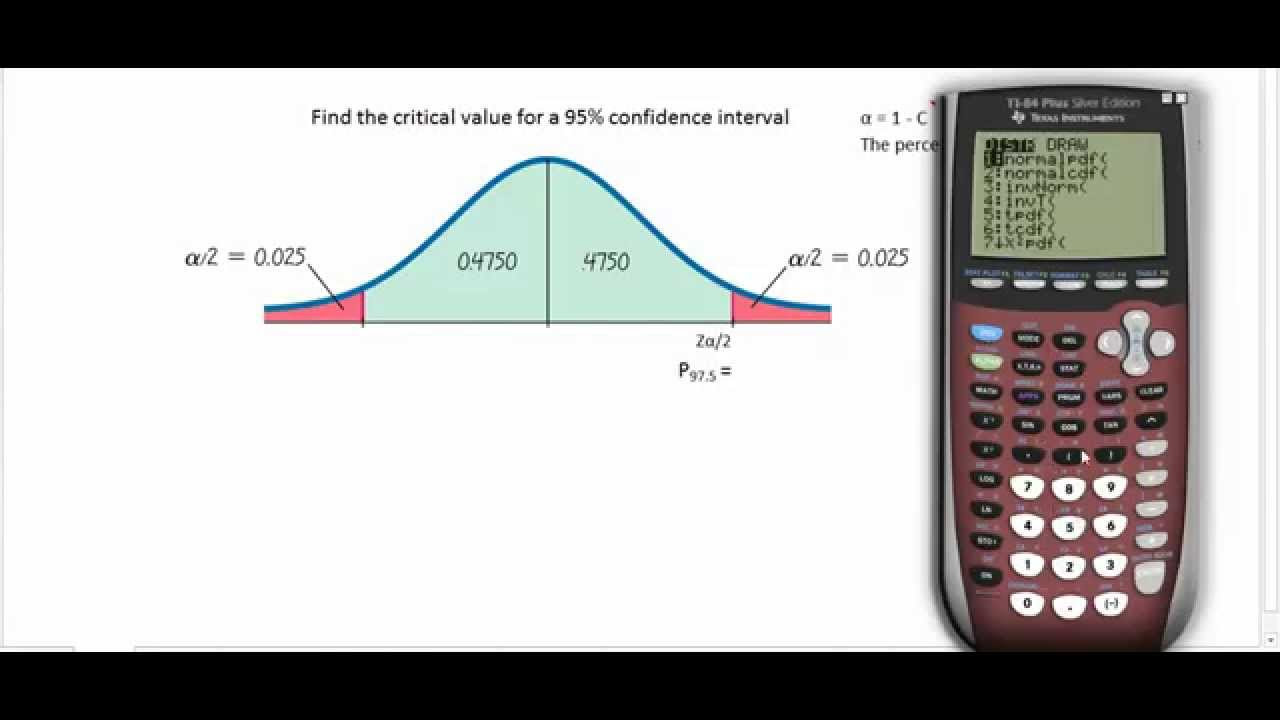
Finding Z Critical Values for a Given Confidence Level using the TI84

TI-84 Plus Graphing Calculator Guide: Statistics

How to Solve Systems of Equations on TI-84 Plus CE and TI-84 Plus Silver Edition

Probabilities in a Normal Distribution - TI-84

Finding Limits Numerically with a TI-84 Calculator

Calculus - Finding the derivative at a point using a Ti-83 or 84 calcululator

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Confidence IntervalStatistical AnalysisTI-84Calculator TutorialZ ScoreCritical ValueData ScienceEducational ContentMathematicsTutorial Video