Lecture 22: Fields of Arrows Differential Equations
TLDRThis video script explores the power of mathematics and calculus through the lens of differential equations, which are central to understanding and predicting various phenomena in science and beyond. It begins with a practical example of calculating compound interest in a savings account, illustrating how differential equations relate to real-world problems. The script then delves into the history of differential equations, highlighting the contributions of Newton, Leibniz, and others. It discusses their applications in physics, such as modeling the motion of falling objects and pendulums, and introduces the concept of direction fields for visualizing solutions. The video also examines population growth models, including Malthus's exponential growth and the refined logistic model, which incorporates carrying capacity and threshold effects. The script concludes by emphasizing the broad applicability of differential equations in diverse fields and hints at upcoming topics like predator-prey dynamics and musical instruments.
Takeaways
- 📚 Mathematics and calculus are powerful tools for understanding and manipulating the world through mathematical models.
- 💰 An example provided is calculating the growth of money in a savings account with continuous compounding, illustrating the use of mathematical functions to predict future states.
- 📈 The concept of the derivative is central to understanding rates of change, such as interest rates in savings accounts, and is foundational in formulating differential equations.
- 🔍 The script explains that differential equations relate the rate of change of an unknown function to the function itself, and solving them involves finding the function that satisfies the relationship.
- 📉 The application of differential equations extends to various fields including physics, biology, economics, and social sciences, highlighting their broad utility.
- 🧭 Historically, Newton and Leibniz were pioneers in formulating differential equations, marking a significant advancement in calculus.
- 🪢 The Bernoulli family and other mathematicians like Lagrange and Laplace contributed significantly to the development and solution methods of differential equations.
- 📊 The script introduces the concept of direction fields as a method to visualize and approximate solutions to differential equations without explicitly solving them.
- 🌱 Malthus's model of population growth is presented as an exponential growth model, which is simple yet unrealistic for long-term predictions due to unlimited growth implications.
- 🌿 The Verhulst model, or logistic equation, is introduced as a refined population growth model that includes a carrying capacity to account for limited resources, offering a more realistic approach.
- 🚫 The threshold model in population growth is mentioned, emphasizing that populations below a certain size will decline instead of grow, adding another layer of realism to population models.
Q & A
What are mathematical models and why are they important in understanding the world?
-Mathematical models are constructs that represent some aspect of the world through mathematical relationships. They are important because they allow us to describe or predict features of the world, making it possible to understand and manipulate complex phenomena in various fields such as economics, physics, and biology.
Can you explain the concept of continuous compounding in the context of a savings account?
-Continuous compounding refers to the process where interest is added to the principal continually over time, rather than at fixed intervals. In the context of a savings account, continuous compounding means that the interest earned is reinvested instantly, allowing the account balance to grow at a faster rate compared to simple interest or discrete compounding.
What information does the interest rate of a savings account provide, and how is it related to derivatives?
-The interest rate of a savings account provides information about the rate at which the money in the account is expected to grow. This rate of change is related to derivatives in calculus, as the derivative of a function represents the rate of change of that function. In this case, the derivative represents the rate at which the account balance is increasing over time.
How does the concept of a derivative relate to the rate of change in real-world scenarios?
-In real-world scenarios, the concept of a derivative is directly related to the rate of change of a quantity with respect to another. For example, in the context of a savings account, the derivative represents the rate at which the account balance changes over time, which is influenced by the interest rate.
What is a differential equation and why are they significant in various fields of study?
-A differential equation is an equation that relates a function with its derivatives. They are significant in various fields of study because they describe the rate at which a process changes. Differential equations are used to model a wide range of phenomena in physics, biology, economics, and engineering, among others.
How does the concept of a differential equation apply to the motion of a falling object?
-The motion of a falling object can be described by a differential equation that relates the object's position, velocity, and acceleration. For instance, the acceleration due to gravity can be represented as the second derivative of the position function with respect to time, which is a constant value representing the acceleration of the object.
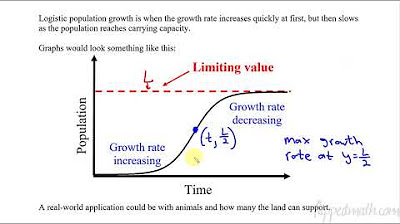
What is the significance of the carrying capacity in population growth models?
-The carrying capacity, denoted as 'k' in population growth models, represents the maximum population size that an environment can sustain indefinitely. It is significant because it introduces a limit to population growth, reflecting the fact that resources are finite and population growth cannot continue indefinitely.
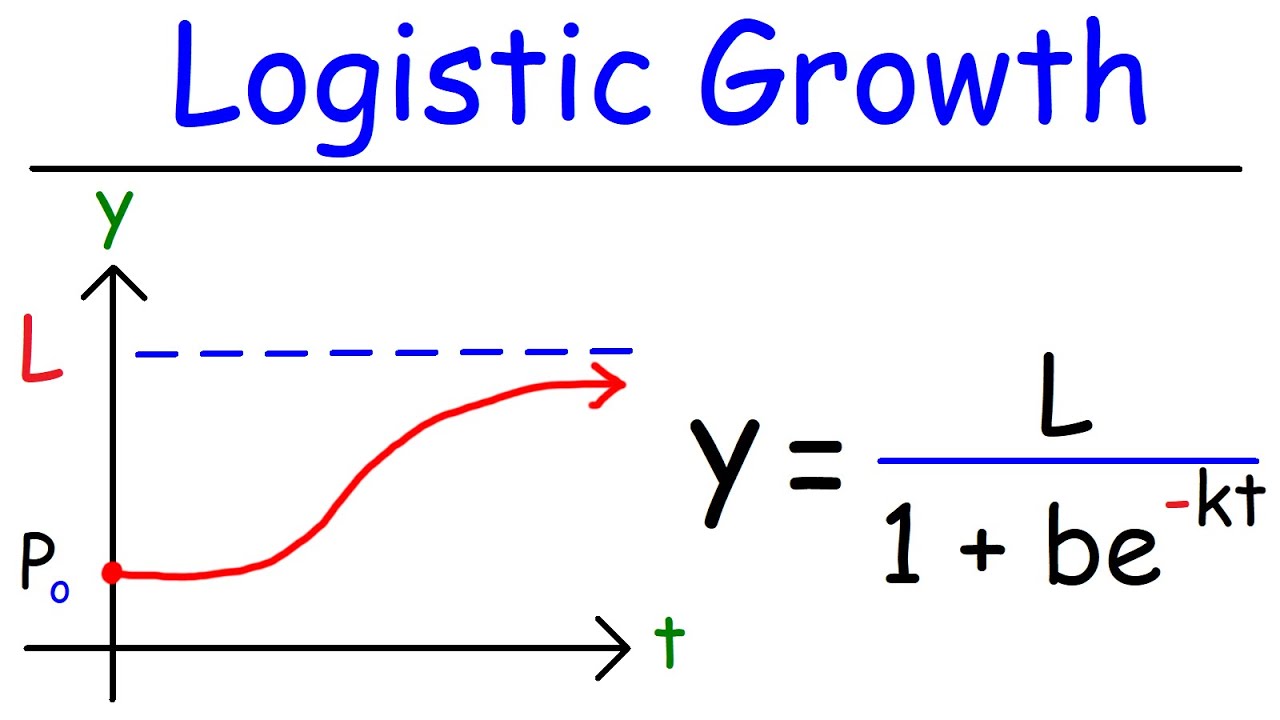
How does the logistic equation or the Verhulst model refine the Malthusian model of population growth?
-The logistic equation, also known as the Verhulst model, refines the Malthusian model by introducing a carrying capacity. It adjusts the growth rate based on the current population size relative to the carrying capacity, slowing down the growth as the population approaches the carrying capacity, thus preventing unlimited exponential growth.
What is the role of initial conditions in solving differential equations?
-Initial conditions are essential in solving differential equations because they provide specific values that the solution must satisfy at a given point. Knowing the initial conditions allows us to determine a unique solution from a family of solutions, which is particularly important in initial value problems.
How can direction fields be used to analyze the solutions of differential equations?
-Direction fields, also known as phase diagrams, can be used to visualize the solutions of differential equations. At each point in the field, an arrow indicates the slope of the tangent line to the solution curve, which is derived from the differential equation. By following these arrows, one can sketch the trajectory of the solution, providing a qualitative understanding of the behavior of the system described by the differential equation.
What is the historical significance of Newton and Leibniz in the development of differential equations?
-Newton and Leibniz are historically significant as they were the first to write down differential equations. They are credited with inventing the notation for derivatives, which laid the foundation for the field of calculus and the study of differential equations.
Outlines
📚 Introduction to Mathematical Modeling and Calculus
This paragraph introduces the power of mathematics and calculus as tools for understanding and manipulating the world through mathematical models. It uses the example of calculating the growth of money in a savings account with continuous compounding interest to illustrate how mathematical functions can represent real-world phenomena. The paragraph explains that the interest rate given by a savings account is a piece of information about the rate of change, which is captured by the derivative in calculus. The focus is on understanding the relationship between the amount of money in the account and its rate of change over time.
🔍 Differential Equations: The Language of Change
This section delves into differential equations, which are equations relating a function to its derivatives. The paragraph explains that solving a differential equation involves finding a function that satisfies the given relationship, rather than finding a single number. It provides an example of a simple differential equation representing money growing in a savings account and extends the discussion to the broader applications of differential equations in various scientific fields. The historical context is given, mentioning Newton and Leibniz as pioneers in the development of calculus and differential equations, and their importance in describing phenomena across physics, biology, economics, and social sciences.
📉 Applications of Differential Equations in Physics
This paragraph explores the application of differential equations in physics, starting with the example of a falling object and its acceleration due to gravity. It explains how the rate of falling is described by a differential equation relating the velocity (the derivative of position) to time. The paragraph further discusses how the solutions to differential equations can provide families of functions rather than a single function, with the example of a ball's position being determined by an equation involving both time and constants representing initial conditions. The influence of air resistance on the falling object is also mentioned, indicating the need for more complex differential equations to model real-world scenarios accurately.
🌳 Malthus's Model and the Reality of Population Growth
The paragraph introduces Malthus's model of population growth, which posits that the change in population is proportional to the population size itself, leading to exponential growth. It critiques the model as being unrealistic over long periods due to the impossibility of infinite growth. To analyze the solution to the differential equation representing this model without finding an explicit formula, the paragraph introduces the concept of a direction field, which visualizes the slope of the tangent line (the derivative) at various points in the time-population plane. This method allows for the sketching of the solution's trajectory given an initial condition.
🌿 Refining Population Growth Models with Carrying Capacity
Building upon Malthus's model, this section introduces refinements that account for environmental limitations, such as the carrying capacity. The paragraph presents the fair host model, or logistic equation, which includes a carrying capacity (k) and adjusts the growth rate based on the population's proximity to this limit. The direction field method is again used to visualize the behavior of the population over time, illustrating how populations starting below the carrying capacity will rise towards it, while those above will decline. The paragraph also touches on the concept of a threshold population below which the population will not grow but will instead shrink.
🕊️ The Role of Differential Equations in Describing Real-World Phenomena
This final paragraph highlights the diverse contexts in which differential equations are applied, such as the spread of epidemics, hormone balance, chemical reactions, and planetary motion. It also mentions an upcoming lecture on predator-prey dynamics and stringed instruments, emphasizing the versatility and importance of differential equations in modeling a wide range of real-world phenomena.
Mindmap
Keywords
💡Mathematical Model
💡Derivative
💡Differential Equation
💡Continuous Compounding
💡Initial Condition
💡Newton's Second Law
💡Direction Field
💡Carrying Capacity
💡Malthusian Model
💡Logistic Equation
Highlights
Mathematics and calculus are powerful tools for understanding and manipulating the world through mathematical models.
A mathematical model can predict features of the world, exemplified by calculating the growth of money in a savings account with continuous compounding.
The concept of interest rates in savings accounts is related to the derivative, which captures the rate of change of a function.
Differential equations are used to model the rate of change and can be applied to various scientific and social science fields.
Newton and Leibniz were pioneers in writing down differential equations, marking the beginning of calculus.
Differential equations are central to describing issues in physics, biology, economics, and social sciences.
The rate at which an object falls can be described using a differential equation relating its velocity to time.
The solution to a differential equation is a function, not a number, and can represent a family of functions.
Initial conditions are crucial for narrowing down a specific solution from a family of functions in differential equations.
Differential equations can account for real-world factors like air resistance in the motion of falling objects.
Newton's second law of physics, relating force, mass, and acceleration, often results in differential equations.
The Bernoulli family significantly contributed to the development of calculus and differential equations in the 17th and 18th centuries.
Joseph Louis Lagrange and Pierre Simon de Laplace made significant contributions to solving differential equations.
Direction fields are a method for analyzing the solution of a differential equation without finding an explicit formula.
Malthus's model of population growth is a simple exponential model that is unrealistic for long-term predictions.
The carrying capacity concept introduces an upper limit to population growth, making models more realistic.
The logistic equation, or Verhulst model, incorporates carrying capacity to create a more accurate population growth model.
Direction fields can be used to visualize the behavior of solutions to differential equations in population models.
Combining threshold and carrying capacity in population models can lead to more accurate predictions, as seen in the case of the passenger pigeon.
Differential equations have wide-ranging applications, including in the study of epidemics, hormone balance, chemical reactions, and planetary motion.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: