Uniform Circular Motion, Example #2 stone whirled in circle
TLDRIn this educational video, the presenter tackles a physics problem involving a stone in uniform circular motion that breaks free, exhibiting projectile motion. The initial question posed is the direction the stone will travel once the string snaps, with the correct answer being a straight line due to inertia. The problem then shifts to calculating centripetal acceleration, which requires determining the stone's speed first. By analyzing the projectile motion—10 meters horizontally and a 2-meter drop—the presenter uses kinematics to find the time of flight and horizontal velocity. Finally, centripetal acceleration is calculated using the speed and the circle's radius, resulting in 163 meters per second squared, effectively blending concepts of circular and projectile motion.
Takeaways
- 😀 The example is more challenging and involves multiple topics.
- 💡 A boy is rotating a stone in a horizontal circle, and the stone breaks, leading to projectile motion.
- 🧐 The first question is about the direction the stone will go when the string snaps.
- 🌀 Many people think the stone will continue in a circle or go straight out due to an outward force.
- 📏 The correct answer is the stone will go in a straight line due to inertia.
- 🔄 Objects in motion will continue in the same straight-line motion when no force acts on them.
- 📐 The problem involves finding the centripetal acceleration with given parameters.
- 📝 The given parameters include the radius of 1.5 meters, horizontal distance of 10 meters, and vertical height of 2 meters.
- 🔍 The challenge is to find the velocity, which is needed to calculate the centripetal acceleration.
- 🚀 The problem combines projectile motion and uniform circular motion concepts.
- 🕰️ Time in the air is calculated using kinematic equations to find horizontal velocity.
- ⚙️ The final centripetal acceleration is calculated using the formula \( a_c = \frac{V^2}{R} \).
Q & A
What is the main challenge in example number two?
-The main challenge in example number two is that it involves multiple topics and includes an additional complexity of mixing projectile motion with uniform circular motion.
What happens when the stone breaks off from the string in the circular motion?
-When the stone breaks off from the string, it will move in a straight line tangent to the point of breakage due to inertia, as objects in motion continue in a straight line unless acted upon by an external force.
Why is the direction of the stone's movement straight after the string snaps?
-The direction of the stone's movement is straight because of inertia, which states that an object in motion will continue in a straight line at constant velocity unless acted upon by an external force.
What is centripetal acceleration and how is it calculated?
-Centripetal acceleration is the acceleration that keeps an object moving in a circular path. It is calculated using the formula a_c = V^2 / R, where V is the velocity and R is the radius of the circle.
Why can't the speed of the stone be calculated using the formula 2πR/T?
-The speed of the stone cannot be calculated using the formula 2πR/T because the period (T) or the number of cycles per minute is not provided in the problem.
How is the horizontal velocity of the stone determined?
-The horizontal velocity of the stone is determined by analyzing the projectile motion after the string breaks. Using the known horizontal distance traveled (10 meters) and the time in the air (0.639 seconds), the horizontal velocity is calculated.
What information is needed to find the time the stone is in the air?
-To find the time the stone is in the air, the initial vertical height (2 meters), the vertical acceleration (9.8 m/s^2), and the fact that the initial vertical velocity is zero are needed.
How is the time of flight for the projectile motion calculated?
-The time of flight is calculated using the kinematic equation y = y0 + v0y * t + 0.5 * a * t^2, where the final vertical position is zero, the initial vertical height is 2 meters, and the vertical acceleration is -9.8 m/s^2.
What is the calculated horizontal velocity of the stone after the string breaks?
-The calculated horizontal velocity of the stone after the string breaks is approximately 15.65 meters per second.
What is the final centripetal acceleration of the stone before the string snaps?
-The final centripetal acceleration of the stone before the string snaps is calculated to be 163 meters per second squared, using the horizontal velocity (15.65 m/s) and the radius (1.5 meters).
Outlines
🔁 Circular Motion and Projectile Path
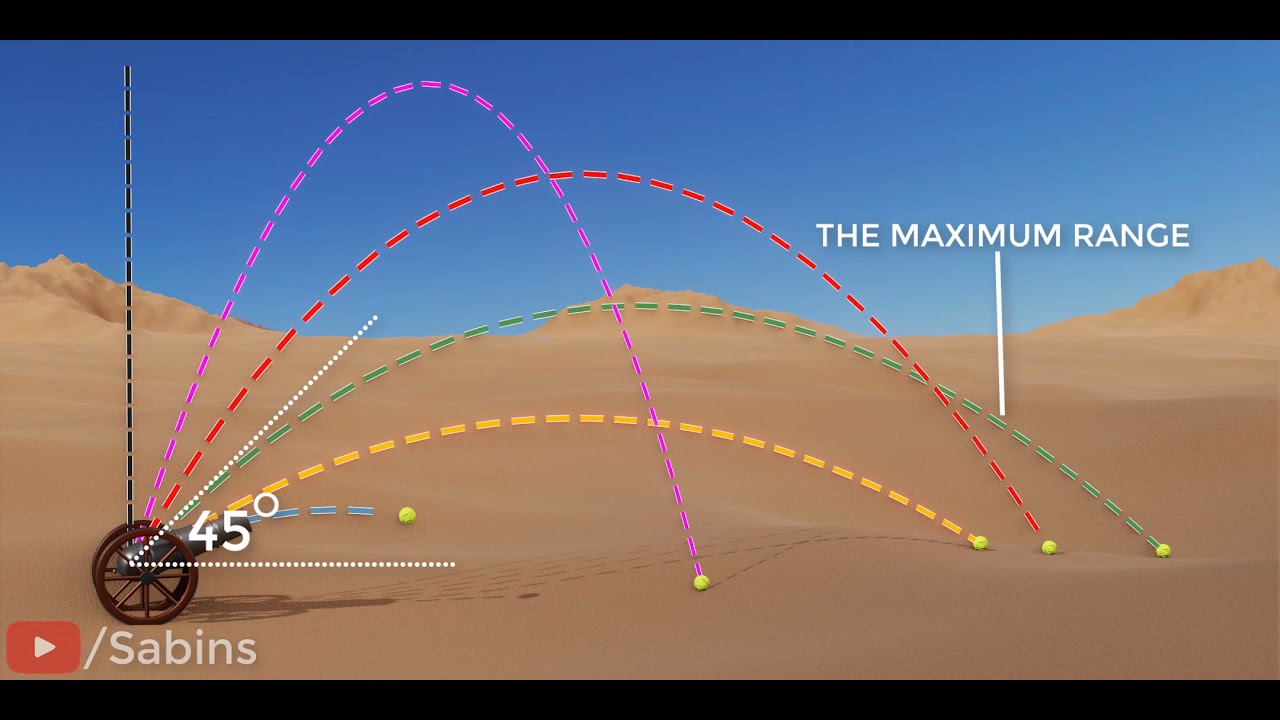
This paragraph introduces a physics problem involving a boy swinging a stone in a horizontal circle, which then breaks free and follows a projectile motion path. The main question posed is the direction the stone will take after the string snaps. The instructor explains that due to inertia, the stone will continue in a straight line, which is option B. The problem then shifts to calculating the centripetal acceleration, with given information about the circle's radius and the horizontal and vertical distances involved. The challenge is that the speed of the stone is not directly known, requiring an alternative approach to find it.
📚 Solving for Centripetal Acceleration
The second paragraph delves into the calculations necessary to find the centripetal acceleration of the stone in its circular motion. The instructor acknowledges the lack of direct information about the period of the motion or the speed of the stone, necessitating a different method to find the velocity. By visualizing the motion as a projectile problem with given vertical and horizontal distances, the instructor uses kinematic equations to first determine the time the stone spends in the air, which is approximately 0.639 seconds. With this time, the horizontal velocity of the stone at the moment of release is calculated to be 15.65 meters per second. Finally, this velocity is used in the centripetal acceleration formula, yielding an acceleration of 163 meters per second squared.
Mindmap
Keywords
💡Uniform Circular Motion
💡Centripetal Acceleration
💡Inertia
💡Projectile Motion
💡Kinematics
💡Velocity
💡Acceleration
💡Radius
💡Horizontal Distance
💡Vertical Height
Highlights
Introduction to a more challenging physics problem involving a stone in circular motion and projectile motion.
The stone is initially in a horizontal circular motion before breaking and following a projectile path.
The direction of the stone's motion after the string snaps is a key question posed to the audience.
Explanation of common misconceptions regarding the stone's trajectory after the string breaks.
Introduction to the concept of inertia as it relates to the stone's motion.
Inertia causes the stone to continue in a straight line after the string breaks.
The need to calculate centripetal acceleration with given information about the circle's radius and distances.
Challenge of finding the stone's speed without knowing the period of the circular motion.
The problem is a combination of projectile motion and uniform circular motion.
Setting up a coordinate system to analyze the projectile motion.
Using kinematic equations to find the time the stone is in the air.
Calculation of the stone's horizontal velocity based on its horizontal displacement and time.
Determination of the centripetal acceleration using the horizontal velocity and the circle's radius.
Final calculation of the centripetal acceleration resulting in 163 meters per second squared.
The importance of understanding inertia and its effects on motion in physics problems.
The practical application of physics concepts in analyzing real-world scenarios like the stone's motion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: