Where Does The Range Equation Come From?
TLDRThe video script delves into the physics of projectile motion, focusing on the Range Equation. It explains how to calculate the horizontal distance, or range, a projectile will travel when fired at an angle above the horizontal axis. The key concept is separating the motion into horizontal (x-axis) and vertical (y-axis) components, with the horizontal component being solely determined by the initial speed and angle, and the vertical component being influenced by gravity. The video simplifies the mathematical process by using kinematic variables and double angle identities to derive the Range Equation, which is expressed as the square of the initial speed times the sine of double the angle, divided by the acceleration due to gravity (g).
Takeaways
- 🎯 The Range Equation is used to determine the horizontal distance a projectile will travel.
- 🚀 A projectile is launched with an initial speed (s) at an angle (theta) above the horizontal axis.
- 📈 The projectile's motion is influenced by gravity, accelerating downward at a rate of g (9.81 m/s^2 on Earth).
- 🔄 The motion is separated into horizontal (x-axis) and vertical (y-axis) components for analysis.
- 🌐 The horizontal displacement (range r) is the primary focus of the Range Equation.
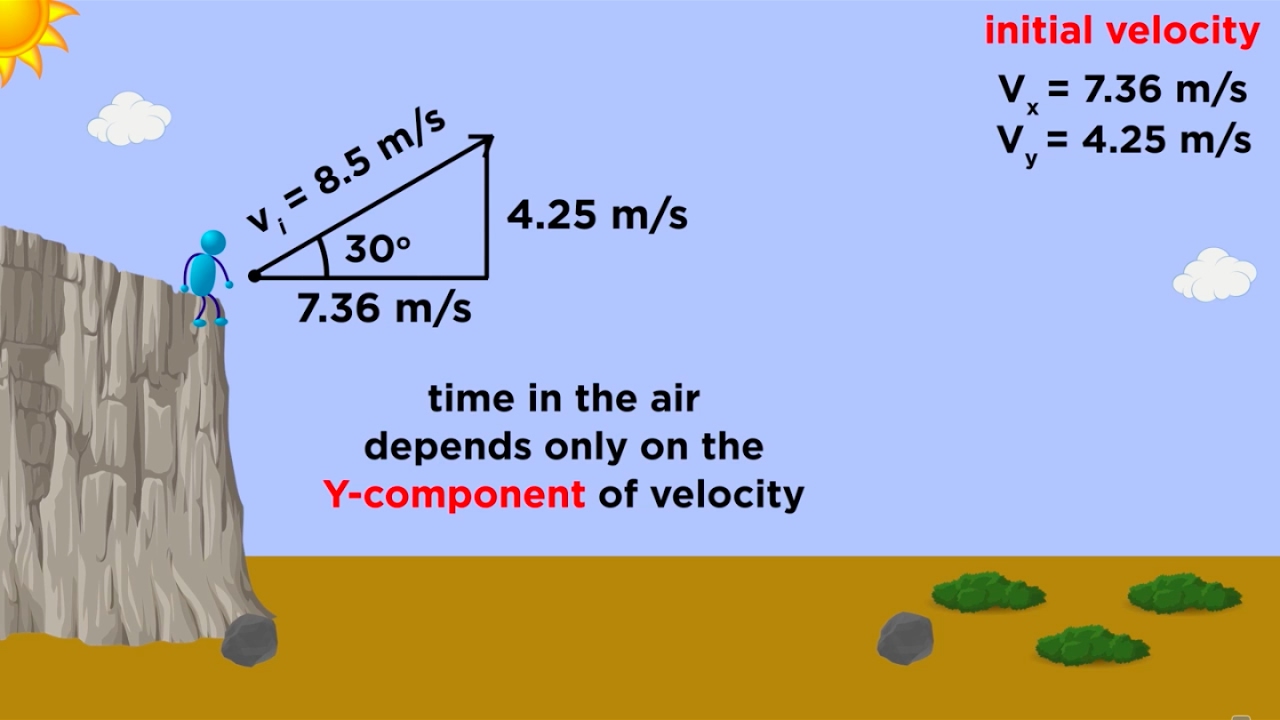
- 📐 The horizontal component of the initial velocity is calculated as s*cosine(theta).
- 🔽 On the y-axis, there is no horizontal acceleration, making it zero, while the vertical acceleration is -g (negative due to downward direction).
- 🕒 The time of flight is the same for both axes, allowing the equations to be set equal to each other.
- 🔢 The Range Equation is derived by applying kinematic displacement formulas to both axes and solving for time.
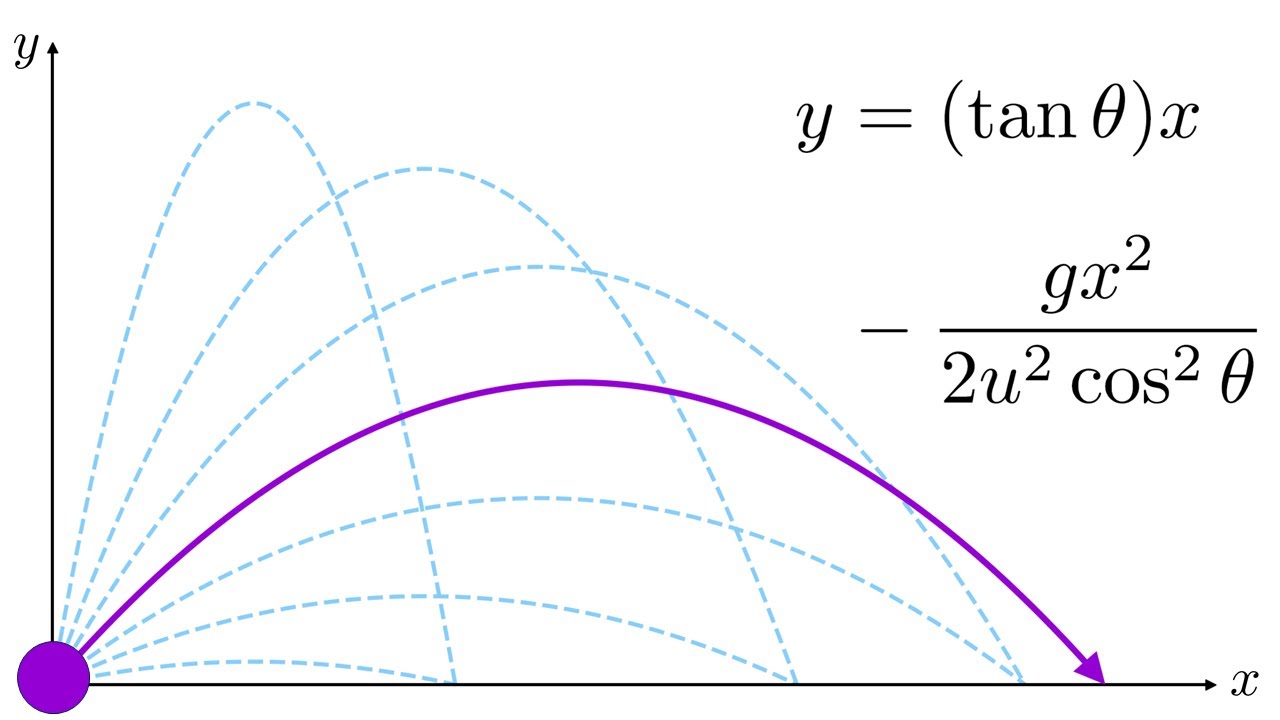
- 🌟 The final form of the Range Equation is s^2 * sin(2*theta) / g, using the double angle identity sin(2*theta) = 2*sin(theta)*cos(theta).
- 📋 This equation helps in understanding and predicting the trajectory and range of projectiles in physics and engineering applications.
Q & A
What is the range equation in projectile motion?
-The range equation is used to determine the horizontal distance (range) that a projectile will travel when launched at a certain initial speed and angle above the horizontal axis, considering the acceleration due to gravity.
Why is it necessary to separate the motion of a projectile into the x-axis and y-axis?
-Separating the motion into the x and y axes allows us to analyze the horizontal and vertical components of the projectile's motion independently, simplifying the complex two-dimensional motion into two one-dimensional motions.
What is the horizontal displacement in the context of the range equation?
-The horizontal displacement, denoted as 'r', is the range we are trying to solve for in the range equation. It represents the total horizontal distance the projectile travels before landing at the same height from which it was fired.
How is the initial speed broken up in the context of projectile motion?
-The initial speed is broken up into its horizontal and vertical components. The horizontal component is given by the initial speed multiplied by the cosine of the launch angle (s*cosine(theta)), and the vertical component by the initial speed multiplied by the sine of the launch angle (s*sine(theta)).
What is the acceleration of a projectile in the horizontal direction?
-In the horizontal direction, a projectile experiences zero acceleration because there is no force acting horizontally (assuming air resistance is negligible). Thus, the horizontal velocity remains constant throughout the motion.
What is the acceleration in the vertical direction for a projectile?
-The acceleration in the vertical direction is due to gravity, which is approximately 9.81 meters per second squared (m/s^2) on Earth. Since gravity acts downward, it is considered a negative value in the equations (-g).
How is the range equation derived?
-The range equation is derived by applying the kinematic displacement formulas to both the x-axis (horizontal) and y-axis (vertical), and then setting the times for both axes equal to each other since the projectile is in the air for the same amount of time in both directions. After rearranging and simplifying, the equation involves the initial speed, the launch angle, and the acceleration due to gravity.
What is the significance of the sine of two theta (sin(2theta)) in the range equation?
-The sine of two theta (sin(2theta)) is a result of using double angle identities in the range equation. It represents the combined effect of the launch angle on both the horizontal and vertical components of the projectile's motion and is crucial for calculating the maximum range.
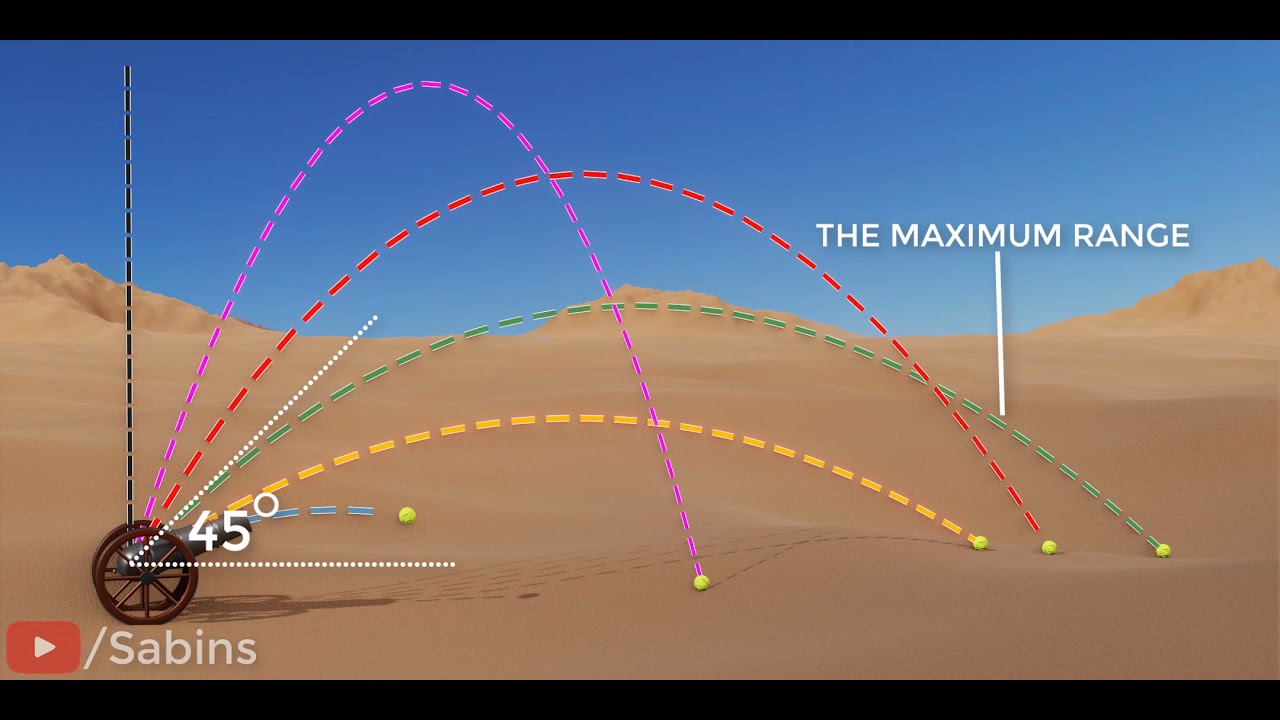
At what launch angle does a projectile have the maximum range?
-A projectile has the maximum range when launched at a launch angle of 45 degrees, assuming no air resistance. This is because sin(2*45°) = sin(90°) = 1, which maximizes the value of the sine function in the range equation.
How does the shape of the sin(theta) graph relate to the range of a projectile?
-The shape of the sin(theta) graph shows that the range increases as the launch angle approaches 45 degrees. When theta is 45 degrees, sin(theta) reaches its maximum value, and thus the range is maximized. The graph also shows that complementary angles (angles adding up to 90 degrees) result in the same range.
What happens to the range of a projectile if air resistance is considered?
-If air resistance is considered, the actual range of a projectile will be less than predicted by the range equation, which assumes no air resistance. The presence of air resistance affects the motion of the projectile, particularly the horizontal and vertical components of its velocity, leading to a shorter range.
How does the range equation apply to real-world scenarios?
-The range equation is applicable in various real-world scenarios, such as sports (e.g., archery, baseball), military operations (e.g., firing炮弹), and engineering (e.g., designing catapults or calculating trajectories for space launches). It provides a fundamental understanding of how projectiles move under the influence of gravity and can be used to optimize the launch conditions for achieving desired ranges.
Outlines
🎯 Understanding the Range Equation
This paragraph introduces the concept of the range equation in the context of projectile motion. It explains the process of firing a projectile at an initial speed and angle, and the goal of determining the horizontal distance (range) it travels before landing at the same height from which it was fired. The paragraph delves into the physics of projectile motion, highlighting the influence of gravity and the separation of motion into horizontal (x-axis) and vertical (y-axis) components. It emphasizes the importance of analyzing the initial velocity's horizontal and vertical components and understanding the acceleration due to gravity (g). The paragraph concludes with the derivation of the range equation, which is a fundamental formula for calculating the distance a projectile will travel horizontally.
Mindmap
Keywords
💡Projectile Motion
💡Range Equation
💡Initial Speed (s)
💡Angle of Projection (theta)
💡Acceleration due to Gravity (g)
💡Horizontal Displacement (r)
💡Kinematic Equations
💡Horizontal Component
💡Vertical Component
💡Displacement Formula
💡Double Angle Identity
Highlights
The concept of the range equation is introduced, which is used to determine the horizontal distance a projectile will travel.
The initial speed of the projectile is denoted by 's' and the angle above the horizontal axis is denoted by 'theta'.
The projectile is assumed to accelerate downward under the influence of gravity at a rate of 'g', which is 9.81 meters per second squared on Earth.
The motion of the projectile is separated into the x-axis and the y-axis for analysis.
The horizontal displacement 'r' is the range that the equation aims to solve for.
The initial velocity is broken up into its horizontal and vertical components, with the horizontal component being 's cosine theta'.
On the x-axis, the horizontal acceleration is zero, meaning the final velocity is the same as the initial.
The vertical displacement on the y-axis is zero, and the initial vertical velocity is 's sine theta'.
The acceleration on the y-axis is negative 'g' due to the downward direction of gravity.
The displacement formula from the kinematic equations is applied to both the x-axis and y-axis to derive the range equation.
The times for both axes are set equal to each other since the projectile is in the air for the same amount of time horizontally and vertically.
Algebra is used to rearrange and solve for 'r', resulting in the range equation.
The final form of the range equation is derived as 's squared over g, times the sine of two theta'.
The use of double angle identities simplifies the range equation to a more recognizable form.
The range equation provides a practical application for predicting the trajectory of projectiles in physics and engineering.
This method can be applied to various projectile scenarios, from archers firing arrows to modern battle tanks firing shells.
Understanding the range equation is crucial for fields that involve the calculation of projectile motion and its applications.
The step-by-step derivation of the range equation demonstrates the power of combining mathematical principles with real-world physics problems.
The range equation is a fundamental concept in kinematics and has a wide range of applications beyond just projectile motion.
The explanation provided in the transcript is a clear and detailed breakdown of the range equation, making it accessible to learners at various levels.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: