Vector components from magnitude and direction
TLDRThis video script offers a clear and engaging explanation on how to break down a vector into its horizontal (x) and vertical (y) components using trigonometry. The process involves understanding the magnitude and direction of a vector, represented by an angle with the positive x-axis. By constructing a right triangle and applying the Soh-Cah-Toa mnemonic for trigonometric functions, the script demonstrates how to find the x component using cosine and the y component using sine, both multiplied by the vector's magnitude. The video also addresses the impact of the vector's quadrant on the signs of these components. The explanation further clarifies the concept using the unit circle definition of trigonometric functions, showing how cosine relates to the x-coordinate and sine to the y-coordinate on the unit circle. The script is practical, providing a step-by-step guide complete with approximate calculator evaluations, making it accessible for viewers to understand the mathematical principles behind vector resolution.
Takeaways
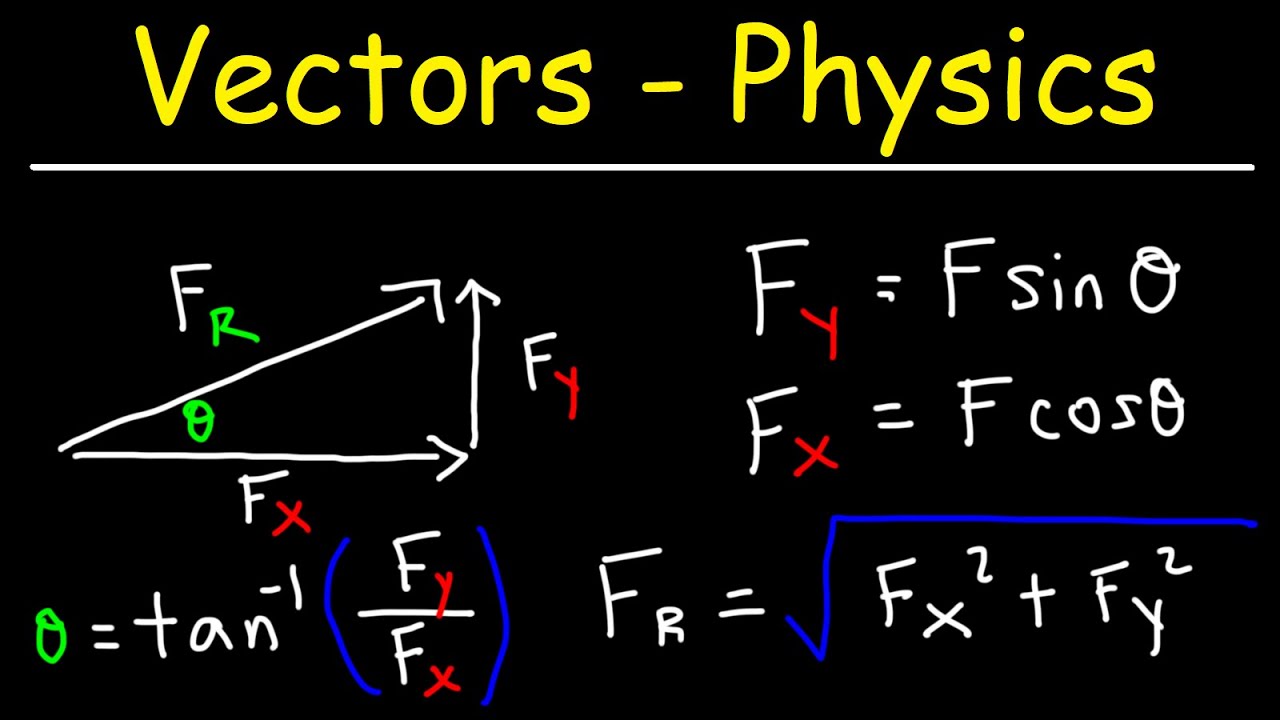
- 📐 To find the x and y components of a vector given its magnitude and angle with the positive x-axis, you can use trigonometry.
- 📈 The horizontal (x) component of a vector is found by multiplying the cosine of the given angle by the vector's magnitude.
- 📉 The vertical (y) component of a vector is found by multiplying the sine of the given angle by the vector's magnitude.
- 🔄 In a right triangle, the cosine function relates the adjacent side to the hypotenuse, while the sine function relates the opposite side to the hypotenuse.
- 🧮 If no calculator is available, you can express the components in terms of the cosine and sine of the angle multiplied by the magnitude.
- 📉 For vectors in the second quadrant, the x component is negative, and the y component is positive.
- 🤔 The unit circle definition of trigonometric functions helps in understanding that the cosine of an angle is the x-coordinate and the sine is the y-coordinate on the circle.
- 🌀 If the vector magnitude is not one (a unit vector), you multiply the cosine and sine by the magnitude to get the components.
- 📊 The process can be visualized by drawing a right triangle where the vector lies, making it easier to apply the Soh-Cah-Toa mnemonic for trigonometric ratios.
- 🔢 Using a calculator, you can approximate the x and y components by finding the cosine and sine of the given angle and then multiplying by the magnitude.
- 📌 The direction of the vector component (positive or negative) depends on the quadrant in which the terminal point of the vector lies.
Q & A
What is the main concept being discussed in the transcript?
-The main concept discussed in the transcript is the conversion of a vector's magnitude and direction, given as an angle with the positive x-axis, into its x and y components using trigonometry.
What is the Soh-Cah-Toa definition mentioned in the transcript?
-Soh-Cah-Toa is a mnemonic used to remember the basic trigonometric functions: Sine (sin) is Opposite over Hypotenuse, Cosine (cos) is Adjacent over Hypotenuse, and Tangent (tan) is Opposite over Adjacent.
How does the cosine function relate to the x-component of a vector?
-The cosine function relates to the x-component of a vector by giving the ratio of the length of the adjacent side (x-component) to the length of the hypotenuse (vector's magnitude) in a right-angled triangle formed by the vector.
How does the sine function relate to the y-component of a vector?
-The sine function relates to the y-component of a vector by giving the ratio of the length of the opposite side (y-component) to the length of the hypotenuse (vector's magnitude) in a right-angled triangle formed by the vector.
What happens to the x and y components of a vector when it is in the second quadrant?
-When a vector is in the second quadrant, the x-component becomes negative while the y-component remains positive, due to the properties of the coordinate system and the direction of the vector.
How is the magnitude of a vector factored into the calculation of its components?
-The magnitude of a vector is factored into the calculation of its components by multiplying the cosine of the angle by the magnitude for the x-component, and the sine of the angle by the magnitude for the y-component.
What is the unit circle definition of trigonometric functions?
-The unit circle definition of trigonometric functions states that for a point on the unit circle (a circle with radius one), the cosine is the x-coordinate of that point, and the sine is the y-coordinate of that point.
How does the magnitude of a vector affect its components?
-The magnitude of a vector affects its components by scaling them up or down. If the vector has a magnitude of four, for example, both the x and y components will be four times larger than if it were a unit vector.
What is the approximate value of the x-component of a vector with a magnitude of four and an angle of 50 degrees?
-The approximate value of the x-component is 2.57, which is obtained by multiplying the cosine of 50 degrees by the magnitude, which is four.
What is the approximate value of the y-component of a vector with a magnitude of four and an angle of 50 degrees?
-The approximate value of the y-component is 3.06, which is obtained by multiplying the sine of 50 degrees by the magnitude, which is four.
How does the process of finding vector components change when the vector is in a different quadrant, such as the second quadrant?
-In the second quadrant, the x-component of the vector becomes negative while the y-component remains positive. The process involves using the cosine of the angle for the x-component and the sine of the angle for the y-component, then considering the sign based on the quadrant.
What is the significance of the supplementary angle in the context of the second quadrant vector?
-The supplementary angle is used to find the adjacent side of the right triangle formed by the vector components when the terminal point of the vector is in the second quadrant. It helps in determining the correct sign for the x-component, which is negative in this case.
Outlines
📐 Vector Magnitude and Direction to Components
This paragraph explains the process of converting a vector's magnitude and direction, given by an angle with the positive x-axis, into its x and y components. It involves basic trigonometry and the use of the Soh-Cah-Toa mnemonic for the trigonometric functions. The explanation includes drawing a right triangle to represent the vector's components and applying the cosine for the adjacent side over the hypotenuse and sine for the opposite side over the hypotenuse to find the x and y components. The vector is then approximated using a calculator, with the x component calculated as approximately 2.57 and the y component as approximately 3.06, after multiplying the cosine and sine of 50 degrees by the vector's magnitude, which is four in this case.
🧭 Vector Components in the Second Quadrant
The second paragraph discusses finding the x and y components of a vector whose terminal point lies in the second quadrant. This means the x component will be negative, and the y component will be positive. The process is similar to the first paragraph, using the cosine of 135 degrees for the x component and the sine of 135 degrees for the y component, both multiplied by the vector's magnitude, which is ten in this scenario. The calculations result in an x component of approximately -7.07 and a y component of approximately 7.07. The paragraph also touches on the unit circle concept, explaining that for a unit vector at 135 degrees, the coordinates would be the cosine and sine of that angle, and since the given vector has ten times the magnitude, its components will also be ten times larger.
🔢 Calculating Vector Components with a Calculator
The final paragraph briefly mentions the use of a calculator to find the precise values of the vector components that were approximated in the previous paragraphs. It implies that the actual calculations would yield more accurate results for the x and y components of the vectors discussed, which were found to be approximately 2.57 and 3.06 for the first vector, and -7.07 and 7.07 for the second vector, respectively.
Mindmap
Keywords
💡Vector
💡Magnitude
💡Direction
💡X and Y Components
💡Trigonometry
💡Soh-Cah-Toa
💡Cosine
💡Sine
💡Unit Circle
💡Right Triangle
💡Second Quadrant
Highlights
The process involves converting a vector's magnitude and direction into its x and y components using trigonometry.
A right triangle is constructed to apply basic trigonometric definitions from the Soh-Cah-Toa mnemonic.
The cosine function is used to find the adjacent side (x component) over the hypotenuse (vector's magnitude).
The sine function is applied to determine the opposite side (y component) relative to the hypotenuse.
The x component of a vector is found by multiplying the cosine of the given angle by the vector's magnitude.
Similarly, the y component is calculated by multiplying the sine of the angle by the vector's magnitude.
The unit circle definition of trigonometric functions is introduced as an alternative method for finding vector components.
The x coordinate of a unit circle intersection represents the cosine of the angle, and the y coordinate represents the sine.
For a vector with a magnitude other than one, the components are scaled by the vector's magnitude.
A calculator is used to approximate the values of the trigonometric functions for specific angles.
The x component of a vector in the second quadrant is negative, and the y component is positive.
The process is demonstrated for a vector with a 135-degree angle, resulting in a negative x component and a positive y component.
The supplementary angle is used to find the magnitude of the vector's components in the second quadrant.
The concept of direction is crucial when determining the sign (positive or negative) of the vector components.
The video concludes by reinforcing the method's applicability and the importance of understanding vector direction for accurate calculations.
Practical applications of vector component calculations are implied for fields involving vector mathematics, such as physics and engineering.
The importance of a clear understanding of trigonometric functions and their application to vector analysis is emphasized.
Transcripts
Browse More Related Video
Vectors - Basic Introduction - Physics

Trig 0.2 - Trig Functions Defined on the Unit Circle

17 - Calculating Vector Components in Physics, Part 1 (Component form of a Vector)
AP Physics B Kinematics Presentation #69

How To Find The Components of a Vector Given Magnitude and Direction
05 - Sine and Cosine - Definition & Meaning - Part 1 - What is Sin(x) & Cos(x) ?
5.0 / 5 (0 votes)
Thanks for rating: