How to Convert From Polar Equations to Rectangular Equations (Precalculus - Trigonometry 40)
TLDRThe video script is an educational guide on converting polar equations to rectangular form. It begins by explaining the basic conversion process, where 'r squared' is replaced with 'x squared plus y squared', and 'r cosine theta' or 'r sine theta' is replaced with 'x' or 'y', respectively. The script then delves into more complex scenarios, such as multiplying both sides of an equation by 'r' to facilitate conversion, and handling cases where the equation does not readily provide the needed 'r squared' or trigonometric terms. The guide also emphasizes the importance of avoiding unnecessary complications, such as multiplying by 'r' when it could complicate the equation. It illustrates the process with several examples, including converting the equation 'r equals sine theta plus one' and 'r equals 3 cosecant theta', and concludes with a discussion on converting simple equations like 'r equals 2', which represents a circle with a radius of two. The script is designed to help users become comfortable with both polar and rectangular coordinate systems and to understand the conditions under which each might be preferable for solving a given problem.
Takeaways
- 📐 **Polar to Rectangular Conversion**: Replace r² with x² + y², r*cos(θ) with x, and r*sin(θ) with y to convert polar equations to rectangular form.
- 🔄 **Reverse Process**: The conversion from polar to rectangular coordinates is the reverse of the process taught in the previous video, using the relationships between r, θ, x, and y.
- ⚙️ **Multiplication by r**: Multiplying both sides of a polar equation by r can simplify the equation, especially when terms like r*cos(θ) or r*sin(θ) are present.
- 🔢 **Dealing with r²**: When an equation lacks an r² term, multiplying by r can introduce it, which is helpful for converting to rectangular form.
- 🔁 **Squaring Both Sides**: Squaring both sides of an equation can eliminate fractions and simplify the conversion process.
- 🚫 **Avoiding Explosion**: Be cautious not to multiply by r when it will complicate the equation by creating excessive r terms or losing valuable x or y terms.
- 🔍 **Looking for Identities**: Identifying trigonometric identities within the equation can simplify the conversion process.
- 📉 **Eliminating Fractions**: Getting rid of fractions by multiplying by denominators is often a helpful step before multiplying by r.
- 🔄 **Reciprocal Functions**: Change reciprocal functions like secant and cosecant to their trigonometric equivalents to simplify the equation.
- 🧮 **Solving for r**: If stuck with an r term, solve for r using the relationship r = sqrt(x² + y²) and then replace it in the equation.
- ⭕️ **Circle Equation**: The equation r = constant represents a circle with that constant as its radius, which can be directly converted to x² + y² = constant² in rectangular form.
Q & A
What is the basic process of converting polar equations to rectangular form?
-The basic process involves replacing every instance of r^2 with x^2 + y^2, r * cos(θ) with x, and r * sin(θ) with y. If the equation does not have these forms, you may need to multiply both sides by r to introduce them.
Why is it helpful to multiply both sides of a polar equation by r?
-Multiplying both sides by r is helpful because it can introduce r^2, r * cos(θ), or r * sin(θ) into the equation, which makes it easier to convert to rectangular form using the substitutions x^2 + y^2 for r^2, x for r * cos(θ), and y for r * sin(θ).
What is the first step to take when converting the polar equation r = cos(θ)?
-The first step is to multiply both sides by r to get r^2 = r * cos(θ), which then allows you to use the substitutions to convert to rectangular form.
How can you deal with an equation like r = sin(θ) + 1, which does not have an obvious r^2, r * sin(θ), or r * cos(θ)?
-You can multiply both sides by r to distribute it across the equation, which will introduce r^2 and r * sin(θ) terms that can be converted using the standard substitutions.
What is the purpose of using the Pythagorean theorem in converting polar to rectangular equations?
-The Pythagorean theorem (x^2 + y^2 = r^2) is used to replace r^2 with x^2 + y^2 in the polar equation, which is a crucial step in converting the equation into rectangular form.
How do you handle a polar equation with a reciprocal function like r = 3 csc(θ)?
-First, you convert the reciprocal function to its trigonometric equivalent (csc(θ) becomes 1/sin(θ)), then multiply both sides by sin(θ) to eliminate the fraction, which results in r * sin(θ) = 3, and then replace r * sin(θ) with y to find the rectangular form.
What is the strategy when you encounter a polar equation that seems complex and does not have clear r^2 or trigonometric terms?
-You can try to multiply both sides by r or a combination of r's to create x and y terms from the trigonometric functions. This may involve recognizing identities or using algebraic manipulation to simplify the equation.
Why might multiplying both sides of an equation by r not always be the best approach?
-Multiplying by r can sometimes complicate the equation by introducing additional r terms that are difficult to handle, especially if they end up in denominators or create more complex expressions that are harder to simplify.
How does the process of converting polar equations to rectangular form help in graphing these equations?
-Converting to rectangular form can make it easier to graph the equations, especially if you are more familiar with Cartesian coordinates. It can also reveal the shapes of the graphs more clearly, such as identifying a circle or a parabola.
What is the final form of the rectangular equation obtained from the polar equation r = 2?
-The final form of the rectangular equation is x^2 + y^2 = 4, which represents a circle with a radius of 2 centered at the origin.
How can you identify and utilize trigonometric identities when converting polar equations to rectangular form?
-You can recognize identities like sin(θ)/cos(θ) being equivalent to tan(θ), which can be converted to y/x. Utilizing these identities can simplify the conversion process and help in transforming the polar equation into a more recognizable rectangular form.
Outlines
📐 Introduction to Polar to Rectangular Conversion
This paragraph introduces the concept of converting polar equations to rectangular form. It emphasizes the utility of this conversion for gaining a better understanding of the图形 (geometry) and for situations where rectangular equations may be more straightforward to work with. The process involves substituting r² for x² + y², x for r*cos(θ), and y for r*sin(θ), and also highlights the technique of multiplying both sides of a polar equation by r to facilitate the conversion.
🔢 Dealing with r and Trigonometric Functions
The second paragraph delves into how to handle the variable r in polar equations when it does not appear in the form of r² or with a trigonometric function. It explains that multiplying both sides of the equation by r can help, allowing the conversion of terms like r*cos(θ) to x and r*sin(θ) to y. The paragraph also addresses the conversion of more complex equations, such as those involving r equals sine theta plus one, by multiplying by r and applying the Pythagorean theorem and trigonometric identities.
🤔 Strategies for Complex Polar Equations
The third paragraph discusses strategies for dealing with complex polar equations that do not immediately lend themselves to conversion. It suggests looking for trigonometric identities and using algebraic manipulations to eliminate fractions. The paragraph also covers the conversion of equations involving reciprocal trigonometric functions, such as cosecant and secant, and how to treat them by converting them into their respective trigonometric functions before proceeding with the conversion.
🧮 Multiplying by r and Factoring
This paragraph focuses on the algebraic technique of multiplying an equation by r or by powers of r to create the necessary components for conversion to rectangular form. It explains how to deal with missing parts in an equation by multiplying by additional r's to generate x and y terms. The paragraph also illustrates the conversion process with an example equation, r equals sine theta cosine squared theta, and shows alternative methods to achieve the conversion.
🔁 Conversion Examples and Insights
The fifth paragraph provides examples of converting polar equations to rectangular form, emphasizing the thought process and decision-making behind each step. It discusses the conversion of simple equations like r equals 2, which results in a circle with a radius of two, and more complex ones, like r minus r*cos(θ) equals 4. The paragraph also warns against choices that may complicate the equation and suggests verifying steps if the process seems to be leading to a more complicated result.
📚 Final Thoughts on Polar to Rectangular Conversion
The final paragraph summarizes the process of converting polar equations to rectangular form. It reiterates the importance of understanding both coordinate systems and knowing when one might be preferred over the other. The paragraph encourages practice and provides assurance that with the right approach and understanding of the underlying principles, one can successfully convert between polar and rectangular equations.
Mindmap
Keywords
💡Polar Equations
💡Rectangular Coordinates
💡Conversion
💡r-Squared (r^2)
💡r Cosine Theta (r cos θ)
💡r Sine Theta (r sin θ)
💡Multiplying by r
💡Squaring Both Sides
💡Trigonometric Identities
💡Reciprocal Trigonometric Functions
💡Graphing
Highlights
Conversion from polar to rectangular coordinates involves replacing r^2 with x^2 + y^2, r*cos(θ) with x, and r*sin(θ) with y.
Multiplying both sides of a polar equation by r can be helpful, especially when dealing with terms like r*cos(θ) or r*sin(θ).
When an equation lacks r^2 or r terms, multiplying by r can introduce them, aiding in conversion to rectangular form.
The process of converting polar to rectangular can simplify equations, making them easier to work with in certain contexts.
r = cos(θ) can be multiplied by r to yield r^2 = x^2 + y^2, which is useful for conversion.
The equation r = sin(θ) + 1 demonstrates the process of multiplying by r to facilitate conversion.
Dealing with plus r terms after multiplying by r requires careful consideration to avoid unnecessary complications.
When all r terms are used up and only x and y remain, the equation can often be simplified or solved.
r^2 = cos(θ) can be approached by multiplying by r to get r^2 * r = x, leveraging trigonometric identities.
Alternative methods for conversion exist, such as dealing with the denominator directly in certain cases.
Eliminating fractions by multiplying by terms like cosine theta can simplify the conversion process.
The identity sine theta / cosine theta is equivalent to tangent theta, which can be expressed as y/x.
Multiplying by r can sometimes be avoided by first addressing fractions or identities within the equation.
Changing reciprocal functions like cosecant or secant to their trigonometric equivalents simplifies the equation.
r = 3 cosecant theta simplifies to a horizontal line at y = 3 after converting to rectangular form.
Multiplying by r^3 can help create x and y terms from r terms in more complex polar equations.
When converting r = sin(θ)cos^2(θ), multiplying by r^3 and then applying trigonometric identities leads to a solvable rectangular equation.
The choice between different methods of conversion should be guided by which approach leads to the simplest rectangular form.
r = 2 represents a circle with a radius of two in polar coordinates, which converts to x^2 + y^2 = 4 in rectangular coordinates.
Complex polar equations like r - r*cos(θ) = 4 can be simplified by addressing fractions and then converting to rectangular form.
The final rectangular form may be a conic section, such as a parabola, which is a shift from the polar form's representation.
Transcripts
Browse More Related Video
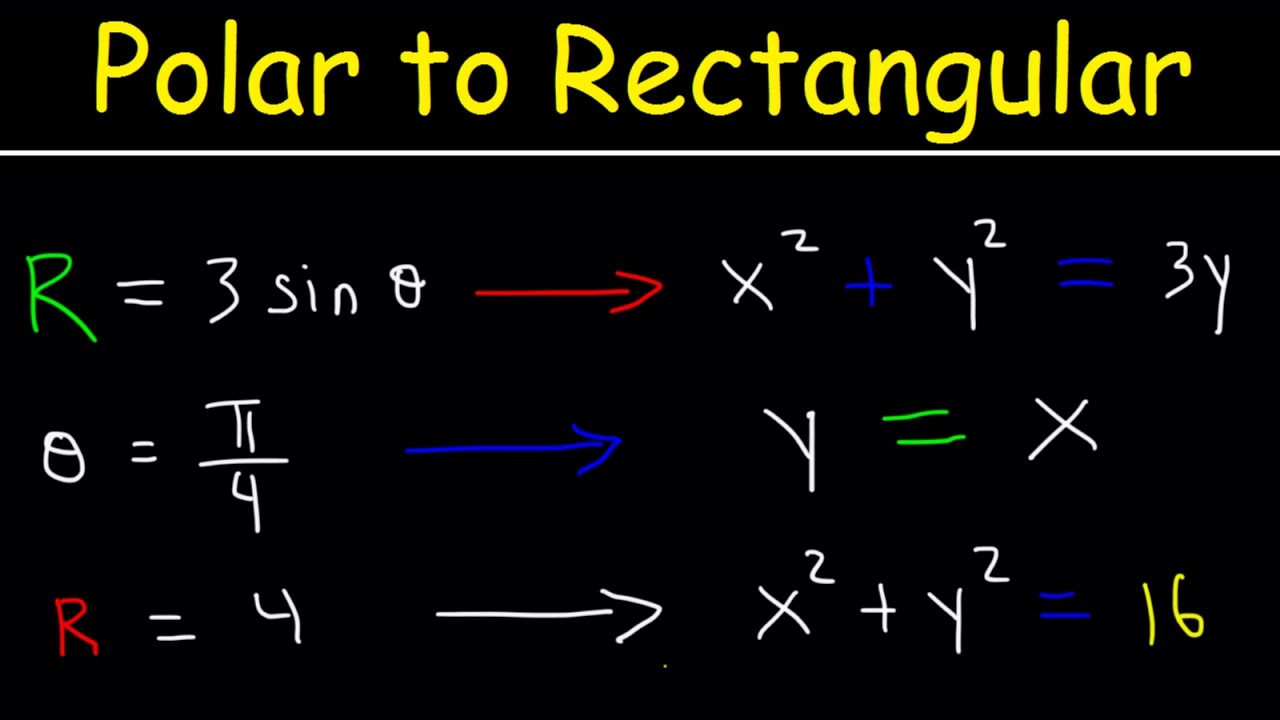
Polar Equations to Rectangular Equations, Precalculus, Examples and Practice Problems

Rectangular Equation to Polar Equations, Precalculus, Examples and Practice Problems
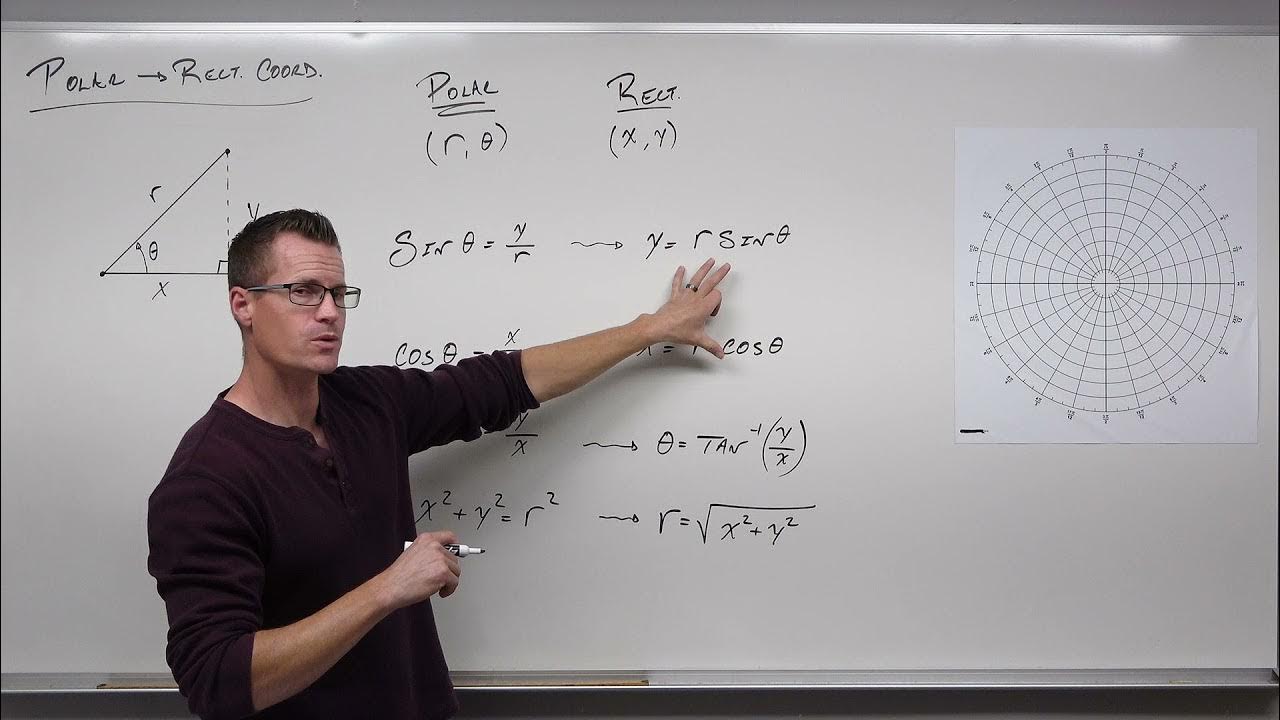
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

How to Convert From Rectangular Coordinates to Polar Coordinates (Precalculus - Trigonometry 38)
5.0 / 5 (0 votes)
Thanks for rating: