Law of Cosines, Finding Angles & Sides, SSS & SAS Triangles - Trigonometry

The Organic Chemistry Tutor
22 Oct 201710:17
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script demonstrates the process of solving triangles using the Law of Cosines and the Law of Sines. It begins with a scenario where sides a and b, and angle c are given, explaining why the Law of Sines is inapplicable and the Law of Cosines is the correct choice. The script then guides through calculating side c and subsequently finding angles a and b using the Law of Sines. Another example with all sides known is used to illustrate the use of the Law of Cosines to find angle c, followed by the other angles using the Law of Sines. The lesson emphasizes the importance of selecting the appropriate trigonometric law based on the given information and concludes with a clear explanation of how to find all angles and sides of a triangle.

Takeaways
  • 📐 **Solving Triangles with SAS:** When you have a side, an angle, and another side (SAS) in a triangle, you cannot use the Law of Sines directly because you don't have two sides with the same angle.
  • ❌ **Law of Sines Limitation:** The Law of Sines cannot be used when you have all different letters for sides and angles in the triangle.
  • 📐 **Using Law of Cosines:** The Law of Cosines is applicable when you have SAS in a triangle and is used to find the unknown side.
  • 🔢 **Law of Cosines Formula:** The formula for Law of Cosines is c^2 = a^2 + b^2 - 2ab * cos(C), where a, b, and c are the sides of the triangle, and C is the angle opposite to side c.
  • 🔢 **Alternative Formulas:** There are three forms of the Law of Cosines, but you can use any that provides the known values needed for calculation.
  • 🛰️ **Finding Side C:** Given sides a and b, and angle C, you can find the unknown side c using the Law of Cosines.
  • 🔄 **Applying Law of Sines After Finding Side C:** Once side c is found, you can use the Law of Sines to find the other angles in the triangle.
  • 🔢 **Law of Sines Formula:** The Law of Sines formula is a/sin(A) = b/sin(B) = c/sin(C), which can be used to find angles once all sides are known.
  • 🔢 **Calculating Angle B:** With side c and angle C known, you can find angle B using the Law of Sines by setting c/sin(C) = b/sin(B).
  • 🔄 **Finding Angle A:** After finding angle B, you can determine angle A by subtracting the known angles from 180 degrees, as the sum of angles in a triangle is always 180 degrees.
  • ⚖️ **Right Triangle Scenario:** If the triangle turns out to be a right triangle, the process simplifies because one angle is 90 degrees.
  • 📐 **SSS Triangle Solution:** When you have all three sides of a triangle (SSS), you use the Law of Cosines to find the first angle, and then the Law of Sines to find the remaining angles.
Q & A

  • What is the first step in solving a triangle when given two sides and the included angle?

    -The first step is to draw the triangle and identify the given sides and angle. In this case, side a is 10, side b is 20, and angle c is 60 degrees.

  • Why can't the Law of Sines be used directly with the given triangle?

    -The Law of Sines cannot be used directly because it requires two sides and their opposite angles to be known. Here, we have sides a and b, but we don't have angle a or angle b.

  • What law is suggested to use instead of the Law of Sines for this triangle?

    -The Law of Cosines is suggested to use because it can be applied when we have two sides and the included angle, which is the case here.

  • What is the formula of the Law of Cosines used to find side c?

    -The formula used is c^2 = a^2 + b^2 - 2ab * cos(angle c), where a and b are the given sides, and angle c is the given angle.

  • How do you calculate the value of side c using the Law of Cosines?

    -You substitute the given values into the formula: c^2 = 10^2 + 20^2 - 2*10*20*cos(60). Then you calculate the result to find c, which is the square root of the calculated value.

  • What is the value of side c after applying the Law of Cosines?

    -After applying the Law of Cosines, side c is calculated to be approximately 17.32 units.

  • Once side c is found, how can the Law of Sines be used to find the other angles?

    -The Law of Sines can be used by setting up a proportion with the known sides and their opposite angles, such as c/sin(c) = b/sin(b) to find angle b.

  • What is the value of angle b after using the Law of Sines?

    -Angle b is found to be 90 degrees after using the Law of Sines.

  • How can you find angle a after knowing angle b?

    -Angle a can be found by subtracting the known angles from 180 degrees: 180 - 90 - 60, which gives angle a as 30 degrees.

  • What is the significance of the triangle being a right triangle in this context?

    -The significance is that once angle b is found to be 90 degrees, it confirms that the triangle is a right triangle, simplifying the process of finding the remaining angles.

  • In the second example with sides 7, 8, and 9, how is the Law of Cosines used to find angle c?

    -The Law of Cosines is used by rearranging the formula to solve for cosine of angle c: cos(c) = (c^2 - a^2 - b^2) / (-2ab), and then finding the angle by taking the arccosine of the result.

  • What is the approximate value of angle c for the second triangle with sides 7, 8, and 9?

    -The approximate value of angle c is 73.4 degrees.

  • How can you determine the other angles once angle c is found using the Law of Cosines?

    -Once angle c is found, you can use the Law of Sines to find the other angles by setting up proportions with the known sides and their opposite angles.

  • What is the value of angle a after using the Law of Sines in the second example?

    -Angle a is found to be approximately 48.2 degrees.

  • How is angle b calculated in the second example?

    -Angle b is calculated by subtracting the known angles from 180 degrees: 180 - 73.4 - 48.2, which gives angle b as approximately 58.4 degrees.

Outlines
00:00
📐 Solving a SAS Triangle Using the Law of Cosines

This paragraph explains how to solve a side-angle-side (SAS) triangle when given two sides and the included angle. The example triangle has sides A=10, B=20, and angle C=60 degrees. The presenter clarifies that the Law of Sines cannot be used due to the lack of corresponding angles and instead uses the Law of Cosines. The formula c² = a² + b² - 2ab*cos(C) is applied, where a and b are known sides and C is the known angle. The calculation leads to finding side C as 10√3 or approximately 17.32 units. After determining side C, the Law of Sines is then used to find angle B, which turns out to be 90 degrees, and subsequently angle A is found to be 30 degrees, confirming the triangle is a right triangle.

05:00
📏 Analyzing a Right Triangle with the Law of Cosines

In this paragraph, the script discusses solving a right triangle given all three sides: A=7, B=8, and C=9. The Law of Cosines is used to find the measure of angle C. The formula cos(C) = (c² - a² - b²) / (-2ab) is rearranged and applied, leading to the calculation of cos(C) as 2/7 or approximately 0.2857. The arccosine of this value gives angle C as approximately 73.4 degrees. The Law of Sines is then used to find angle A, resulting in approximately 48.2 degrees. Since the sum of angles in a triangle must be 180 degrees, angle B is calculated as 180 - 73.4 - 48.2, which equals 58.4 degrees. The paragraph emphasizes that when all three sides are known, the Law of Cosines should be used first to find an angle, after which the Law of Sines can be used to find the remaining angles.

Mindmap
Keywords
💡Law of Sines
The Law of Sines is a trigonometric formula that relates the lengths of the sides of a triangle to the sines of its angles. It is used to solve triangles when two angles and one side are known, or when two sides and an angle not included between them are known. In the video, it is initially considered for use but is found to be unsuitable due to the lack of two sides with the same corresponding angles, which is a requirement for its application.
💡Law of Cosines
The Law of Cosines is another trigonometric formula that relates the sides of a triangle to the cosine of one of its angles. It is particularly useful for solving triangles when the lengths of all three sides are known (SSS case), or when two sides and a non-included angle are known (SAS case). In the video, the Law of Cosines is used to find the unknown side of a triangle when two sides and the included angle are known.
💡Side-Angle-Side (SAS)
Side-Angle-Side (SAS) is a condition in trigonometry where two sides and the included angle of a triangle are given. The SAS condition is used to determine the remaining sides and angles of the triangle. In the video, the SAS condition is mentioned in the context of when the Law of Sines can be applied, but it is not applicable in the given scenario because the known angle is not included between the two known sides.
💡Angle C
In the context of the video, Angle C is one of the angles of the triangle being solved. It is given as 60 degrees in the first example and 73.4 degrees in the second example. The angle is used in conjunction with the Law of Cosines to find the unknown side of the triangle.
💡Side A and Side B
Side A and Side B are the two known sides of the triangle in the video's first example, where Side A is 10 and Side B is 20. These sides, along with the known angle, are used to apply the Law of Cosines to find the unknown side of the triangle.
💡Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, the theorem is implicitly used when applying the Law of Cosines to find that the triangle is a right triangle.
💡Arc Sine
The arc sine, often abbreviated as sin^(-1) orasin, is the inverse function of the sine function. It is used to find the angle whose sine is a given number. In the video, the arc sine is used to find Angle B and Angle A after the unknown side has been calculated using the Law of Cosines.
💡Right Triangle
A right triangle is a triangle in which one of the angles is a right angle (90 degrees). In the video, after calculating the angles using the Law of Sines and the Law of Cosines, it is determined that the triangle in the first example is a right triangle because one of its angles is 90 degrees.
💡Sine Function
The sine function is a trigonometric function of an angle, important in mathematics and physics for its wide-ranging applications, from simple calculations involving lengths and angles to modeling periodic phenomena. In the video, the sine function is used in the context of the Law of Sines to find the unknown angles of the triangle.
💡Cosine Function
The cosine function, like the sine function, is a trigonometric function that describes a certain ratio in a right-angled triangle. It is used in the Law of Cosines to relate the sides of a triangle to the cosine of one of its angles. In the video, the cosine function is used to calculate the unknown angles of the triangle after finding the unknown side.
💡Sum of Angles in a Triangle
The sum of the angles in any triangle always equals 180 degrees. This property is used in the video to find the third angle of the triangle when two angles are known, by subtracting the known angles from 180 degrees.
Highlights

Introduction to solving a triangle with given side and angle using the Law of Cosines.

Explanation of why the Law of Sines is not applicable in a side-angle-side scenario.

Demonstration of the Law of Cosines formula and its rearrangement for different sides and angles.

Step-by-step calculation to find side c using the given sides a and b, and angle C.

Conversion of angle measurements from degrees to cosine values for calculation.

Finding the length of side c using the Law of Cosines with a = 10, b = 20, and angle C = 60 degrees.

Transition from Law of Cosines to Law of Sines to find the remaining angles of the triangle.

Calculation of angle B using the Law of Sines and the known sides and angle C.

Determination of angle A by subtracting the known angles from 180 degrees.

Conclusion that the triangle is a right triangle based on the calculated angles.

Introduction of a second example with sides a = 7, b = 8, and c = 9.

Application of the Law of Cosines to find angle C with all sides known.

Detailed calculation of cosine of angle C using the rearranged Law of Cosines formula.

Conversion of the cosine value to angle C in degrees.

Use of the Law of Sines to find angle A with the calculated angle C and side a.

Calculation of angle B by subtracting the other angles from 180 degrees.

Final summary of the process to solve triangles using the Law of Cosines and Law of Sines.

Transcripts

Browse More Related Video

The Law of Sines

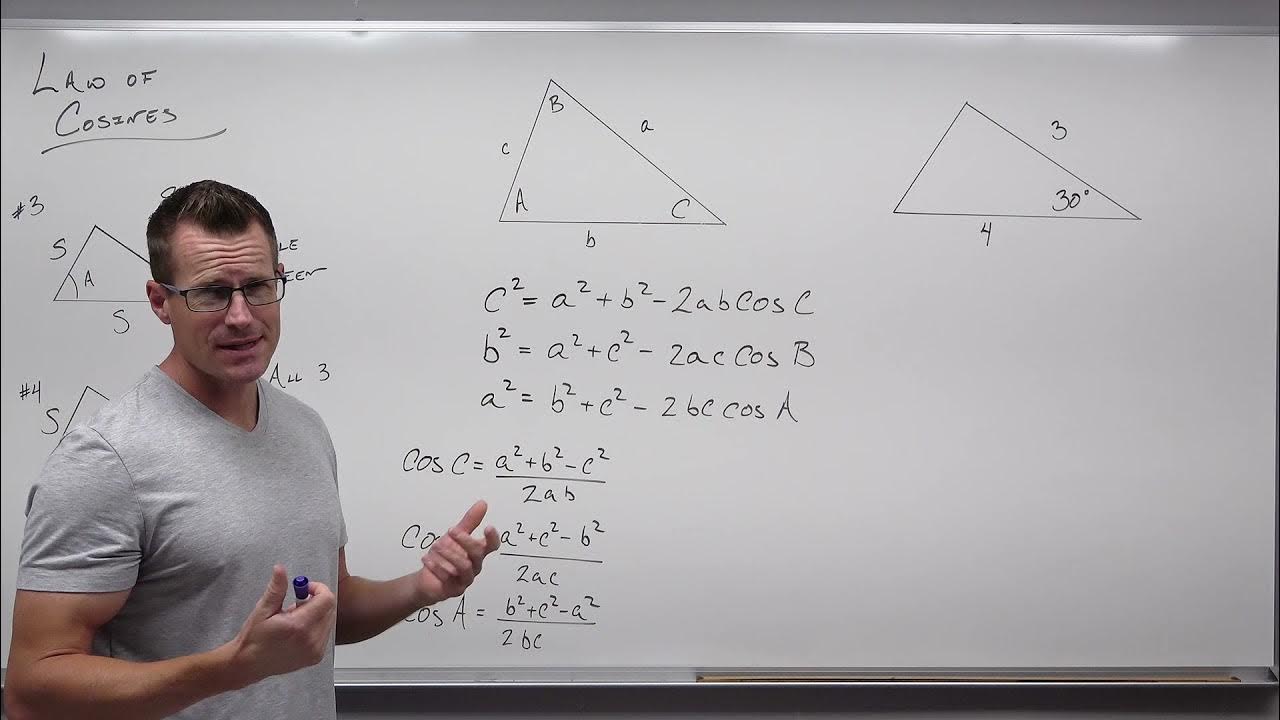
How to Use the Law of Cosines in Trigonometry (Precalculus - Trigonometry 33)

The Law of Cosines

How to Use the Law of Sines in Trigonometry (Precalculus - Trigonometry 32)

Law of Sines, Basic Introduction, AAS & SSA - One Solution, Two Solutions vs No Solution, Trigonomet

Law of Sines - Basic Introduction

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Triangle LawMathematicsEducationalLaw of CosinesLaw of SinesGeometryProblem SolvingTrigonometryRight TriangleMath Guide