Law of Sines, Basic Introduction, AAS & SSA - One Solution, Two Solutions vs No Solution, Trigonomet

The Organic Chemistry Tutor

21 Oct 201721:12

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script introduces the Law of Sines, a fundamental principle for solving triangles. It explains the formula relating the sides of a triangle to the sines of their opposite angles, demonstrating how to find missing angles and sides. The script walks through several examples, including scenarios with SSA (Side-Side-Angle) triangles where multiple solutions may exist. It also emphasizes the importance of checking solutions for validity, ensuring they form a valid triangle with angles summing to 180 degrees. The lesson is designed to help viewers understand and apply the Law of Sines in various triangle problems.

Takeaways

📚 The Law of Sines is a formula used to find missing angles or sides in a triangle.
🔍 The formula is given by \( \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \), where \( a \), \( b \), and \( c \) are the sides opposite to angles \( A \), \( B \), and \( C \) respectively.
✅ The sum of the angles in any triangle always adds up to 180 degrees.
📝 To solve a triangle, one can start by finding the missing angles using the sum of angles property and then apply the Law of Sines to find the missing sides.
📉 When using the Law of Sines, only two fractions of the three are needed at any given moment to solve for the unknowns.
🧭 To find an unknown side, cross-multiply the equation and isolate the unknown side variable.
📲 Ensure your calculator is in degree mode when using trigonometric functions to avoid incorrect results.
🔢 Use the inverse sine function (arc sine) to find the measure of an angle when given the ratio of the side to the sine of the angle.
⚠️ Be aware that the sum of any two angles in a triangle must be less than 180 degrees, otherwise, the triangle is not possible.
🤔 In some cases, especially with SSA (side-side-angle) triangles, there may be two possible solutions for the triangle.
📐 When checking the validity of a solution, consider the relationship between the side lengths and their opposite angles; the longest side should be opposite the largest angle.

Q & A

What is the Law of Sines?
-The Law of Sines is a formula that relates the ratios of the lengths of sides of a triangle to the sines of its angles. It states that the ratio of a side length to the sine of its opposite angle is constant for all three sides of a triangle.
How can the Law of Sines be used to find missing angles or sides in a triangle?
-The Law of Sines can be used to find missing angles or sides by setting up equations based on the known angles and sides. By comparing the ratios of the sides to the sines of their opposite angles, you can solve for the unknown elements of the triangle.
What is the sum of the angles in any triangle?
-The sum of the angles in any triangle is always 180 degrees.
In the example where angle A is 60 degrees and angle B is 70 degrees, what is the measure of angle C?
-To find angle C, you subtract the sum of angles A and B from 180 degrees. So, angle C = 180 - (60 + 70) = 180 - 130 = 50 degrees.
How do you use the Law of Sines to find side B when angle A is 60 degrees, angle B is 70 degrees, and side A is 8 units?
-You use the Law of Sines formula: a/sinA = b/sinB. Plugging in the known values, you get 8/sin(60) = b/sin(70). Cross-multiplying and solving for b gives you b = 8 * sin(70) / sin(60), which equals approximately 8.68 units.
What is the value of side C when angle A is 60 degrees, angle C is 50 degrees, and side A is 8 units?
-Using the Law of Sines, a/sinA = c/sinC, you get 8/sin(60) = c/sin(50). Solving for c gives you c = 8 * sin(50) / sin(60), which equals approximately 7.07 units.
What is an SSA triangle and why is it important to consider multiple solutions when solving it?
-An SSA triangle is one where you know two sides and the angle opposite one of them. It's important to consider multiple solutions because the Law of Sines can sometimes yield two different angles for the unknown angle, leading to two possible triangles.
How do you determine if there is one or two possible triangles when solving an SSA triangle?
-You determine the number of possible triangles by finding the supplementary angle to the calculated angle and adding it to the known angles. If the sum is less than 180 degrees, there can be two triangles; if it equals or exceeds 180 degrees, there is only one solution.
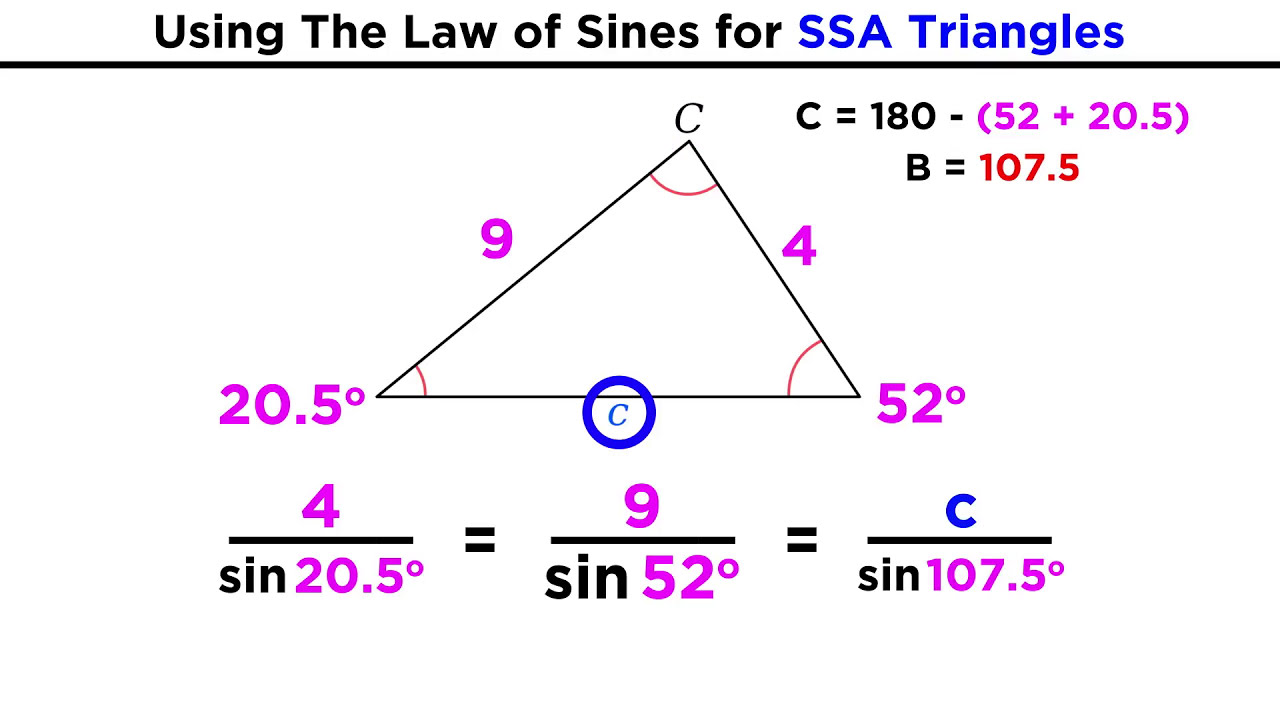
In the example where angle A is 42 degrees, side A is 10, and side B is 9, how do you find angle B?
-Using the Law of Sines, a/sinA = b/sinB, you set up 10/sin(42) = 9/sinB. Cross-multiplying gives you 9 * sin(42) = 10 * sin(B). Solving for B involves taking the arcsine (inverse sine) of 0.602, which gives you angle B approximately 37.03 degrees.
Why is it not possible to find angle C when angle A is 75 degrees, side A is 8, and side C is 9?
-When you attempt to use the Law of Sines to find angle C, you get a sine value greater than 1, which is not possible since the sine of an angle cannot exceed 1. This indicates that no such triangle exists with the given measurements.
How do you check if your answers for the sides of a triangle make sense?
-You can check if your answers make sense by comparing the length of the sides to the size of the opposite angles. The smallest side should be opposite the smallest angle, and the largest side should be opposite the largest angle.

Outlines

00:00

📚 Introduction to the Law of Sines

This paragraph introduces the Law of Sines, a mathematical formula used to solve triangles. It explains the notation where uppercase letters represent angles and lowercase represent side lengths. The formula is given as side a over sine of angle a equals side b over sine of angle b, which equals side c over sine of angle c. The paragraph also reminds us that the sum of angles in a triangle must be 180 degrees. An example is provided where angles a and b, and side a are given, and the task is to find the missing angle c, side b, and side c. The process involves calculating angle c first, then using the Law of Sines to find the lengths of sides b and c.

05:07

🔍 Solving Triangles Using the Law of Sines

This paragraph continues the discussion on solving triangles with the Law of Sines. It presents a scenario with a side-side-angle (SSA) triangle where angle a is 42 degrees, side a is 10, and side b is 9. The goal is to find angle b using the Law of Sines, which involves cross-multiplying and using the inverse sine function. The paragraph also addresses the possibility of multiple solutions when using the inverse sine function, but clarifies that only one solution is valid if the sum of angles a and b is less than 180 degrees. The process includes finding angle c and the missing side c using the Law of Sines.

10:10

📐 Validating Triangle Solutions with the Law of Sines

This paragraph emphasizes the importance of validating the solutions obtained from the Law of Sines. It provides an example of an SSA triangle with angle a as 75 degrees, side a as 8, and side c as 9. The process of finding angle c involves using the Law of Sines and the inverse sine function. However, when attempting to find angle c using a sine value greater than 1, it indicates that no solution exists for the triangle. The paragraph also discusses the relationship between side lengths and angles, suggesting that the smallest side should be opposite the smallest angle, which can be a quick check for the validity of the solution.

15:12

🤔 Handling Multiple Solutions in Triangle Problems

This paragraph explores the concept of multiple solutions when solving triangle problems with the Law of Sines. It provides an example with angle a as 30 degrees, side a as 7, and side b as 8. The process involves finding angle b using the Law of Sines and then determining if a second solution is possible by subtracting the found angle from 180 degrees. If the sum of the existing angle and the supplementary angle is less than 180 degrees, two triangles are possible. The paragraph concludes by calculating side c for both potential triangles and using the relationship between side lengths and angles to validate the solutions.

20:12

🔄 Understanding the Conditions for Multiple Triangle Solutions

The final paragraph summarizes the conditions for determining whether there is one or two possible solutions when solving triangles. It explains that after finding an angle, one should find its supplementary angle by subtracting from 180 degrees. If the sum of the original angle and the supplementary angle is less than 180 degrees, two triangles are possible. If the sum is greater than or equal to 180 degrees, only one triangle can be formed. This paragraph reinforces the importance of checking the sum of angles to ascertain the validity of the solutions obtained.

Mindmap

Keywords

💡Law of Sines

The Law of Sines is a fundamental principle in trigonometry that relates the ratios of the lengths of sides of a triangle to the sines of its angles. In the video, it is the primary tool used to solve for missing angles and sides of a triangle. The formula is given as \( \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \), where 'a', 'b', and 'c' are the side lengths opposite to angles 'A', 'B', and 'C', respectively. This law is essential for solving various types of triangles, especially when two angles and one side are known.

💡Triangle

A triangle is a three-sided polygon with three angles that always add up to 180 degrees. In the context of the video, different types of triangles are discussed, such as those with given angles and sides, and the process of solving them using the Law of Sines is demonstrated. The script provides examples of solving for missing angles and sides in various scenarios, emphasizing the importance of triangles in trigonometry.

💡Angle

An angle in the video script refers to the measure of the space between two lines or rays that intersect at a common point, known as the vertex. Angles are fundamental in the study of triangles and are used to apply the Law of Sines. The script mentions specific angles like angle 'a' being 60 degrees and angle 'b' being 70 degrees, which are then used to find the third angle and the missing sides of the triangle.

💡Side

In the context of the video, a side of a triangle is the line segment connecting two vertices. The script explains how to find the lengths of missing sides using the Law of Sines once the angles are known. For example, with angle 'a' and side 'a' given, the script demonstrates how to calculate side 'b' and side 'c'.

💡Sine

The sine function is a trigonometric function that in the context of the video, is used to relate the ratio of the opposite side to an angle in a right-angled triangle. The script uses sine values to solve for unknown sides and angles using the Law of Sines, such as calculating \( \sin B \) when finding side 'b'.

💡Cross Multiply

Cross multiplying is a method used in algebra to solve equations involving fractions. In the video, this technique is applied when using the Law of Sines to isolate and solve for an unknown side or angle. For instance, when finding side 'b', the script cross multiplies to get \( 8 \sin 70^\circ = b \sin 60^\circ \) and then solves for 'b'.

💡Inverse Sine (Arcsine)

The inverse sine function, or arcsine, is the reverse of the sine function and is used to find an angle when the sine value is known. In the script, arcsine is used to determine angles 'b' and 'c' after calculating their sine values using the Law of Sines. For example, to find angle 'b', the script uses \( \sin^{-1}(0.602) \) to get an angle of approximately 37 degrees.

💡SSA Triangle

An SSA triangle refers to a situation where two sides and the angle opposite one of them are known, but not the angle between the two known sides. The script discusses the SSA case and how it can lead to either one or two possible triangles, depending on the sum of the angles. This is demonstrated when angle 'a' is 42 degrees, side 'a' is 10, and side 'b' is 9, leading to a calculation that could potentially result in two triangles.

💡Supplementary Angle

A supplementary angle is one that, when added to another angle, equals 180 degrees. In the video, the concept is used to find a second possible angle when solving an SSA triangle. The script explains that by subtracting an angle from 180 degrees, you can find a supplementary angle that might lead to a second solution for the triangle.

💡Radian Mode

Radian mode refers to the setting on a calculator that uses radians instead of degrees for trigonometric calculations. The script mentions that it's important to ensure the calculator is set to degree mode when solving problems involving angles in degrees, as using radian mode would yield incorrect results.

Highlights

Introduction to the Law of Sines and its formula for solving triangles.

Explanation of the relationship between angles and side lengths in a triangle using the Law of Sines.

The necessity for the sum of angles in a triangle to equal 180 degrees.

Step-by-step example to solve a triangle given two angles and one side.

Calculation of the missing angle using the sum of angles in a triangle.

Use of the Law of Sines to find missing sides in a triangle.

Cross-multiplication method to solve for an unknown side.

Importance of checking calculator settings for degree or radian mode.

Demonstration of solving for side lengths using the Law of Sines.

Explanation of the SSA (Side-Side-Angle) triangle scenario.

Process of finding an angle using the inverse sine function.

Consideration of multiple solutions when using the inverse sine function.

Criteria for determining the number of possible triangles in an SSA case.

Verification of triangle solutions by checking the sum of angles.

Method to find the missing side in an SSA triangle using the Law of Sines.

Illustration of checking the sensibility of answers by comparing angles and sides.

Example of an SSA triangle with no solution due to the sine value exceeding the range.

Approach to solving triangles with two possible solutions.

Technique for calculating supplementary angles to find the second triangle.

Final verification of the sensibility of solutions by comparing side lengths to angles.

Transcripts

Browse More Related Video

How to Use the Law of Sines in Trigonometry (Precalculus - Trigonometry 32)

The Law of Sines

Law of Sines - Basic Introduction

Law of Cosines, Finding Angles & Sides, SSS & SAS Triangles - Trigonometry

How To Calculate The Missing Angle In a Triangle

How to Use the Law of Cosines in Trigonometry (Precalculus - Trigonometry 33)

Related Tags

Law of Sines Triangle Solving Mathematics Trigonometry Problem Solving Educational Geometry Angle Calculation Side Lengths SSA Triangles