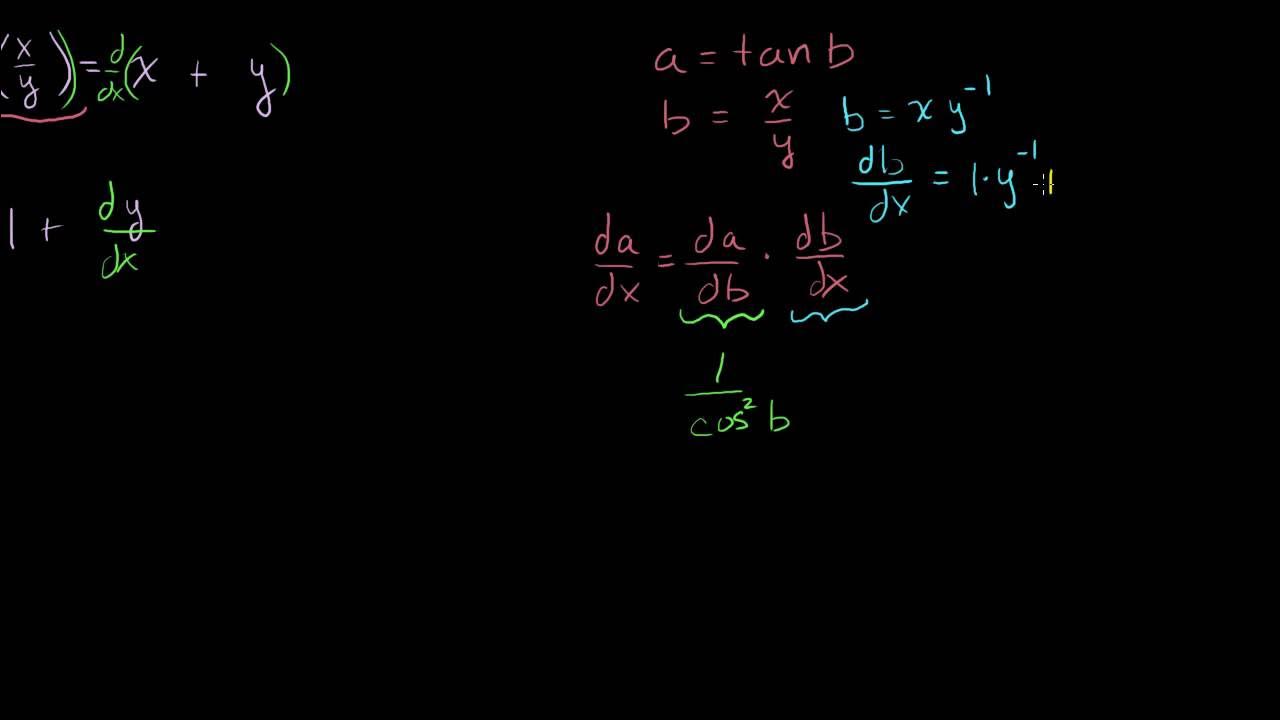More implicit differentiation
TLDRThe video script provides a detailed walkthrough of implicit differentiation, a technique used in calculus to find the derivative of a function when it is not explicitly defined. The presenter tackles two complex problems, carefully explaining each step and clarifying common points of confusion. The first problem involves a quadratic equation in x and y, while the second is a simpler polynomial equation. By applying the chain rule and derivative properties, the presenter successfully derives the expressions for dy/dx, offering insights into the process and emphasizing the importance of understanding the underlying rules.
Takeaways
- 📚 Implicit differentiation is a technique used to find the derivative of a function when the relationship between variables is not explicitly expressed.
- 🤔 The process can be confusing, but it is essentially about finding the rate of change of one variable with respect to another when given an implicit function.
- 🧠 Start by differentiating both sides of the equation with respect to the variable you are differentiating with respect to, in this case, x.
- 📈 Use the chain rule when differentiating products or composite functions, remembering that the derivative of y with respect to x is denoted as dy/dx or y'.
- 🌟 For the given function x^2 - 24xy + 16y^2 - 400x - 300y = 0, differentiate each term carefully, separating the y' terms from the non-y' terms.
- 🔄 After differentiation, collect like terms and isolate the y' terms on one side of the equation to solve for dy/dx.
- 📝 For the second problem x - y^2 = 8y - 6, apply the same process, using the chain rule for the term involving y and simplifying the equation to solve for dy/dx.
- 👉 The derivative of y with respect to x for the first function is given by (12y - x + 200) / (16y - 12x - 150), and for the second function, it is (y - x) / (y - x - 8).
- 💡 Implicit differentiation is a powerful tool that allows us to find the slope of a curve at any point, even when the equation is not easily solved for y.
- 📊 Always check your work for any mistakes, as even small errors can lead to incorrect results in the derivative.
- 🎓 Practice is key in mastering implicit differentiation, so solving multiple problems will help solidify understanding and application.
Q & A
What is the main topic of the video script?
-The main topic of the video script is implicit differentiation, a method used in calculus to find the derivative of a function when it is not explicitly defined.
What is the implicit function given in the script?
-The implicit function given in the script is x^2 - 24xy + 16y^2 - 400x - 300y = 0.
How does the process of implicit differentiation begin?
-The process of implicit differentiation begins by taking the derivative of both sides of the given equation with respect to x.
What is the significance of the 'y prime' notation used in the script?
-The 'y prime' notation is used to represent dy/dx, the derivative of y with respect to x. It is an alternative to the traditional notation to help viewers get used to different types of notation in calculus.
What is the product rule mentioned in the script, and when is it applied?
-The product rule is a fundamental calculus rule used to find the derivative of a product of two functions. In the script, it is applied when differentiating the term xy with respect to x.
How is the derivative of y with respect to x represented in the final answer of the first problem?
-In the final answer of the first problem, the derivative of y with respect to x is represented as (12y - x + 200) / (16y - 12x - 150).
What is the second implicit function provided in the script?
-The second implicit function provided in the script is x - y^2 = 8y - 6.
How is the derivative of the right-hand side of the second equation found?
-The derivative of the right-hand side of the second equation is found by recognizing that the constant term (6) does not contribute to the derivative, and the derivative of 8y with respect to x is 8 times the derivative of y with respect to x (dy/dx).
What is the final expression for the derivative of y with respect to x in the second problem?
-The final expression for the derivative of y with respect to x in the second problem is (y - x) / (y - x - 8).
What is the purpose of the video script in teaching implicit differentiation?
-The purpose of the video script is to provide a clear and detailed explanation of the process of implicit differentiation, helping viewers understand how to find the derivative of a function when it is not explicitly given, and how to apply the chain rule and product rule in this context.
How does the script emphasize the importance of understanding the chain rule in implicit differentiation?
-The script emphasizes the importance of understanding the chain rule by explaining that when differentiating terms involving y, one must take the derivative with respect to y and then multiply by the derivative of y with respect to x (dy/dx or y prime). This highlights that the chain rule is being applied, even when people might simply memorize the process without understanding the underlying principle.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, acknowledging that it can be a challenging topic for many. The speaker explains the process of differentiating both sides of an equation with respect to x, using an example where the equation is x^2 - 24xy + 16y^2 - 400x - 300y = 0. The explanation includes taking the derivative of each term, applying the product rule, and chain rule where necessary. The focus is on understanding the process and notation, including the use of 'y prime' as an alternative to dy/dx, emphasizing the importance of recognizing the chain rule when differentiating y with respect to x.
🔢 Deriving the Implicit Function for the First Equation
In this paragraph, the speaker continues the process of implicit differentiation for the given equation. The focus is on isolating the terms with 'y prime' (dy/dx) and simplifying the equation. The speaker carefully takes the derivative of each term, applies the chain rule for terms involving y, and combines like terms. The result is an equation that expresses the derivative of y with respect to x in terms of x and y. The speaker also emphasizes the importance of writing dy/dx explicitly to remind oneself of the chain rule application and concludes with a simplified form of the derivative.
📈 Solving the Second Implicit Differentiation Problem
The speaker moves on to a second, seemingly simpler implicit differentiation problem, involving the equation x - y^2 = 8y - 6. The process involves taking the derivative of both sides with respect to x, applying the chain rule for the term involving y, and solving for dy/dx. The speaker provides a step-by-step breakdown of the differentiation process, including the handling of constants and the final algebraic manipulation to isolate dy/dx. The result is a neat expression for the derivative of y with respect to x, showcasing the ability to handle complex implicit functions and extract meaningful information about the slope of the function at any point.
Mindmap
Keywords
💡Implicit Differentiation
💡Derivative
💡Chain Rule
💡Product Rule
💡Slope
💡Equation
💡Constant
💡Notation
💡Simplify
💡视频中的示例
💡导数的求解
Highlights
Introduction to implicit differentiation and its common challenges.
The given implicit function: x^2 - 24xy + 16y^2 - 400x - 300y = 0.
Derivative process explained, including the use of the product and chain rules.
Explanation of the derivative of xy, using both the product rule and the concept of dy/dx.
Clarification on the importance of understanding the chain rule when differentiating y with respect to x.
Rearrangement of terms and separation of y prime terms for simplification.
Solution for the derivative equation, expressed as a ratio of two polynomials in y and x.
The second problem presented: x - y^2 = 8y - 6.
Derivative of the given equation using the chain rule and the concept of dy/dx.
Solving for dy/dx by isolating and distributing terms.
Final answer for the second problem, expressed as a rational function of y and x.
Emphasis on the practical application of implicit differentiation in finding the slope of a curve at any point.
The use of different notations (y prime and dy/dx) to express derivatives and their implications.
The process of moving terms to one side of the equation to isolate dy/dx.
The simplification of the final derivative expression by dividing both the numerator and the denominator by common factors.
The demonstration of handling two distinct implicit functions and their respective differentiation processes.
The step-by-step breakdown of implicit differentiation, making complex concepts more accessible.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: