Inflection Points and Concavity Intuition

Khan Academy
22 Jan 201013:42
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of concavity in calculus, explaining the visual characteristics of functions that are concave upwards (like a U shape) and concave downwards (like an upside-down U). It further discusses inflection points as transition points between these two types of concavity. The relationship between the slope of a function and its concavity is explored, with the second derivative's role in indicating whether a function is concave up or down highlighted. The script aims to provide an intuitive understanding of these mathematical concepts and their implications.

Takeaways
  • 📈 The concept of concavity is important in calculus, referring to the curvature of a function's graph.
  • 📌 A graph that is concave upwards has a U-shape, indicating that the function's slope is increasing throughout its domain.
  • 📉 In contrast, a graph that is concave downwards resembles an upside-down U, where the function's slope is decreasing over the entire domain.
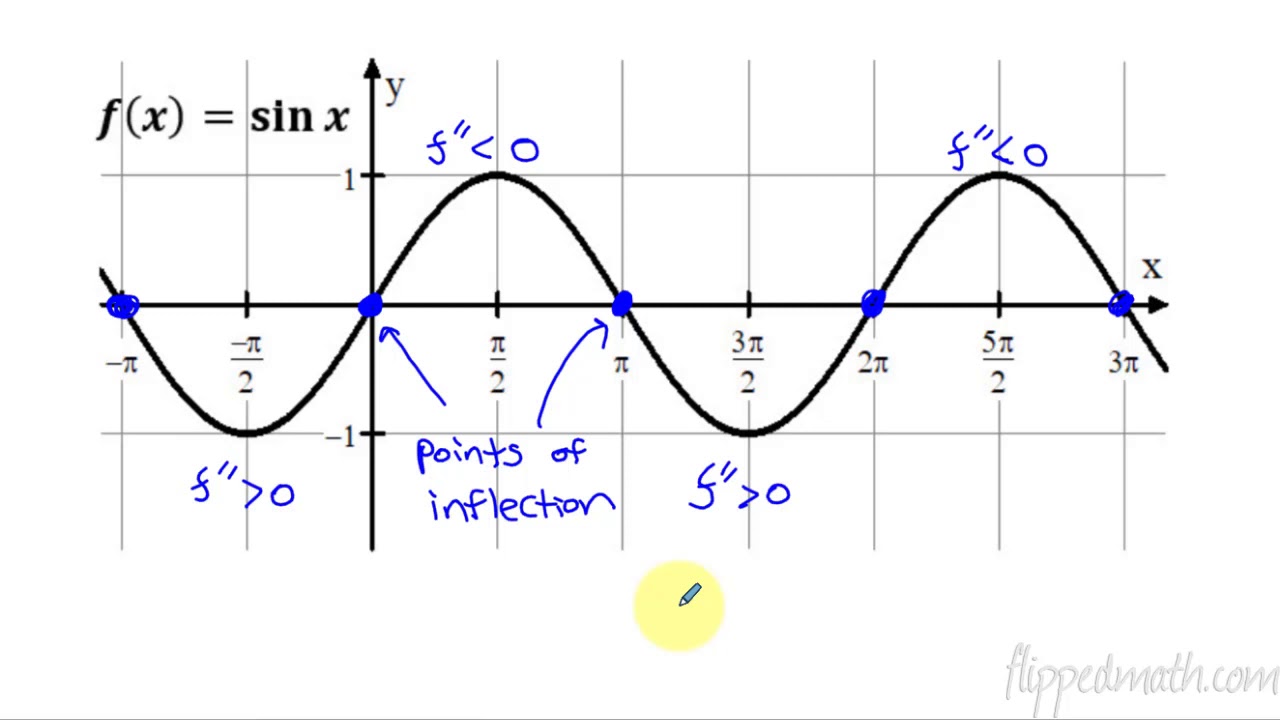
  • 🔄 Inflection points are transition points on a graph where the concavity changes from concave upwards to downwards or vice versa.
  • 🔽 At the inflection point, the slope of the tangent line to the graph (first derivative) is zero.
  • 📈 The second derivative represents the rate of change of the slope (first derivative), or the slope of the slope.
  • ⬆️ When a function is concave upwards, its second derivative is positive because the rate of change of the slope is increasing.
  • ⬇️ Conversely, when a function is concave downwards, its second derivative is negative as the rate of change of the slope is decreasing.
  • 🔄 At an inflection point, the second derivative must change signs, passing through zero, indicating a switch from positive to negative or negative to positive.
  • 💡 The presence of an inflection point can be confirmed by testing the second derivative around the point where it equals zero to ensure a sign change.
  • 📊 Visually identifying concavity and inflection points on a graph can provide an intuitive understanding of the function's behavior in terms of slope and curvature.
Q & A

  • What is the main topic discussed in the video?

    -The main topic discussed in the video is the concept of concavity in calculus, specifically focusing on concave upwards, concave downwards, and inflection points.

  • How can you visually identify a concave upwards function?

    -A concave upwards function can be visually identified by its graph, which has a shape resembling a 'U'. Over the entire domain of the function, it maintains this U shape, indicating that the function is concave upwards.

  • What does the term 'concave downwards' refer to?

    -The term 'concave downwards' refers to a graph that looks like an upside-down 'U'. This shape indicates that the function's graph is concave downwards over the interval where this shape is observed.

  • How does the slope of a concave upwards function behave?

    -In a concave upwards function, the slope increases throughout the interval. This means that as the value of x increases, the slope also increases, reflecting a positive rate of change of the slope.

  • What is the behavior of the slope in a concave downwards function?

    -In a concave downwards function, the slope decreases throughout the interval. This indicates that as the value of x increases, the slope becomes less positive, or more negative if it was negative to begin with, showing a negative rate of change of the slope.

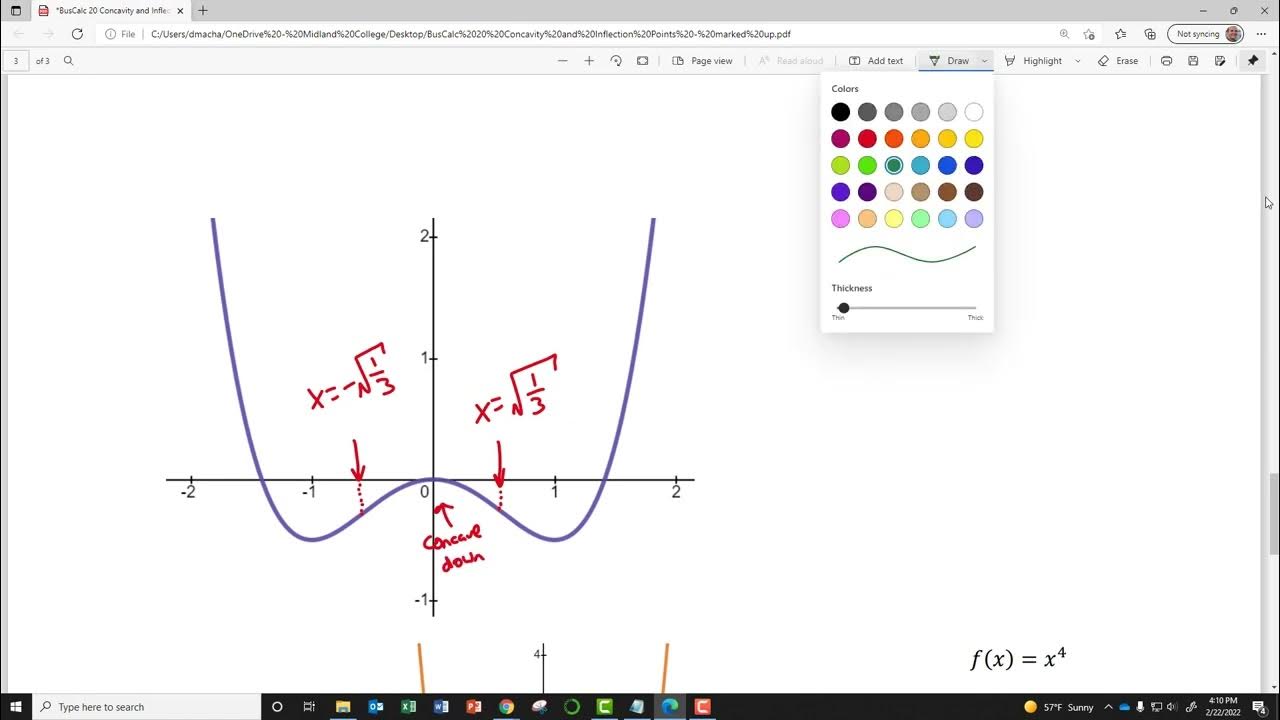
  • What is an inflection point in the context of the video?

    -An inflection point is a point on the graph of a function where the concavity changes, that is, where the function transitions from being concave upwards to concave downwards or vice versa. At an inflection point, the second derivative of the function is zero and potentially changes signs.

  • What does the second derivative represent in terms of the function's slope?

    -The second derivative represents the slope of the slope, or the rate of change of the slope itself. It provides information about how the slope of the function is changing, whether it is increasing (positive second derivative) or decreasing (negative second derivative).

  • How can you determine if a point is an inflection point based on the second derivative?

    -A point is determined to be an inflection point if the second derivative changes signs, either from positive to negative or from negative to positive, and the second derivative is zero at that point. This indicates a change in the rate of change of the slope, which is the characteristic of an inflection point.

  • What is the significance of the second derivative being greater than zero in a concave upwards function?

    -If the second derivative is greater than zero in a concave upwards function, it indicates that the rate of change of the slope is positive. This means that the slope of the function is increasing, which is consistent with the definition of a concave upwards interval.

  • What does a negative second derivative in a concave downwards function tell us?

    -A negative second derivative in a concave downwards function tells us that the rate of change of the slope is negative. This means that the slope of the function is decreasing, aligning with the definition of a concave downwards interval.

  • How can you differentiate between concave upwards and concave downwards just by looking at the graph?

    -You can differentiate between concave upwards and concave downwards by observing the shape of the graph. If the graph resembles a 'U' shape, it is concave upwards. If it resembles an upside-down 'U', it is concave downwards. The direction of the curvature in relation to the axis helps in identifying the type of concavity.

Outlines
00:00
📈 Introduction to Concavity and Inflection Points

This paragraph introduces the concepts of concavity and inflection points in the context of calculus. It explains that concavity refers to the curvature of a graph, with concave upwards resembling a 'U' shape and concave downwards being its opposite. The discussion then transitions to inflection points, which are points on a graph where the concavity changes from upwards to downwards or vice versa. The key idea is that at an inflection point, the graph transitions from one type of curvature to another, which can be analyzed by examining the behavior of the function's slope at different points.

05:02
📉 Analysis of Concave Downwards and Upwards

In this paragraph, the video script delves into the specifics of concave downwards and upwards by examining the behavior of a function's slope. It describes how the slope decreases as x increases in a concave downwards scenario, transitioning from a steep upward slope to a less steep one, eventually reaching a maximum point where the slope is zero. Conversely, in a concave upwards scenario, the slope increases as x increases, starting from a negative value, reaching zero at the minimum point, and then becoming increasingly positive. The summary emphasizes the visual recognition of these concavities and the implications they have on the slope of the function.

10:05
🔄 Relationship between Concavity and Second Derivative

The final paragraph of the script establishes the connection between concavity and the second derivative of a function. It explains that the second derivative represents the rate of change of the slope, or the slope of the slope. When a function is concave upwards, the slope is increasing, indicating a positive second derivative. Conversely, when a function is concave downwards, the slope is decreasing, which corresponds to a negative second derivative. The paragraph also discusses inflection points in relation to the second derivative, stating that an inflection point occurs when the second derivative crosses through zero, signifying a change in the sign of the rate of change of the slope. This is a crucial point for identifying where the concavity of a function changes.

Mindmap
Keywords
💡Concativity
Concativity refers to the shape or curvature of a graph, specifically whether it bends inwards or outwards relative to the axis. In the context of the video, it is used to describe the concave upwards and concave downwards characteristics of a function's graph. The term is crucial for understanding the behavior of a function, particularly in calculus, as it relates to the rate of change and the function's second derivative.
💡Concave Upwards
Concave upwards is a term used to describe a graph that curves in a U-shape, with both ends pointing upwards. It is a key concept in the video, as it indicates that the function's slope is increasing throughout its domain. An example from the video is a graph that consistently curves upwards, resembling a U, and this shape implies that the rate of change of the function (its slope) is becoming less negative or more positive, hence increasing.
💡Concave Downwards
Concave downwards is a term used to describe a graph that curves in an upside-down U-shape, with both ends pointing downwards. In the video, this concept is used to illustrate a function whose slope is decreasing throughout its domain. For instance, a graph that consistently curves downwards, resembling an upside-down U, indicates that the function's rate of change (slope) is becoming less positive or more negative, hence decreasing.
💡Inflection Points
An inflection point is a specific point on a graph where the concavity of the function changes, transitioning from concave upwards to concave downwards or vice versa. The video emphasizes the importance of inflection points in understanding the behavior of a function, as they represent a change in the rate of change of the function's slope. For example, the video describes a scenario where a function starts with a decreasing slope (concave downwards), reaches a point where the slope is zero (the inflection point), and then the slope begins to increase (concave upwards).
💡Slope
Slope refers to the rate of change or steepness of a graph at a particular point. In the video, the concept of slope is central to understanding the concavity of a function. The video explains that the slope's behavior (increasing or decreasing) directly relates to whether the graph is concave upwards or downwards. For instance, a positive and increasing slope corresponds to a concave upwards graph, while a positive decreasing slope indicates a concave downwards graph.
💡Tangent Line
A tangent line is a straight line that touches a graph at a single point and has the same slope as the graph at that point. In the video, the tangent line is used to visualize the slope of the function at various points. The video describes how the slope of the tangent line changes as one moves along the graph, which helps to determine whether the function is concave upwards or concave downwards. The tangent line is a fundamental concept in calculus for analyzing the behavior of functions.
💡Derivative
The derivative is a mathematical concept that represents the rate of change of a function with respect to its input variable. In the video, the first derivative is associated with the slope of the function's graph. The video explains that understanding the derivative is crucial for analyzing the concavity of a function and identifying inflection points, as the second derivative provides information about the rate of change of the slope.
💡Second Derivative
The second derivative is the derivative of the first derivative, which measures the rate of change of the slope of a function. In the context of the video, the second derivative is used to determine the concavity of a function and to identify inflection points. If the second derivative is positive, the function is concave upwards, and if it is negative, the function is concave downwards. The video also explains that an inflection point occurs when the second derivative crosses zero, indicating a change in the concavity.
💡Rate of Change
Rate of change refers to how quickly a quantity changes with respect to another quantity. In the video, this concept is applied to the slope of a function, where the rate of change of the slope is described by the second derivative. The video emphasizes that understanding the rate of change is essential for determining whether a function's graph is concave upwards or concave downwards, as well as for identifying inflection points where the rate of change switches from increasing to decreasing or vice versa.
💡Visual Recognition
Visual recognition in the context of the video refers to the ability to identify the concavity of a function's graph by simply looking at it. The video provides strategies for visually recognizing concave upwards and concave downwards graphs, such as looking for the U or upside-down U shape. This skill is important for quickly understanding the behavior of a function without performing calculations, which is particularly useful in visualizing complex mathematical relationships.
💡Switching Signs
Switching signs refers to the change in the sign (positive or negative) of a mathematical quantity. In the video, this term is used to describe the change in the second derivative at an inflection point, where the rate of change of the slope changes from positive to negative or from negative to positive. The video explains that this sign change is a key characteristic of inflection points and is essential for determining the concavity transition on a function's graph.
Highlights

The concept of concavity is frequently encountered in calculus.

Concave upwards is visualized as a U shape.

Concave downwards is like an upside-down U shape.

Inflection points are transition points between concave upwards and downwards or vice versa.

The slope of a concave upwards function increases throughout its domain.

The slope of a concave downwards function decreases throughout its domain.

At an inflection point, the concavity of a function changes from concave downwards to upwards or vice versa.

The second derivative can be thought of as the derivative of the first derivative, representing the rate of change of the slope.

A positive second derivative indicates a concave upwards function, where the slope is increasing.

A negative second derivative indicates a concave downwards function, where the slope is decreasing.

At an inflection point, the second derivative must be equal to zero as the rate of change of the slope switches signs.

An inflection point is identified when the second derivative changes from positive to negative or from negative to positive.

The function's concavity and inflection points are crucial for understanding the behavior of the function's slope.

Visualizing the concavity and inflection points helps in understanding the function's overall shape and its derivatives.

The rate of change of the slope (first derivative) and its change (second derivative) provide insights into the function's dynamics.

The study of concavity and inflection points is essential in calculus for analyzing functions' behaviors.

Transcripts

Browse More Related Video

MATH1325 Lecture 10 2 - Concavity & Points of Inflection

Calculus 1: Concavity Examples

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Calculus AB/BC – 5.6 Determining Concavity of Functions over Their Domains

Concavity, Inflection Points, and Second Derivative

BusCalc 20 Concavity and Inflection Points

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus ConceptsConcavity ExplainedInflection PointsSlope AnalysisGraph InterpretationMathematical VisualizationDerivative ImplicationsEducational ContentMath TutorialAdvanced Math