Extreme derivative word problem (advanced) | Differential Calculus | Khan Academy
TLDRThe video script discusses a complex mathematical problem involving a parabola and normal lines. The focus is on finding the equation of the extreme normal line, which intersects the parabola at a point of maximum intersection in the second quadrant. The problem is solved using derivatives and quadratic equations, leading to the identification of the x-coordinate of the extreme normal line and its corresponding equation.
Takeaways
- 📈 The problem involves a parabola y = x^2 and normal lines intersecting it in the first quadrant.
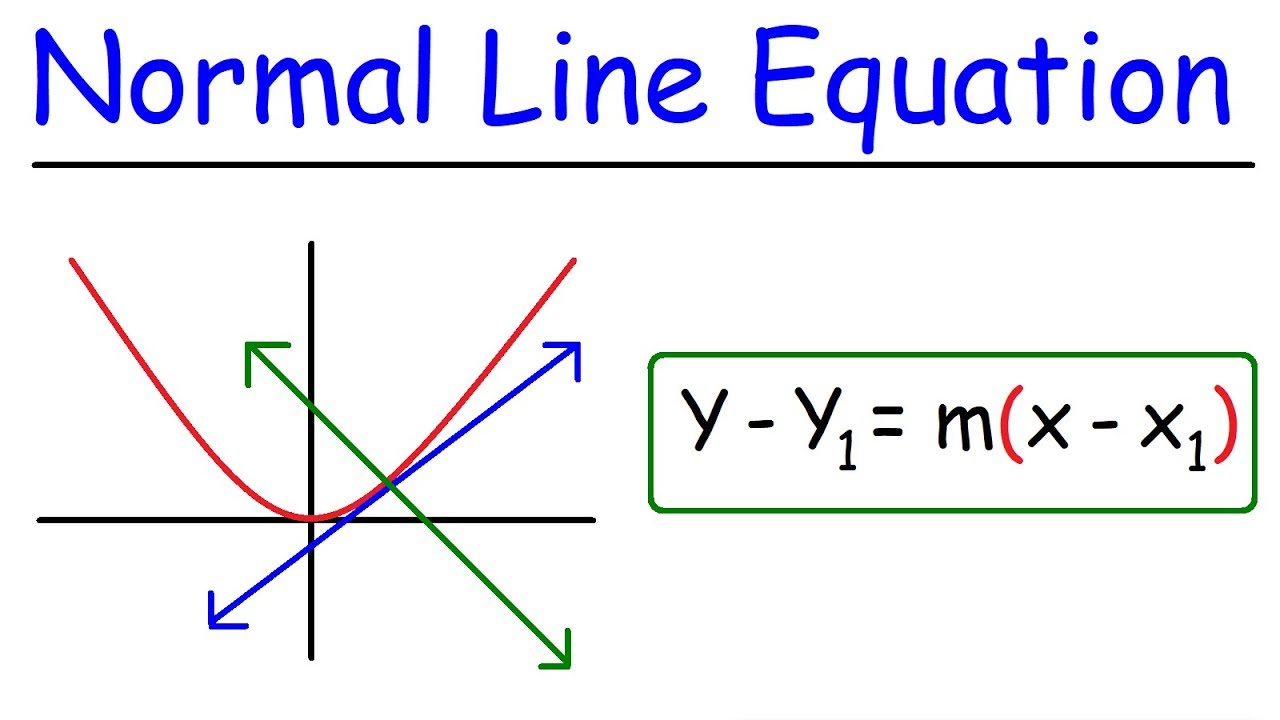
- 📌 Normal lines are defined as lines intersecting the parabola in such a way that their first quadrant intersection with the parabola is perpendicular.
- 🔍 The script describes a scenario where the x-coordinate of the second quadrant intersection of the normal line changes as the x-coordinate of the first quadrant intersection decreases.
- 📉 The second quadrant intersection's x-coordinate becomes less negative (absolute value decreases) as the first quadrant intersection's x-coordinate decreases.
- 🏁 An extreme normal line is identified where the second quadrant intersection reaches its smallest (most positive) value before normal lines start intersecting further away in the second quadrant.
- 🧮 The problem asks for the equation of the extreme normal line, which can be found using derivatives and the point-slope form of a line's equation.
- 🔧 The slope of the tangent line at any point on the parabola y = x^2 is found by taking the derivative, resulting in a slope of 2x.
- ⊥ The slope of the normal line is the negative inverse of the tangent line's slope, which is -1/(2x) at point x0.
- 📑 The equation of the normal line is derived using the point-slope form and is later set equal to the parabola's equation to find the points of intersection.
- 🔢 The x-values for the points of intersection are found by solving a quadratic equation, which yields two solutions corresponding to the first and second quadrant intersections.
- 🥇 The extreme normal line's equation is determined by substituting the x0 value that yields the maximum second quadrant intersection into the normal line's equation, resulting in y = -√2/2x + 1.
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is the analysis of a mathematical problem involving a parabola and normal lines.
What is the equation of the parabola mentioned in the transcript?
-The equation of the parabola mentioned in the transcript is y = x^2.
What does the term 'normal line' refer to in this context?
-In this context, a 'normal line' refers to a line that is perpendicular to the parabola at its first quadrant intersection point.
How many normal lines are shown in the figure according to the transcript?
-According to the transcript, there are 5 normal lines shown in the figure.
What happens to the x-coordinate of the second quadrant intersection as the x-coordinate of the first quadrant intersection gets smaller?
-As the x-coordinate of the first quadrant intersection gets smaller, the x-coordinate of the second quadrant intersection becomes less negative, which means it is moving towards zero.
What is the extreme normal line in the context of the problem?
-The extreme normal line is the line that represents the smallest negative value (or the highest absolute value) of the second quadrant intersection point.
What is the slope of the tangent line at any point on the parabola?
-The slope of the tangent line at any point on the parabola y = x^2 is given by the derivative of y with respect to x, which is 2x.
How is the slope of the normal line related to the slope of the tangent line?
-The slope of the normal line is the negative inverse of the slope of the tangent line. If the tangent line's slope is 2x, then the normal line's slope is -1/(2x).
What is the equation of the normal line in point-slope form?
-The equation of the normal line in point-slope form is y - y0 = m(x - x0), where m is the slope of the line and (x0, y0) is a point on the line.
How does the speaker determine the x0 value for the extreme normal line?
-The speaker determines the x0 value for the extreme normal line by setting the derivative of the second quadrant intersection with respect to x0 equal to zero and solving for x0, which results in x0 = 1/√2.
What is the equation of the extreme normal line?
-The equation of the extreme normal line is y = -√2/2x + 1/2, derived by substituting x0 = 1/√2 into the general equation of the normal line.
How does the speaker ensure clarity while solving the problem?
-The speaker ensures clarity by breaking down the problem into smaller parts, explaining each step thoroughly, and using visual aids (like the figure) to illustrate the concepts.
Outlines
📚 Introduction to the Complex Problem
The speaker introduces a challenging mathematical problem involving a parabola and normal lines. The problem is described as being more difficult than typical textbook exercises, and the speaker aims to work through it to enhance understanding. The problem involves a parabola defined by y=x^2 and the concept of a normal line, which is a line perpendicular to the parabola at its first quadrant intersection. The speaker sets the stage for the problem by discussing the behavior of normal lines and their intersections with the parabola in both the first and second quadrants.
📈 Deriving the Equation of Normal Lines
The speaker delves into the process of finding the equation of a normal line to the parabola y=x^2. By using derivatives, the speaker calculates the slope of the tangent line to the parabola at any point x, which is 2x, and subsequently determines the slope of the normal line, which is the negative reciprocal of the tangent's slope, resulting in -1/(2x). The speaker then applies the point-slope form of a line's equation to derive the equation of the normal line, highlighting the relationship between the x-values of the first and second quadrant intersections of the normal line with the parabola.
🔢 Solving for Intersection Points
The speaker continues by setting up and solving a quadratic equation to find the x-values where the normal line intersects the parabola. The process involves rearranging the equation, applying the quadratic formula, and simplifying the resulting expression. The speaker finds that the intersection points are given by the formula -1/(4x0) ± 1/(2√(x0^2 + 1/4)), which represents the x-coordinates in both the first and second quadrants. The speaker emphasizes the importance of understanding the behavior of these intersection points as the x-coordinate of the first quadrant intersection changes.
📉 Analyzing the Extreme Normal Line
The speaker focuses on identifying the extreme normal line, which corresponds to the maximum (or least negative) x-coordinate in the second quadrant intersection. By considering the second quadrant intersection as a function of the first quadrant x-coordinate, the speaker uses calculus to find the derivative and set it equal to zero to find the critical point. The speaker solves this equation to find the value of x0 that yields the extreme normal line, which is 1/√2. The speaker then substitutes this value back into the equation of the normal line to find the equation of the extreme normal line.
🏁 Conclusion and Final Equation
The speaker concludes the problem-solving process by summarizing the findings. The extreme normal line's equation is derived as y = -√2/2x + 1/2, which represents the line that achieves the maximum second quadrant intersection with the parabola y=x^2. The speaker reflects on the complexity of the problem and the steps taken to reach the solution, providing a clear and comprehensive understanding of the mathematical concepts and procedures involved.
Mindmap
Keywords
💡Parabola
💡Normal Line
💡First Quadrant
💡Second Quadrant
💡Tangent Line
💡Derivative
💡Slope
💡Intersection
💡Extreme Normal Line
💡Point-Slope Form
💡Quadratic Equation
Highlights
The problem involves a parabola y = x^2 and normal lines in the first quadrant.
A normal line is defined as one perpendicular to the parabola at its first quadrant intersection.
Five normal lines are shown in the figure, all appearing perpendicular to the parabola.
As the x-coordinate of the first quadrant intersection decreases, the second quadrant intersection's x-coordinate becomes less negative.
The problem discusses the behavior of normal lines as the x-coordinate of the first quadrant intersection changes.
The extreme normal line is identified as the bold line in the figure.
Once the normal line passes the extreme normal line, the x-coordinates of the second quadrant intersections of the parabola start to increase (become larger negative numbers).
The problem asks to find the equation of the extreme normal line.
The slope of the tangent line at any point on the parabola y = x^2 is found using derivatives, which is 2x.
The slope of the normal line is the negative inverse of the tangent line's slope, which is -1/(2x0).
The equation of the normal line is derived using the point-slope form and the point on the parabola.
The intersection points of the normal line and the parabola are found by setting the two equations equal to each other and solving the resulting quadratic equation.
The x-coordinates of the intersection points in the first and second quadrants are expressed in terms of x0.
The second quadrant intersection's x-coordinate is a function of the first quadrant x0, and its maximum value is sought.
The derivative of the second quadrant intersection with respect to x0 is taken to find the maximum point.
The x0 value that gives the extreme normal line is found by setting the derivative equal to zero and solving for x0.
The equation of the extreme normal line is found by substituting the x0 value that gives the maximum second quadrant intersection into the normal line equation.
The problem is solved by applying mathematical concepts such as derivatives, point-slope form, and quadratic equations.
The process demonstrates a deep understanding of mathematical problem-solving and the application of algebraic techniques.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: