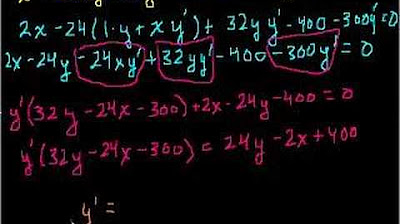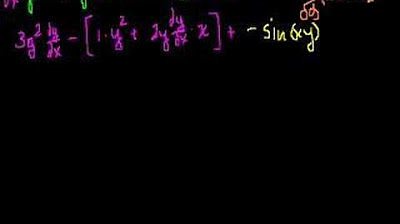Trig Implicit Differentiation Example

Khan Academy
13 Oct 200912:07
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a detailed walkthrough on implicitly differentiating the equation tan(x/y) = x+y, a common challenge for first-year calculus students. The presenter restructures the equation, applies the chain rule systematically, and simplifies the expressions to isolate dy/dx. The explanation emphasizes the chain rule's application in implicit differentiation, transforming a complex problem into a solvable algebraic one, ultimately providing the derivative dy/dx.

Takeaways
  • 📚 Implicit differentiation can be challenging for first-year calculus students, but practice with multiple examples helps.
  • 🔄 The process involves applying the derivative with respect to x to both sides of the given equation.
  • 💡 The derivative of the left side (tangent of b) requires recognizing that a is equivalent to the tangent of b, simplifying the differentiation process.
  • 📈 The derivative of the right side (x plus y) is straightforward, yielding 1 + (dy/dx).
  • 🌀 The chain rule is crucial for differentiating composite functions, and it naturally applies to implicit differentiation problems.
  • 📌 The derivative of a with respect to b is 1/cos^2(b), which is a standard trigonometric derivative.
  • 🔢 For the derivative of b with respect to x, rewrite b as x*y^(-1) and apply the product rule to find dy/dx.
  • 🔄 When differentiating 1 over y with respect to x, use the chain rule again and treat c as 1 over y to find the derivative.
  • 🧩 Solving for dy/dx involves algebraic manipulation, including factoring and dividing terms to isolate dy/dx.
  • 🎯 The final step is to divide both sides of the equation by the expression involving dy/dx to solve for it explicitly.
  • 📝 The key to implicit differentiation is understanding the chain rule and applying it step by step to simplify and solve for the unknown derivative.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is the process of implicitly differentiating the equation tan(y/x) = x + y, which is a common challenge for first-year calculus students.

  • What is the first step in implicitly differentiating the given equation?

    -The first step in implicitly differentiating the given equation is to apply the derivative with respect to x operator to both sides of the equation.

  • What is the derivative of the right side of the equation with respect to x?

    -The derivative of the right side of the equation (x + y) with respect to x is 1, since the derivative of x with respect to x is 1 and the derivative of y with respect to x is treated as an unknown, which we will solve for.

  • How is the left side of the equation rewritten to simplify the differentiation process?

    -The left side of the equation is rewritten by letting a = tan(b) and b = y/x, which allows the differentiation process to focus on the relationship between a and b, and then apply the chain rule to find the derivative of a with respect to x.

  • What is the chain rule and how is it applied in this context?

    -The chain rule states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In this context, it is used to find the derivative of a (tan(b)) with respect to x by first finding the derivative of a with respect to b, and then multiplying by the derivative of b with respect to x.

  • What is the derivative of tan(b) with respect to b?

    -The derivative of tan(b) with respect to b is 1 / (cos(b)^2) or 1 / (cosine squared of b).

  • How is the derivative of b = x * y^(-1) found?

    -The derivative of b with respect to x is found using the chain rule and the product rule. It results in 1 * y^(-1) + (derivative of y with respect to x) * (-1 * x) * y^(-1).

  • What is the role of the variable c in the script?

    -Variable c is introduced as 1/y to simplify the differentiation process of 1/y with respect to x. The derivative of c with respect to x is used to find the relationship between dy/dx and the given variables.

  • How is the final equation for dy/dx derived?

    -The final equation for dy/dx is derived by applying the chain rule multiple times, simplifying the expressions, and then solving for dy/dx by separating the terms involving dy/dx from those that do not.

  • What is the final form of the implicitly differentiated equation?

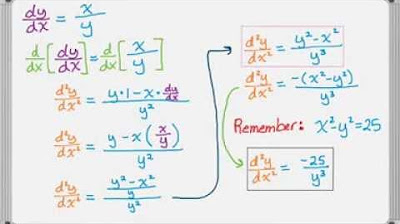
    -The final form of the implicitly differentiated equation is (1 / y) - (cosine squared of x / y) times (dy/dx) equals (1 + dy/dx), which is solved for dy/dx by dividing both sides by the expression (x / y^2 + cosine squared of x / y).

  • What is the key takeaway from the video script for solving implicit differentiation problems?

    -The key takeaway is that implicit differentiation problems can be solved by applying the chain rule and product rule systematically, and that with practice, the process becomes more intuitive and can be done efficiently.

Outlines
00:00
📚 Introduction to Implicit Differentiation

The video begins with the presenter discussing the concept of implicit differentiation, emphasizing its importance in calculus, especially for first-year students. The focus is on the equation tangent of x over y equals x plus y, and the presenter explains that the process involves applying the derivative with respect to x to both sides of the equation. The left side of the equation presents a bit of a challenge, but the right side is straightforward. The presenter introduces a method to simplify the process by rewriting the equation and applying the chain rule, which is a fundamental concept in calculus. The goal is to illustrate that implicit differentiation is not a new or complex concept but rather an application of the chain rule.

05:01
🔍 Derivative of Tangent and Application of Chain Rule

In this paragraph, the presenter delves deeper into the derivative of the tangent function and the application of the chain rule. The derivative of the right side of the equation is calculated to be 1, while the left side requires the use of the chain rule. The presenter explains that the derivative of a with respect to b, where a is the tangent of b, and b is x over y, is 1 over the cosine squared of b. The derivative of b with respect to x is then calculated using the product rule, resulting in an expression involving y to the power of negative one and x. The presenter emphasizes the importance of understanding the chain rule and how it naturally leads to the solution of implicit differentiation problems, rather than memorizing a separate set of rules.

10:05
🧠 Solving for dy/dx and Finalizing the Implicit Differentiation

The final paragraph focuses on solving for dy/dx, the derivative of y with respect to x. The presenter uses algebraic manipulation to isolate the dy/dx term, applying the chain rule to the derivative of 1 over y with respect to x. The process involves several steps, including multiplying both sides of the equation by the denominator and subtracting terms to isolate dy/dx on one side. The presenter then factors out dy/dx from the right side of the equation and divides both sides by the resulting expression to solve for dy/dx. The explanation is detailed, walking through each step of the algebraic process and emphasizing the application of the chain rule throughout the solution. The video concludes with the presenter expressing hope that the detailed walkthrough of the implicit differentiation process is helpful to the viewers, encouraging them to practice and become comfortable with the method.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used in calculus to find the derivative of a function when the function is not explicitly given in the form y = f(x). In the video, the process is applied to the equation tangent of x over y equals x plus y, where the goal is to find the derivative dy/dx without solving for y as a function of x first. This technique is crucial for first-year calculus students and is demonstrated step by step in the video to clarify its application and significance.
💡Derivative
In calculus, a derivative represents the rate of change of a function with respect to its independent variable. It is a fundamental concept used to analyze the behavior of functions, such as their slopes, critical points, and maxima/minima. In the context of the video, the derivative is used to find the rate of change of y with respect to x (dy/dx), which is the main objective of the implicit differentiation process.
💡Chain Rule
The chain rule is a fundamental rule in calculus that is used to find the derivative of a composite function. It states that the derivative of a function that is made up of other functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is applied multiple times to differentiate the implicit equation, helping to express the derivative of the tangent function and the x/y ratio in terms of x and y.
💡Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, are mathematical functions that relate angles to real numbers. They are widely used in various fields, including geometry, physics, and engineering. In the video, the tangent function is central to the equation being differentiated, and the derivative of the tangent function is one of the key components in solving for dy/dx.
💡Algebra
Algebra is a branch of mathematics that uses symbols and rules to solve equations and manipulate expressions. In the video, algebraic techniques are employed after the differentiation process to isolate and solve for dy/dx, demonstrating the interplay between calculus and algebra in solving mathematical problems.
💡Rate of Change
The rate of change is a concept in calculus that describes how a quantity changes in relation to another quantity. It is the core idea behind derivatives, which measure the rate of change of a function at a specific point. In the video, the rate of change is discussed in the context of finding the derivative of y with respect to x, which represents how y changes as x changes.
💡Sine and Cosine
Sine and cosine are two of the six trigonometric functions that are used to model periodic phenomena. They are based on the ratio of the sides of a right triangle and are essential in the study of triangles and waves. In the video, the derivative of the tangent function is expressed in terms of sine and cosine, specifically as 1 over cosine squared of the angle, highlighting the relationship between trigonometric functions and their derivatives.
💡Product Rule
The product rule is a calculus formula used to find the derivative of a product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, the product rule is applied when differentiating the expression x times y to the negative 1, which is part of the process to find dy/dx.
💡Critical Points
Critical points are points on the graph of a function where the derivative is either zero or undefined. They are important in calculus because they often represent maximum or minimum values of the function or points of inflection. Although not explicitly discussed in the video, understanding the derivative is a prerequisite for finding critical points, which is a common application of differentiation in calculus problems.
💡Limits
Limits are a fundamental concept in calculus that describe the behavior of a function as the input (or argument) approaches a certain value. They are used to define derivatives, integrals, and to understand the behavior of functions at points where the function may not be defined or where the derivative is not immediately clear. In the context of the video, while limits are not directly discussed, understanding them is crucial for a deeper comprehension of derivatives and their applications.
💡Functions
A function is a mathematical relationship between two variables where each value of the independent variable (usually denoted x) determines a unique value of the dependent variable (usually denoted y). Functions are central to the study of calculus, which explores their properties, such as continuity, differentiability, and integrability. In the video, the focus is on differentiating a function implicitly, meaning finding the rate of change of y with respect to x without explicitly solving for y as a function of x.
Highlights

The main topic discussed is implicit differentiation, specifically focusing on the equation tan(x/y) = x + y.

Implicit differentiation is a common challenge for first-year calculus students.

The process involves applying the derivative with respect to x operator to both sides of the equation.

The derivative of the right side of the equation is straightforward, while the left side requires more attention.

The video provides an example of rewriting the equation to facilitate the differentiation process, using a and b as substitutes for tan(b) and b = x/y respectively.

The chain rule is fundamental to solving this problem and is emphasized throughout the explanation.

The derivative of tan(b) with respect to x is found using the chain rule, which leads to the derivative of a with respect to b times the derivative of b with respect to x.

The derivative of b with respect to x is calculated using the product rule, resulting in a complex expression.

The derivative of 1/y with respect to x is determined by applying the chain rule again, leading to a further breakdown of the expression.

The process simplifies the complex derivative expression by combining like terms and applying algebraic techniques.

The final step is to solve for dy/dx, which is the main goal of the implicit differentiation.

The video emphasizes that implicit differentiation problems can be approached using the chain rule and algebraic techniques, rather than memorizing specific rules.

The example provided is a comprehensive walkthrough of implicit differentiation, demonstrating the application of the chain rule at every step.

The video aims to demystify implicit differentiation by showing that it is a natural application of the chain rule and algebra, rather than a separate, complex topic.

The transcript provides a detailed explanation of the steps involved in implicit differentiation, making it a valuable resource for students and educators.

The video concludes with a summary of the process, emphasizing the transition from complex derivative expressions to a solvable algebraic equation for dy/dx.

Transcripts

Browse More Related Video

Implicit Differentiation for Calculus - More Examples, #1

Second Derivative of Implicit Function

Implicit Differentiation

More implicit differentiation

Second derivatives (implicit equations): find expression | AP Calculus AB | Khan Academy

Implicit Differentiation (part 2)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus TutorialImplicit DifferentiationTrigonometric FunctionsChain RuleMathematics EducationFirst Year CalculusAlgebraic Problem SolvingTrig DerivativesOnline LearningEducational Content