Law of Sines - Basic Introduction

The Organic Chemistry Tutor
2 Jul 202012:33
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video offers a concise introduction to the Law of Sines, a fundamental formula used to solve for unknown sides and angles in triangles. The presenter demonstrates how to apply the formula by working through two examples, one with known angles and another with known sides. The video guides viewers through the process of calculating angles and sides, emphasizing the importance of checking the sum of angles to ensure a valid triangle. It also highlights the relationship between larger angles and longer sides, providing a quick validation technique for the calculated results. The video concludes with a cautionary note on the potential for two possible solutions when using the Law of Sines, illustrating how to determine the correct triangle configuration.

Takeaways
  • 📚 The Law of Sines is a mathematical formula used to solve triangles.
  • 📐 The formula is expressed as sin(A)/a = sin(B)/b = sin(C)/c, where capital letters represent angles and lowercase letters represent sides.
  • 🔍 To find an unknown angle in a triangle, subtract the known angles from 180 degrees.
  • 🧐 When using the Law of Sines, ensure your calculator is in degree mode to avoid incorrect calculations.
  • 🔢 Cross-multiply when solving for an unknown side using the Law of Sines formula.
  • 📉 After calculating a side, divide both sides by the sine of the known angle to isolate the variable.
  • 📏 The longest side should be opposite the largest angle, and the shortest side opposite the smallest angle.
  • 🔄 When given two angles and a side, you can find the third angle and then the remaining sides.
  • ⚠️ Be aware that the inverse sine function can yield two possible angles, and both should be tested for triangle validity.
  • 📝 For problems with two sides and an angle given, use the Law of Sines to find the missing angle and then the other sides.
  • 📉 When solving for side lengths, use the exact values for calculations to ensure accuracy, especially when dealing with rounded values.
Q & A

  • What is the Law of Sines used for?

    -The Law of Sines is used to solve triangles, particularly when you know some angles and sides and need to find the missing ones.

  • What is the formula for the Law of Sines?

    -The formula for the Law of Sines is \( \frac{\sin(\angle A)}{\text{side A}} = \frac{\sin(\angle B)}{\text{side B}} = \frac{\sin(\angle C)}{\text{side C}} \), where the capital letters represent the angles and the lowercase letters represent the sides of the triangle.

  • How can you find angle C if you know the other two angles in a triangle?

    -You can find angle C by subtracting the sum of the other two angles from 180 degrees, since the sum of all angles in a triangle is always 180 degrees.

  • How do you calculate side b if you know angle a, side a, and angle b?

    -You can calculate side b by using the Law of Sines formula, cross-multiplying, and then isolating side b by dividing both sides of the equation by \( \sin(\angle a) \).

  • What is the value of side b in the example where angle a is 53 degrees, side a is 8, and angle b is 62 degrees?

    -In the example, side b is calculated to be 8.84 by cross-multiplying and dividing \( 8 \times \sin(62) \) by \( \sin(53) \).

  • How do you calculate side c if you know angle a, side a, and angle c?

    -Similar to calculating side b, you use the Law of Sines formula, cross-multiply, and then isolate side c by dividing both sides of the equation by \( \sin(\angle a) \).

  • What is the value of side c in the example where angle a is 53 degrees, side a is 8, and angle c is 65 degrees?

    -In the example, side c is calculated to be 9.08 by cross-multiplying and dividing \( 8 \times \sin(65) \) by \( \sin(53) \).

  • How can you check if your answers for the sides of a triangle make sense?

    -You can check your answers by ensuring that the sides opposite larger angles are longer than those opposite smaller angles, as the size of the angle is directly related to the length of the side opposite it.

  • What is the first step when you are given two sides and one angle in a triangle and need to find the other elements?

    -The first step is to calculate one of the missing angles using the Law of Sines formula and the known angle and sides.

  • Why is it important to use the inverse sine function in certain triangle problems?

    -The inverse sine function is used to find the measure of an angle when you have the ratio of the opposite side to the hypotenuse, which is often the case in triangle problems involving the Law of Sines.

  • What is the significance of considering the complementary angle when using the inverse sine function?

    -The significance lies in the fact that the sine of an angle and its complementary angle (180 degrees minus the angle) are equal, which means you can get two possible angles for a given sine value, and both must be considered when solving the triangle.

  • How can you determine if a second triangle is possible when you have two possible angles for angle b?

    -You can determine if a second triangle is possible by checking if the sum of the angles in the triangle equals 180 degrees. If they do not exceed this sum, the second triangle is possible.

  • What is the process for calculating angle c and side c for both possible triangles?

    -For both possible triangles, you calculate angle c by subtracting the other two known angles from 180 degrees. Then, you calculate side c using the Law of Sines formula with the exact values for angle a and side a, and the calculated angle c.

  • How do you ensure the accuracy of your results when using rounded values in the Law of Sines calculations?

    -To ensure accuracy, it's best to use the exact values for angle a and side a when calculating side c, as rounded values for angle b can slightly affect the calculated value of side c.

Outlines
00:00
📚 Introduction to the Law of Sines

This paragraph introduces the Law of Sines, a mathematical formula used to solve triangles. The formula is given as the ratio of the sine of each angle to its opposite side, which are equal for all three angles and sides in a triangle. The video demonstrates how to calculate the third angle of a triangle, given two angles and one side, by using the fact that the sum of angles in a triangle is 180 degrees. It then proceeds to use the Law of Sines to find an unknown side (side b) when two angles and the other side (side a) are known. The process involves cross-multiplying and using the sine function in a calculator set to degree mode. The paragraph concludes with a practical tip to check the validity of the calculated sides and angles by ensuring that larger angles are opposite longer sides.

05:02
🔍 Solving Triangles with Two Sides and an Angle

This paragraph delves into solving a triangle when two sides and one non-included angle are known. The Law of Sines is applied to find the second angle (angle b). The process involves setting up the Law of Sines formula and cross-multiplying to isolate the sine of the unknown angle. The inverse sine function is then used to find the measure of angle b. The paragraph highlights the importance of considering both possible angles that could result from the sine calculation due to the periodic nature of the sine function. It demonstrates how to determine if both possible triangles are valid by checking if the sum of their angles equals 180 degrees. The video then solves for the third angle (angle c) and the unknown side (side c) for both possible triangles, emphasizing the use of exact values over rounded ones to ensure accuracy.

10:02
📐 Applying the Law of Sines to Find Side Lengths

The final paragraph focuses on calculating the unknown side lengths of two possible triangles using the Law of Sines. It explains the importance of using the exact values for angle a and side a to find side c, as these are less likely to introduce rounding errors. The formula is rearranged to solve for side c, and the process is demonstrated for both triangles, yielding different side lengths based on the different angle measurements. The paragraph reinforces the geometric principle that the largest angle is opposite the longest side and vice versa, which is used to validate the calculated side lengths. The video concludes by summarizing the steps and emphasizing the correct application of the Law of Sines to solve for unknown sides and angles in various types of triangles.

Mindmap
Keywords
💡Law of Sines
The Law of Sines is a mathematical formula used in trigonometry to solve triangles, particularly when the ratio of the length of a side to the sine of its opposite angle is constant. In the video, it is the central formula used to find unknown angles and sides of triangles. The script provides a step-by-step application of the Law of Sines to calculate missing elements of a triangle, demonstrating its practical use in solving various problems.
💡Triangle
A triangle is a polygon with three edges and three vertices. In the context of the video, the triangle serves as the geometric figure whose properties are being analyzed and calculated using the Law of Sines. The script discusses solving triangles with different given measurements, such as angles and sides, to find the missing elements.
💡Sine
Sine is a trigonometric function that relates the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right-angled triangle. In the video, sine is used in the Law of Sines formula to calculate angles and sides of non-right-angled triangles, as demonstrated in the examples provided.
💡Angle
An angle is a measure of rotation or the amount of turn between two lines or rays that intersect. In the video, angles are fundamental components of the triangles being solved. The script explains how to calculate unknown angles using the Law of Sines when other elements of the triangle are known.
💡Side
A side in the context of a triangle refers to one of the segments that connect the vertices. The video script uses the term 'side' to denote the lengths of these segments, which are calculated using the Law of Sines when the angles are known or vice versa.
💡Cross Multiply
Cross multiplying is a mathematical technique used to solve equations involving proportions. In the video, cross multiplying is utilized to isolate variables and solve for unknown sides or angles in the context of applying the Law of Sines.
💡Inverse Sine
The inverse sine, also known as arcsine, is the reverse operation of the sine function. It is used to find an angle when the sine value is known. In the video, the inverse sine function is applied to determine angles when the sine of an angle is calculated using the Law of Sines.
💡Complementary Angles
Complementary angles are two angles that add up to 90 degrees. In the video, the concept is extended to any two angles that sum to 180 degrees, which is necessary when considering the properties of a triangle. The script explains how to find a complementary angle to determine if a second possible triangle configuration is valid.
💡Radian Mode
Radian mode is a setting on calculators that allows for calculations in radians instead of degrees. The video script cautions viewers to ensure their calculators are in degree mode to avoid incorrect calculations when using the Law of Sines, as the sine values differ between radians and degrees.
💡Check Answers
Checking answers is a verification process to ensure that the calculated results make sense within the context of the problem. In the video, the script suggests a quick method to check answers by ensuring that the sides opposite larger angles are longer, which is consistent with the properties of triangles.
Highlights

Introduction to the Law of Sines and its formula.

Explanation of how the Law of Sines can be used to solve triangles.

The formula is sin(A)/a = sin(B)/b = sin(C)/c, where capital letters represent angles and lowercase represent sides.

Calculating angle C using the sum of angles in a triangle (180 degrees).

Method to calculate side b using the Law of Sines formula.

Cross-multiplying to isolate variable b and calculate its value.

Calculating side c using a similar approach as for side b.

Verification method to check if calculated sides correspond to angles correctly.

Starting a new problem with given two sides and one angle.

Using the Law of Sines to calculate angle b when two sides and one angle are known.

Cross-multiplying to find the sine of angle b.

Using the inverse sine function to calculate the measure of angle b.

Consideration of the possibility of two angles having the same sine value due to the sine function's periodicity.

Method to determine the second possible angle by subtracting from 180 degrees.

Drawing two triangles with both possible angle b values to check for possibility.

Calculating angle c for both triangles using the sum of angles in a triangle.

Solving for side c in both triangles using the Law of Sines formula.

Verification of the relationship between the largest angle and the longest side in a triangle.

Conclusion summarizing the use of the Law of Sines formula for solving triangles.

Transcripts

Browse More Related Video

How to Use the Law of Sines in Trigonometry (Precalculus - Trigonometry 32)

Law of Sines, Basic Introduction, AAS & SSA - One Solution, Two Solutions vs No Solution, Trigonomet

Law of Cosines, Finding Angles & Sides, SSS & SAS Triangles - Trigonometry

How To Calculate The Missing Angle In a Triangle

Trigonometry - How To Solve Right Triangles

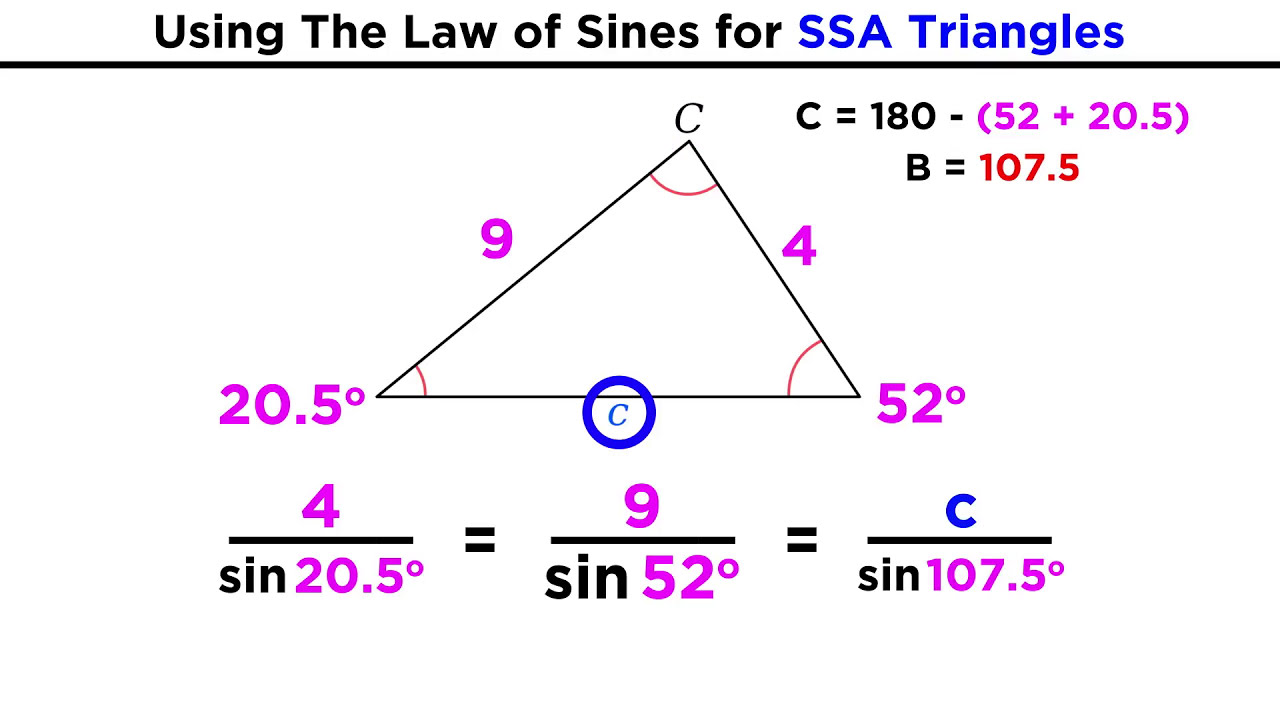
The Law of Sines

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Law of SinesTriangle SolvingMathematicsEducational VideoTrigonometryAngle CalculationSide LengthsFormula ApplicationGeometry ProblemsMath Tutorial