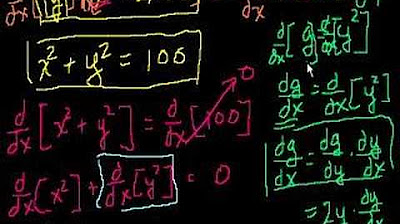Derivative of x^(x^x) | Taking derivatives | Differential Calculus | Khan Academy

Khan Academy
2 Oct 200909:02
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the process of solving complex implicit differentiation problems, using the natural logarithm to simplify expressions. It walks through a classic problem, y = x^x, and its derivative, then tackles a more complicated problem, y = x^(x^x), applying the product rule and chain rule. The solution involves taking the natural log of both sides and using previously derived results to find dy/dx, showcasing the elegance and complexity in mathematical operations.

Takeaways
  • 📚 The problem involves finding the derivative of y = x^x with respect to x.
  • 🔍 The approach to solving the problem is through implicit differentiation and the use of natural logarithms.
  • 🌟 The natural log method simplifies the equation by converting y = x^x to ln(y) = x*ln(x).
  • 📈 The derivative of the natural log form with respect to x is found using the chain rule and product rule.
  • 🤔 The derivative of ln(y) with respect to y is 1/y, and the derivative of ln(x) with respect to x is 1/x.
  • 🧠 The key to solving the problem is recognizing the relationship between the derivative of x^x and the natural log rules.
  • 🚀 The derivative of y with respect to x is given as dy/dx = y*(ln(x) + 1)/x.
  • 🌐 The script introduces a more complex problem, y = x^(x^x), which follows a similar solving process.
  • 🛠️ The derivative of the complex problem is calculated using the previously found derivative of x^x.
  • 📊 The final result for the complex problem is expressed as a combination of terms involving x, natural logs, and y.
  • 🎓 The script highlights the elegance and complexity that can be found in mathematical operations and derivatives.
Q & A

  • What is the main problem discussed in the script?

    -The main problem discussed is finding the derivative of y with respect to x for the function y = x^x.

  • How does the script suggest solving the main problem?

    -The script suggests solving the problem by taking the natural log of both sides of the equation and then applying the power and chain rules to find the derivative.

  • What is the significance of taking the natural log of both sides of the equation?

    -Taking the natural log simplifies the exponential function into a form that can be more easily differentiated using standard rules like the power rule and chain rule.

  • What is the derivative of y with respect to x for the function y = x^x?

    -The derivative of y with respect to x for the function y = x^x is dy/dx = x^x * (ln(x) + 1).

  • What is the more complex problem introduced after solving the main problem?

    -The more complex problem introduced is finding the derivative of y with respect to x for the function y = x^(x^x).

  • How does the script approach the more complex problem?

    -The script approaches the more complex problem by again taking the natural log of both sides and applying the rules of differentiation, using the previously found derivative of x^x.

  • What is the final expression for the derivative of y with respect to x for the function y = x^(x^x)?

    -The final expression for the derivative is dy/dx = y * (x^x * ln(x) + 1/x * x^(x-1)) where y = x^(x^x).

  • What is the importance of the chain rule in this context?

    -The chain rule is important for differentiating composite functions, which is the case when dealing with functions like y = x^x or y = x^(x^x) where the outer function is also an exponential function.

  • Why is it beneficial to solve the simpler problem first?

    -Solving the simpler problem first provides the foundational understanding and tools needed to tackle the more complex problem, such as the derivative of x^x, which is directly applicable to the complex problem.

  • How does the script illustrate the elegance of mathematics?

    -The script illustrates the elegance of mathematics by showing how complex problems can be broken down into simpler, manageable parts, and how seemingly complicated derivatives can result from simple and elegant operations.

  • What is the role of the product rule in differentiating the given functions?

    -The product rule is used to differentiate the functions when expressing the derivative of y with respect to x, as it helps in finding the derivative of the product of two functions, namely x^x and ln(x).

Outlines
00:00
📚 Solving Implicit Differentiation Problems

The paragraph introduces a classic implicit differentiation problem where the function y is expressed as y = x^x. The speaker explains that the challenge lies in the unconventional exponent, which doesn't fit the power rules directly. The solution involves taking the natural logarithm of both sides of the equation, which simplifies the expression to a form that allows the application of power and logarithm rules. The speaker then derives the derivative of y with respect to x, using the chain rule and product rule, and emphasizes the utility of this method for solving more complex problems later in the video.

05:01
🤔 Tackling a More Complex Implicit Differentiation

The speaker presents a more complex problem where y is defined as x^(x^x) and the task is to find the derivative dy/dx. The approach is similar to the previous problem, using natural logarithms to simplify the expression. However, the presence of nested exponents adds an extra layer of complexity. The speaker applies the chain rule and product rule, referencing a previously solved expression for the derivative of x^x. The final result is a complex expression that incorporates the natural logarithm of x, exponents, and a term involving 1/x. The speaker highlights the elegance of mathematics, where complex operations can sometimes yield surprisingly simple or intricate results.

Mindmap
Keywords
💡implicit differentiation
Implicit differentiation is a method used in calculus to find the derivative of a function when the relationship between the variables is not explicitly expressed as y = f(x). In the video, this technique is applied to complex equations where the dependent variable y is not isolated on one side, such as in the equation y = x^x. The process involves taking the natural logarithm of both sides to transform the equation into a form that allows for differentiation using standard rules.
💡natural logarithm
The natural logarithm, often denoted as ln, is the logarithm to the base e (where e is an irrational number approximately equal to 2.71828). It is a fundamental concept in calculus and is used to solve exponential equations. In the context of the video, taking the natural logarithm of both sides of an equation is a key step in simplifying complex exponential relationships and facilitating differentiation.
💡chain rule
The chain rule is a fundamental principle in calculus used to find the derivative of a composite function. It states that the derivative of a function composed of other functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is applied when differentiating the natural logarithm of y with respect to x, which involves differentiating the inner function (ln(y)) and then multiplying by the derivative of the outer function (1/y).
💡power rules
Power rules in calculus are used to find the derivative of functions with exponents. The basic power rule states that the derivative of x^n, where n is a constant, is n*x^(n-1). However, in the video, the power rule is not directly applicable as the exponent itself varies with x. Instead, the natural logarithm is used to handle the variable exponent before applying differentiation.
💡product rule
The product rule is a calculus formula used to find the derivative of a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, the product rule is applied when differentiating the expression that results from applying the chain rule to the natural logarithm of y.
💡exponential functions
Exponential functions are mathematical functions of the form f(x) = a^x, where a is a constant and x is the variable. These functions are crucial in many areas of mathematics and science, including growth and decay processes. In the video, the main challenge is to differentiate an exponential function where the exponent itself is a function of x, which is a more complex scenario than typical exponential functions.
💡derivative
In calculus, the derivative of a function represents the rate of change or the slope of the function at any given point. It is a fundamental concept used to analyze the behavior of functions, such as their increases, decreases, and inflection points. The video is centered around finding the derivatives of complex functions involving exponentials with variable bases.
💡variable exponent
A variable exponent is an exponent that changes with the variable, making the function more complex than a standard exponential function with a constant exponent. In the video, the challenge lies in differentiating functions where not only the base but also the exponent is a function of the variable x.
💡simplifying equations
Simplifying equations involves using mathematical techniques to reduce complex expressions to a more manageable form. In the context of the video, simplification is crucial before applying differentiation rules, as it allows for the application of standard calculus techniques to complex problems.
💡rates of change
Rates of change are a central concept in calculus that describe how a quantity changes in response to changes in another quantity. Derivatives are used to calculate rates of change and can provide insights into the behavior of functions, such as their instantaneous rate of change at a specific point. The video focuses on finding the rate of change (dy/dx) for complex exponential functions with variable exponents.
💡complex problems
Complex problems in mathematics are those that involve intricate relationships or higher levels of abstraction, often requiring advanced techniques for solution. In the video, complex problems refer to differential equations with variable exponents, which necessitate the use of natural logarithms, implicit differentiation, and other advanced calculus concepts.
Highlights

The problem presented involves implicit differentiation with the equation y = x^x.

The approach to solving this problem is to take the natural log of both sides of the equation.

After taking the natural log, the equation becomes simpler: ln(y) = x * ln(x).

The derivative of y with respect to x can be found by applying the chain rule and product rule.

The derivative of ln(y) with respect to y is 1/y, and the derivative of ln(x) with respect to x is 1/x.

The final expression for the derivative is dy/dx = y * (ln(x) + 1) / x.

An even more complex problem is introduced where y = x^(x^x).

The natural log is used again to simplify the complex exponent in the new problem.

The derivative of x^(x^x) with respect to x is found by applying the previously derived rule for x^x.

The final expression for the derivative of the complex problem is dy/dx = y * (x^x * ln(x) + 1/x * x^(x-1)).

The process demonstrates the power of logarithms and differentiation rules in solving complex problems.

The solution to the complex problem showcases the elegance and unexpected results that can come from mathematical operations.

The video emphasizes the importance of understanding and applying basic mathematical tools to tackle more difficult problems.

The problem-solving approach can be applied to a variety of mathematical challenges, not just those involving exponents.

The video serves as a tutorial on implicit differentiation and the application of natural logarithms.

The solution process is detailed, walking through each step to ensure clarity and understanding.

The video highlights the potential for elegant solutions even in the face of complex mathematical expressions.

The transcript provides a comprehensive guide to solving implicit differentiation problems involving exponents.

Transcripts

Browse More Related Video

The Derivative of ln(x) via Implicit Differentiation

Implicit Differentiation

Implicit Differentiation (part 2)

Logarithmic Differentiation | Example: x^sinx

Second derivatives (implicit equations): find expression | AP Calculus AB | Khan Academy

Implicit Differentiation Method

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsImplicit DifferentiationLogarithmsDerivativesProblem SolvingComplex ProblemsEducational ContentMath TutorialElegant SolutionsAdvanced Math