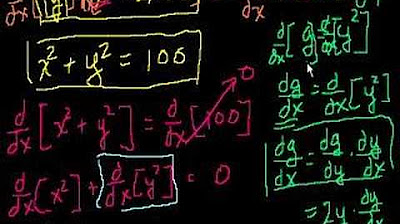More chain rule and implicit differentiation intuition
TLDRThe video script discusses the chain rule in calculus, aiming to improve the audience's intuition about it and its application to implicit differentiation. By using an example where 'a' is defined in terms of 'b', and 'b' in terms of 'c', the script illustrates how the chain rule can be applied to find the derivative of 'a' with respect to 'c'. The explanation is further solidified with another example of implicit differentiation, demonstrating how the chain rule can be used to differentiate expressions involving variables defined in terms of others. The video emphasizes understanding the underlying concepts rather than just memorizing formulas.
Takeaways
- 📚 The chain rule is essential for understanding how to differentiate composite functions and is key in both implicit and explicit differentiation.
- 🔄 The chain rule states that the derivative of a composite function is the derivative of the outer function with respect to the inner function times the derivative of the inner function with respect to the variable of interest.
- 🌟 Intuition can be developed for the chain rule by viewing it as multiplying two fractions where the denominator of one fraction is the numerator of the other, leading to cancellation and simplification.
- 📈 To find the derivative of 'a' with respect to 'c', given 'a = b^2' and 'b = sin(c)', you would apply the chain rule: da/dc = (da/db) * (db/dc).
- 👌 As an example, the derivative of 'a' with respect to 'c' in the given scenario is 2b*cos(c), and by substituting b with sin(c), the result is 2*sin(c)*cos(c).
- 🔄 Understanding the chain rule can also help in tackling implicit differentiation problems, where the relationship between variables is not explicitly given.
- 🧠 Variable substitution can help clarify the process of implicit differentiation. By defining new variables (e.g., a = y^2, b = x^3), the problem can be reformulated to apply the chain rule more intuitively.
- 📊 The product rule is also essential in differentiation. It states that the derivative of a product of two functions is the derivative of the first function times the second plus the first times the derivative of the second.
- 🌐 In the context of implicit differentiation, the chain rule allows us to differentiate expressions involving variables that are not explicitly defined in terms of the differentiation variable.
- 🎓 The process of implicit differentiation involves applying the chain rule to the components of a given expression, even when those components are not fully expressed in terms of the differentiation variable.
- 🚀 With practice and understanding of the chain rule, differentiation problems can be approached more directly and intuitively, leading to efficient problem-solving.
Q & A
What is the chain rule in calculus?
-The chain rule is a fundamental principle in calculus that is used to find the derivative of a composite function. It states that the derivative of a function that is composed of other functions is equal to the derivative of the outer function with respect to the inner function, multiplied by the derivative of the inner function.
How does the chain rule apply to the given example of a being dependent on b, and b on c?
-In the provided example, the chain rule is applied to find the derivative of 'a' with respect to 'c'. Here, 'a' is defined as 'b' squared, and 'b' is the sine of 'c'. The chain rule tells us that the derivative of 'a' with respect to 'c' is the product of the derivative of 'a' with respect to 'b' and the derivative of 'b' with respect to 'c', which is mathematically represented as (da/db) * (db/dc).
What is the derivative of a with respect to b?
-The derivative of 'a' with respect to 'b', given that 'a' is equal to 'b' squared, is 2b. This is because when differentiating the square of a function, you multiply the base by 2, following the power rule of differentiation.
What is the derivative of b with respect to c?
-The derivative of 'b' with respect to 'c', where 'b' is the sine of 'c', is the cosine of 'c'. This is based on the basic differentiation rule for trigonometric functions, where the derivative of the sine function is the cosine function.
How can we express the derivative of a with respect to c in terms of both b and c?
-By applying the chain rule, the derivative of 'a' with respect to 'c' can be expressed as (da/db) * (db/dc), which simplifies to 2b * cos(c), given that 'a' is 'b' squared and 'b' is the sine of 'c'.
What is the significance of understanding the chain rule in terms of fractions?
-Understanding the chain rule in terms of fractions helps to visualize the process as multiplying two fractions where the denominator of the first fraction is the same as the numerator of the second fraction. This simplification through cancellation of common terms provides an intuitive grasp of how the chain rule operates in practice.
How does the chain rule relate to differentials?
-The chain rule relates to differentials in that it describes the relationship between the infinitesimal changes in the variables involved. The numerator and denominator in the chain rule represent differentials, and their ratio gives the rate of change or the derivative of the function.
What is the product rule in calculus?
-The product rule is a differentiation rule in calculus that is used to find the derivative of a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function.
How can we apply the product rule to the expression y squared x to the third with respect to x?
-To apply the product rule to the expression y squared x to the third, we first define 'a' as y squared and 'b' as x to the third. The derivative with respect to x is then found by taking the derivative of 'a' times 'b' plus the derivative of 'b' times 'a'. The derivative of 'a' with respect to x is 2y times the derivative of y with respect to x, and the derivative of 'b' with respect to x is 3x squared.
What is implicit differentiation?
-Implicit differentiation is a method used to differentiate an equation where the relationship between the variables is not explicitly expressed as a function of one variable. It involves differentiating both sides of an equation with respect to a variable without explicitly solving for one variable in terms of the others.
How does the chain rule help in understanding implicit differentiation?
-The chain rule helps in understanding implicit differentiation by showing that it is essentially the application of the chain rule to equations that are not explicitly written as functions. It helps to break down the process into simpler steps of taking derivatives of both sides of an equation with respect to the variable of interest.
What is the final result of the derivative of y squared x to the third with respect to x?
-The final result of the derivative of y squared x to the third with respect to x is 2y * dy/dx + 3x^2 * y^2, where dy/dx represents the derivative of y with respect to x.
Outlines
📚 Intuition Behind the Chain Rule
This paragraph introduces the concept of the chain rule in calculus and aims to develop a better intuition for its application, particularly in implicit differentiation. It begins by setting up a scenario where 'a' is defined in terms of 'b', and 'b' in terms of 'c', and then poses the question of finding the derivative of 'a' with respect to 'c'. The explanation unfolds by illustrating the chain rule's process, which involves multiplying the derivative of 'a' with respect to 'b' by the derivative of 'b' with respect to 'c'. The paragraph simplifies the chain rule to the multiplication of fractions and emphasizes the intuitive aspect of the rule, which is about dealing with infinitesimal changes in variables. The paragraph concludes by calculating the derivatives and applying the chain rule to find the derivative of 'a' with respect to 'c', and then further clarifies the concept by substituting 'b' back into the equation to express 'a' directly in terms of 'c'.
🔄 Applying the Chain Rule to Implicit Differentiation
The second paragraph delves into the application of the chain rule in implicit differentiation problems. It starts by setting up a new scenario involving 'y' squared and 'x' to the third. The paragraph explains how to apply the product rule to find the derivative with respect to 'x' of the given expression. It then transitions into explaining the chain rule's role in this context, highlighting how to deal with 'a' defined in terms of 'y' and 'b' defined in terms of 'x'. The explanation includes the cancellation of terms and the process of finding the derivatives of 'a' and 'b' with respect to 'x'. The paragraph concludes by emphasizing the intuitive understanding of implicit differentiation as essentially applying the chain rule and encourages viewers to apply this understanding to similar problems.
🙏 Seeking Feedback and Closing Remarks
In the final paragraph, the speaker seeks feedback from the viewers and encourages them to request more videos on the topic if they found this one helpful. The speaker reflects on the content covered in the video, hoping to have clarified the concepts of the chain rule and its application in implicit differentiation. The paragraph ends with a brief farewell, indicating the video's conclusion and expressing a desire to see the viewers again in future content.
Mindmap
Keywords
💡Chain Rule
💡Implicit Differentiation
💡Derivative
💡Product Rule
💡Variable Substitution
💡Rate of Change
💡Intuition
💡Fractions
💡Differentials
💡Sine and Cosine Functions
💡Explicit and Implicit Functions
Highlights
Exploring the chain rule to develop a better intuition for implicit differentiation and vice versa.
Using variables a, b, and c to generalize the concept of derivatives and avoid confusion with specific functions like f(x).
The derivative of a with respect to c is found by multiplying the derivative of a with respect to b by the derivative of b with respect to c.
The chain rule is a simple concept of multiplying two fractions where the denominator of one fraction is the numerator of the next.
The derivative of a with respect to b is 2b, demonstrating how to calculate the change of a variable based on another.
The derivative of b with respect to c is the cosine of c, showing the relationship between trigonometric functions in differentiation.
Substituting b with sine of c to express the derivative of a with respect to c in terms of c alone.
Rewriting the chain rule problem with a defined in terms of c to provide a more traditional approach to understanding the chain rule.
Applying the chain rule to find the derivative of sine of c squared with respect to c.
Explaining the product rule as the derivative of a times b is the derivative of a times b plus the derivative of b times a.
Using variable substitution to define a as y squared and b as x to the third for an implicit differentiation problem.
The derivative of a with respect to x involves the chain rule, taking the derivative of a with respect to y and then the derivative of y with respect to x.
The derivative of b with respect to x is 3x squared, as b is explicitly defined in terms of x.
The final answer for the derivative of y squared x to the third with respect to x is 2y dy/dx times (x to the third + 3x squared y squared).
Implicit differentiation is essentially applying the chain rule, as demonstrated through the problem-solving process.
The video aims to provide intuition for chain rule and implicit differentiation, making complex concepts more accessible.
The presenter encourages feedback for more videos on the topic, showing an openness to educational collaboration.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: