Maxima Minima Slope Intuition

Khan Academy

11 Jun 200809:37

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the fundamental concepts of concavity, maxima, minima, and inflection points in calculus, typically introduced in the first semester. It emphasizes the importance of understanding the underlying intuition rather than just memorizing rules for exams. The speaker explains how the first derivative being zero indicates interesting points on a curve and how the sign of the second derivative relates to the concavity of the function. The goal is to provide a deeper understanding that will be remembered beyond the classroom.

Takeaways

📚 The video discusses key concepts in calculus such as concavity, maxima, minima, and inflection points.
🧠 The importance of understanding the intuition behind calculus concepts rather than just memorizing rules is emphasized.
📈 The video introduces the concept of 'interesting points' on curves where the slope is equal to zero.
🔍 The local maximum and minimum points on a curve are identified by the first derivative being zero and the slope changing from negative to positive or vice versa.
🔽 At a local minimum point, the graph is concave upward, and the first derivative changes from negative to positive.
🔼 At a local maximum point, the graph is concave downward, and the first derivative changes from positive to negative.
📊 The second derivative can be thought of as the slope of the first derivative, providing insight into the concavity of the function.
✅ A positive second derivative indicates the function is concave upward, while a negative second derivative indicates it is concave downward.
🤔 The video encourages viewers to think about the rate of change and how it relates to the slope and concavity, rather than just memorizing patterns.
📞 The speaker plans to cover inflection points in a future video and provide examples from calculus textbooks.
🎓 The ultimate goal is to provide a solid intuitive understanding of calculus that goes beyond just passing exams.

Q & A

What are the three types of interesting points typically found on the curves in a first semester calculus course?
-The three types of interesting points are maximum points, minimum points, and inflection points.
Why is it important to develop intuition for calculus concepts rather than just memorizing the rules?
-Developing intuition helps in long-term retention and application of the concepts, whereas memorization may lead to forgetting the rules after exams or over time.
How can you identify a local maximum point on a curve?
-A local maximum point can be identified where the slope of the curve is equal to 0, and it is the highest point in its surrounding neighborhood.
What is the significance of the first derivative being zero at interesting points on a curve?
-The first derivative being zero indicates that the slope of the curve at that point is 0, which is a characteristic of maximum, minimum, and inflection points.
What does the concavity of a graph tell us about the second derivative?
-If the second derivative is positive, the graph is concave upwards, and if it is negative, the graph is concave downwards. This provides insight into the shape of the graph and the behavior of the function at extrema points.
How does the slope of a tangent line to a curve change as you move from left to right on a graph that has a minimum point?
-The slope of the tangent line becomes less negative, reaches zero at the minimum point, and then becomes positive as you move further to the right.
What is the relationship between the first and second derivatives at a minimum point?
-At a minimum point, the first derivative is zero, and the second derivative is positive, indicating that the slope of the curve is increasing and the graph is concave upwards.
How does the graph of the second derivative look for a quadratic function like y = ax^2 + b?
-The graph of the second derivative for a quadratic function y = ax^2 + b is a constant line, since the derivative of 2ax is just 2a, which is a constant number.
What happens to the slope of the derivative as you move from left to right on a graph that has a maximum point?
-The slope of the derivative decreases from a high value, becomes 0 at the maximum point, and then continues to decrease, becoming more negative as you move further to the right.
How can you tell if a point on a curve is an inflection point?
-A point on a curve is an inflection point if the graph changes concavity at that point, but it is not a maximum or minimum point.
What will be covered in the next video after the one described in the transcript?
-The next video will provide intuition on inflection points and then proceed with examples from a calculus textbook.

Outlines

00:00

📚 Introduction to Calculus Concepts

The speaker begins by expressing their intention to create a series of videos covering fundamental calculus topics such as concavity, maxima, minima, and inflection points. They aim to provide a deeper understanding beyond just memorizing rules for exams. The speaker introduces the concept of three types of interesting points on curves typically encountered in first-semester calculus: points where the slope is zero, which correspond to local and global maxima and minima, as well as inflection points where the graph changes direction. They illustrate these points with a手绘 curve and explain that the slope of the tangent line at these points is what makes them significant in calculus. The speaker emphasizes the importance of understanding the behavior of the first and second derivatives at these points of interest.

05:02

📈 Analysis of Minimum and Maximum Points

In this section, the speaker delves deeper into the characteristics of minimum and maximum points on a curve, using the analogy of a parabola to explain these concepts. They discuss the behavior of the first derivative as it transitions from negative to positive, indicating a minimum point where the slope increases from negative to zero and then becomes positive. The speaker then introduces the concept of the second derivative, describing it as the 'slope of the slope' and explaining its role in determining whether a point is a minimum (concave up) or a maximum (concave down). They illustrate this with a hypothetical second-degree polynomial and describe how the second derivative would appear as a constant positive value in the case of a minimum. The speaker also touches on the behavior of the derivatives in the case of a maximum point, where the first derivative decreases from positive to zero and then becomes negative, and the second derivative is a constant negative value, indicating concavity downwards.

Mindmap

Keywords

💡Calculus

Calculus is a branch of mathematics that deals with the study of change and motion, primarily through the use of limits, derivatives, and integrals. In the context of the video, calculus is the subject of the course and the basis for discussing concepts such as concavity, maxima, minima, and inflection points.

💡Concavity

Concavity refers to the shape or curvature of a graph of a function. When a graph is concave up, it curves upward like a U-shape, and when it is concave down, it curves downward. In the video, the speaker aims to provide an intuitive understanding of concavity in relation to the second derivative being positive or negative.

💡Maxima and Minimum Points

Maxima and minimum points on a graph represent the highest and lowest points, respectively. A local maximum is a point that is higher than its immediate neighbors, while a local minimum is a point that is lower. A global maximum or minimum is the highest or lowest point on the entire graph. These points are significant in calculus as they indicate peaks and valleys on a curve.

💡Inflection Points

An inflection point on a graph is a point where the concavity changes, meaning the curve switches from concave up to concave down or vice versa. Unlike maxima and minima points, inflection points are not associated with a change in the magnitude of the function but rather a change in its curvature.

💡Derivatives

Derivatives in calculus represent the rate of change or the slope of a function at a particular point. The first derivative of a function gives the slope of the tangent line at any point on the graph of the function. Derivatives are crucial for analyzing the behavior of functions, such as finding maxima, minima, and inflection points.

💡Second Derivatives

The second derivative is the derivative of the first derivative. It provides information about the rate of change of the slope of a function, indicating whether the function is concave up or concave down. A positive second derivative indicates concavity upwards, while a negative second derivative indicates concavity downwards.

💡Slope

Slope refers to the steepness or gradient of a line, and in the context of a graph, it represents how quickly the function value (y) changes with respect to the independent variable (x). The slope is a fundamental concept in calculus for analyzing the behavior of functions, particularly at points of interest like maxima, minima, and inflection points.

💡Tangent Lines

Tangent lines are lines that touch a curve at a single point without crossing it. The slope of a tangent line at a particular point on a curve is equal to the derivative of the function at that point. Tangent lines are used to approximate the behavior of a function locally and to understand the instantaneous rate of change at that point.

💡Graphing

Graphing involves visually representing the relationship between variables using coordinates on a plane. In mathematics, it is a way to visualize functions and their properties, such as the shape of the curve, extrema points, and inflection points.

💡Extrema

Extrema are points on a graph where the function reaches a local maximum or minimum. These points are significant in calculus as they represent the turning points of a function, where the function changes from increasing to decreasing or vice versa.

Highlights

The speaker discusses the concept of concavity, maxima, minima, and inflection points in calculus.

The importance of understanding the intuition behind calculus concepts rather than just memorizing rules is emphasized.

The speaker introduces the idea that the interesting points on a curve often occur where the slope is equal to zero.

A local maximum and global maximum are differentiated, with the local maximum being a high point on a segment of the curve.

A local minimum and global minimum are explained, with the global minimum being the lowest point on the entire graph.

An inflection point is defined as a point on the curve where the graph changes direction but is neither a maximum nor a minimum.

The speaker provides a visual representation of a curve with maximum, minimum, and inflection points.

The relationship between the first derivative being zero and the slope of the curve is explored.

The concept of concavity and how it relates to the second derivative being positive or negative is discussed.

The speaker explains how the slope changes around a minimum point and how it indicates concavity.

The transition from a minimum to a maximum point is described, with the opposite behavior of the slope and concavity.

The speaker plans to cover inflection points in more detail in a future video.

The video aims to provide a deeper understanding of calculus concepts beyond just passing exams.

The speaker uses the example of y = ax^2 + b to illustrate the concepts of derivatives and concavity.

The video concludes with a promise to cover more examples and problems in future content.

Transcripts

Browse More Related Video

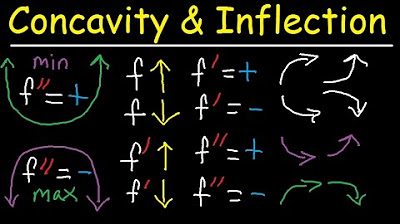
Concavity, Inflection Points, Increasing Decreasing, First & Second Derivative - Calculus

Using the Second Derivative (1 of 5: Finding the Point of Inflexion)

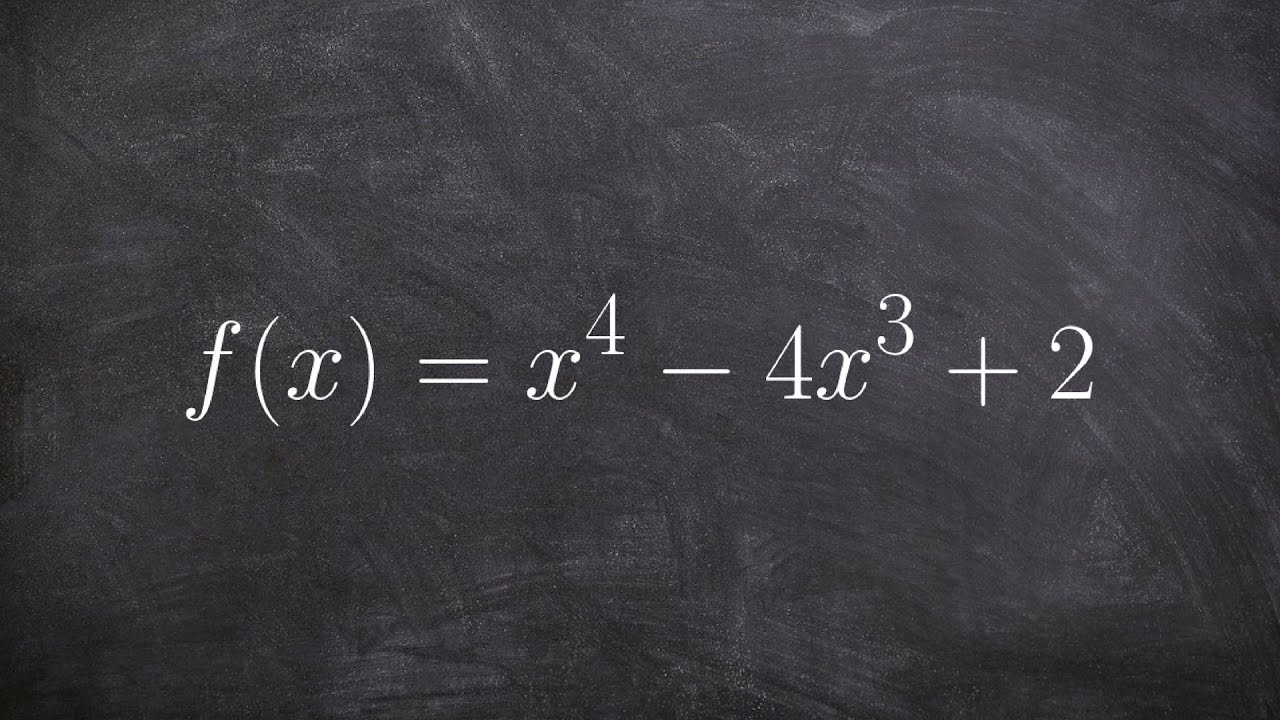
Learn how to determine concavity and point of inflection AP style

MATH1325 Lecture 10 2 - Concavity & Points of Inflection

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

Maxima Minima Slope Intuition

Takeaways

Q & A

What are the three types of interesting points typically found on the curves in a first semester calculus course?

Why is it important to develop intuition for calculus concepts rather than just memorizing the rules?

How can you identify a local maximum point on a curve?

What is the significance of the first derivative being zero at interesting points on a curve?

What does the concavity of a graph tell us about the second derivative?

How does the slope of a tangent line to a curve change as you move from left to right on a graph that has a minimum point?

What is the relationship between the first and second derivatives at a minimum point?

How does the graph of the second derivative look for a quadratic function like y = ax^2 + b?

What happens to the slope of the derivative as you move from left to right on a graph that has a maximum point?

How can you tell if a point on a curve is an inflection point?

What will be covered in the next video after the one described in the transcript?